Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T07:44:00.516Z Has data issue: false hasContentIssue false
  • English
  • Français

On a theory of laminar flow in channels of a certain class. II

Published online by Cambridge University Press:  24 October 2008

L. E. Fraenkel  and
P. M. Eagles
L. E. Fraenkel
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Cambridge
P. M. Eagles
Affiliation:
Mathematics Department, The City University, London
Get access Rights & Permissions [Opens in a new window]

Extract

This paper continues (and concludes) the mathematical analysis begun in (8) of a formal theory of viscous flow in channels with slowly curving walls. In that paper, the theory was shown to yield strict asymptotic expansions, in powers of the small curvature parameter, of exact solutions of the Navier-Stokes equations, but the proofs were restricted to a set 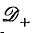of Reynolds numbers and wall divergence angles that is distinctly smaller than the set 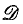on which the formal approximation is defined. In the present paper, we study in more detail a certain linear, partial differential operator TN, the invertibility of which is essential to the proofs. This operator is shown to be invertible (and the formal theory is thereby justified) on a parameter domain 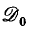that is much larger than 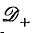and may well be the whole of 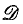. A key step is to associate with TN a family of operators that approximate TN locally and have much simpler coefficients.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 1 , January 1975 , pp. 199 - 224
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Betchov, R. and Criminale, W. O.Stability of parallel flows (Academic Press, 1967).Google Scholar
(2)Coddington, E. A. and Levinson, N.Theory of ordinary differential equations (McGraw-Hill, 1955).Google Scholar
(3)Davey, A. and Nguyen, H. P. F.Finite-amplitude stability of pipe flow. J. Fluid Mech. 45 (1971), 701–720.Google Scholar
(4)Eagles, P. M.The stability of a family of Jeffery-Hamel solutions for divergent channel flow. J. Fluid Mech. 24 (1966), 191–207.CrossRefGoogle Scholar
(5)Erdélyi, A.Asymptotic expansions (Dover, 1956).Google Scholar
(6)Fraenkel, L. E.Laminar flow in symmetrical channels with slightly curved walls. H. An asymptotic series for the stream function. Proc. Roy. Soc. Ser. A 272 (1963), 406–428.Google Scholar
(7)Fraenkel, L. E.On a class of linear partial differential equations with slowly varying coefficients. J. London Math. Soc. Ser. 2 5 (1972), 169–181.CrossRefGoogle Scholar
(8)Fraenkel, L. E.On a theory of laminar flow in channels of a certain class. Proc. Cambridge Philos. Soc. 73 (1973), 361–390.Google Scholar
(9)Reynolds, W. C. and Potter, M. C.Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27 (1967), 465–492.CrossRefGoogle Scholar
(10)Rudin, W.Functional analysis (McGraw-Hill, 1973).Google Scholar
(11)Taylor, A. E.Introduction to functional analysis (Wiley, 1958).Google Scholar
(12)Yosdia, H.Functional analysis (Springer, 1966).Google Scholar