Article contents
Adding propositional connectives to countable infinitary logic
Published online by Cambridge University Press: 24 October 2008
Abstract
For countable admissible α, one can add a new infinitary propositional connective to  so that the extended language obeys the Barwise compactness theorem, and the set of valid sentences is complete α-r.e.
so that the extended language obeys the Barwise compactness theorem, and the set of valid sentences is complete α-r.e.
Aside from obeying the compactness theorem and a completeness theorem, ordinary finitary predicate calculus is also truth-functionally complete.
In (1), Barwise shows that for countable admissible A, 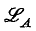 provides a fragment of
provides a fragment of 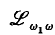 which obeys a compactness theorem and a completeness theorem. However, we of course lose truth-functional completeness, with respect to infinitary propositional connectives that operate on infinite sequences of propositional variables. This raises the question of studying extensions of the language
which obeys a compactness theorem and a completeness theorem. However, we of course lose truth-functional completeness, with respect to infinitary propositional connectives that operate on infinite sequences of propositional variables. This raises the question of studying extensions of the language 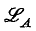 obtained by adding infinitary propositional connectives, in connexion with the Barwise compactness and completeness theorems, and other metatheorems, proved for
obtained by adding infinitary propositional connectives, in connexion with the Barwise compactness and completeness theorems, and other metatheorems, proved for 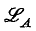 Some aspects of this project are proposed in (3). It is the purpose of this paper to answer a few of the more basic questions which arise in this connexion.
Some aspects of this project are proposed in (3). It is the purpose of this paper to answer a few of the more basic questions which arise in this connexion.
We have not attempted to study the preservation of interpolation or implicit definability. This could be quite interesting if done systematically.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 1 , January 1975 , pp. 1 - 6
- Copyright
- Copyright © Cambridge Philosophical Society 1975
References
REFERENCES
- 1
- Cited by


