Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T03:23:40.438Z Has data issue: false hasContentIssue false
  • English
  • Français

Cesàro iterations of Hausdorff matrices

Published online by Cambridge University Press:  24 October 2008

B. Kuttner
B. Kuttner
Affiliation:
University of Birmingham
Get access Rights & Permissions [Opens in a new window]

Extract

1. Jurkat and Peyerimhoff(3) (or see (4), pages 50–56) have given a definition of a function, f(A), of an infinite matrix A = (ank). In particular, they considered Aα, where a is any real constant. This is defined wherever A is normal; that is to say, when ank = 0 for k > n, and when, for all n, ann ±0. They also defined the ‘Cesàro iteration’ Aα. This is obtained by defining a matrix B = (bnn) by

(so that every diagonal element of B is 1), forming Bα, and then dividing each row by the row sum; that is to say, if Bα = (b(α)nk), we take

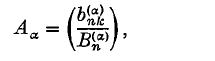
where

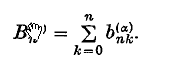
The definition requires, of course, that 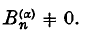≠ 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 1 , January 1975 , pp. 109 - 118
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Borwein, D.Theorems on some methods of summability. Quart. J. of Math. Oxford Ser. 2 9 (1958), 310–316.CrossRefGoogle Scholar
(2)Hardy, G. H.Divergent series (Oxford, 1949).Google Scholar
(3)Jurkat, W. and Peyerimaoff, A.Tuber Äquivalenzprobleme und andere Limitierungs theoretische Fragen bei Halbgruppen positiva Matrizen. Math. Ann. 159 (1965), 234–251.CrossRefGoogle Scholar
(4)Peyerimhoff, A.Lectures on Summability. (Lecture Notes in Mathematics, 107; Springér Verlag, 1969).CrossRefGoogle Scholar