Almost-conservative second-order differential equations
Published online by Cambridge University Press: 24 October 2008
Extract
During the last thirty years an immense amount of research has been done on differential equations of the form

where ε > 0 is small. It is usually assumed that the perturbing term on the right-hand side is a ‘good’ function of its arguments and that its dependence on t is purely trigonometric; this means that there is an expansion of the form
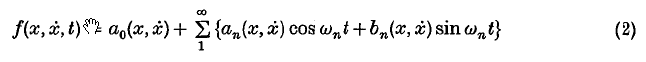
where the ωn are constants, and that one may impose any conditions on the rate of convergence of the series which turn out to be convenient. Without loss of generality we can assume
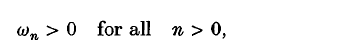
and for convenience we shall sometimes write ω0 = 0. Often f is assumed to be periodic in t, in which case it is implicit that the period is independent of x and ẋ (We can also allow f to depend on ε, provided it does so in a sensible manner.)
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 1 , January 1975 , pp. 159 - 169
- Copyright
- Copyright © Cambridge Philosophical Society 1975
References
REFERENCES
- 1
- Cited by


