The aim of the discrete logarithm problem with auxiliary inputs is to solve for  ${\it\alpha}$, given the elements
${\it\alpha}$, given the elements 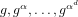 $g,g^{{\it\alpha}},\ldots ,g^{{\it\alpha}^{d}}$ of a cyclic group
$g,g^{{\it\alpha}},\ldots ,g^{{\it\alpha}^{d}}$ of a cyclic group 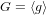 $G=\langle g\rangle$, of prime order
$G=\langle g\rangle$, of prime order  $p$. The best-known algorithm, proposed by Cheon in 2006, solves for
$p$. The best-known algorithm, proposed by Cheon in 2006, solves for  ${\it\alpha}$ in the case where
${\it\alpha}$ in the case where 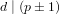 $d\mid (p\pm 1)$, with a running time of
$d\mid (p\pm 1)$, with a running time of 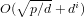 $O(\sqrt{p/d}+d^{i})$ group exponentiations (
$O(\sqrt{p/d}+d^{i})$ group exponentiations (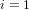 $i=1$ or
$i=1$ or 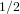 $1/2$ depending on the sign). There have been several attempts to generalize this algorithm to the case of
$1/2$ depending on the sign). There have been several attempts to generalize this algorithm to the case of 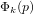 ${\rm\Phi}_{k}(p)$ where
${\rm\Phi}_{k}(p)$ where 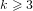 $k\geqslant 3$. However, it has been shown by Kim, Cheon and Lee that a better complexity cannot be achieved than that of the usual square root algorithms.
$k\geqslant 3$. However, it has been shown by Kim, Cheon and Lee that a better complexity cannot be achieved than that of the usual square root algorithms.
We propose a new algorithm for solving the DLPwAI. We show that this algorithm has a running time of 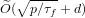 $\widetilde{O}(\sqrt{p/{\it\tau}_{f}}+d)$ group exponentiations, where
$\widetilde{O}(\sqrt{p/{\it\tau}_{f}}+d)$ group exponentiations, where 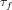 ${\it\tau}_{f}$ is the number of absolutely irreducible factors of
${\it\tau}_{f}$ is the number of absolutely irreducible factors of 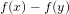 $f(x)-f(y)$. We note that this number is always smaller than
$f(x)-f(y)$. We note that this number is always smaller than 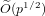 $\widetilde{O}(p^{1/2})$.
$\widetilde{O}(p^{1/2})$.
In addition, we present an analysis of a non-uniform birthday problem.
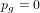 $p_{g}=0$,
$p_{g}=0$, 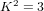 $K^{2}=3$ and 5-torsion
$K^{2}=3$ and 5-torsion
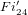 $Fi_{24}^{\prime }$ maximal
$Fi_{24}^{\prime }$ maximal  $2$-local geometry point-line collinearity graph
$2$-local geometry point-line collinearity graph
 $p$-adic analytic class number formula
$p$-adic analytic class number formula