Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T15:50:31.141Z Has data issue: false hasContentIssue false
  • English
  • Français

The linear programming relaxation permutation symmetry group of an orthogonal array defining integer linear program

Part of: Polytopes and polyhedra

Published online by Cambridge University Press:  01 June 2016

David M. Arquette  and
Dursun A. Bulutoglu
David M. Arquette
Affiliation:
Department of Mathematics and Statistics, Air Force Institute of Technology, Wright-Patterson Air Force Base, OH 45433, USA email [email protected]
Dursun A. Bulutoglu
Affiliation:
Department of Mathematics and Statistics, Air Force Institute of Technology, Wright-Patterson Air Force Base, OH 45433, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There is always a natural embedding of 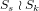$S_{s}\wr S_{k}$ into the linear programming (LP) relaxation permutation symmetry group of an orthogonal array integer linear programming (ILP) formulation with equality constraints. The point of this paper is to prove that in the $2$-level, strength-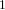$1$ case the LP relaxation permutation symmetry group of this formulation is isomorphic to 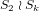$S_{2}\wr S_{k}$ for all $k$, and in the $2$-level, strength-$2$ case it is isomorphic to 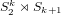$S_{2}^{k}\rtimes S_{k+1}$ for 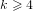$k\geqslant 4$. The strength-$2$ result reveals previously unknown permutation symmetries that cannot be captured by the natural embedding of 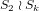$S_{2}\wr S_{k}$. We also conjecture a complete characterization of the LP relaxation permutation symmetry group of the ILP formulation.

Supplementary materials are available with this article.

MSC classification

Primary: 52B15: Symmetry properties of polytopes
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 206 - 216
Copyright
© 2016 U.S. Government under licence to the London Mathematical Society, with the exception of the United States of America where no copyright protection exists. 

References

Appa, G., Magos, D. and Mourtos, I., ‘On multi-index assignment polytopes’, Linear Algebra. Appl. 416 (2006) no. 23, 224–241, doi:10.1016/j.laa.2005.11.009.Google Scholar
Bulutoglu, D. and Margot, F., ‘Classification of orthogonal arrays by integer programming’, J. Statist. Plann. Inference 138 (2008) no. 3, 654–666.Google Scholar
Bulutoglu, D. and Ryan, K., ‘Integer programming for classifying orthogonal arrays’, Preprint, 2016,arXiv:1501.02281.Google Scholar
The GAP Group: ‘GAP—Groups, algorithms, and programming, version 4.6.4’, 2013,http://www.gap-system.org.Google Scholar
Geyer, A., ‘Different formulations of the orthogonal array problem and their symmetries’. PhD Thesis, Air Force Institute of Technology, OH, 2014.Google Scholar
Geyer, A., Bulutoglu, D. and Rosenberg, S., ‘The LP relaxation orthogonal array polytope and its permutation symmetries’, J. Combin. Math. Combin. Comput. 91 (2014) 165–176.Google Scholar
Liberti, L., ‘Reformulations in mathematical programming: automatic symmetry detection and exploitation’, Math. Program. 131 (2012) no. 1–2, 273–304.Google Scholar
Margot, F., ‘Exploiting orbits in symmetric ILP’, Math. Program. 98 (2003) no. 1–3, 3–21.Google Scholar
Margot, F., ‘Small covering designs by branch-and-cut’, Math. Program. 94 (2003) no. 2–3, 207–220.Google Scholar
Margot, F., ‘Symmetric ILP: coloring and small integers’, Discrete Optim. 4 (2007) no. 1, 40–62.Google Scholar
Margot, F., ‘Symmetry in integer linear programming’, 50 years of integer programming 1958–2008 (Springer, Heidelberg, 2010) 647–686.CrossRefGoogle Scholar
R Core Team, R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, 2013) http://www.R-project.org/.Google Scholar
Rosenberg, S., ‘A large index theorem for orthogonal arrays, with bounds’, Discrete Math. 137 (1995) no. 1, 315–318.Google Scholar
Rotman, J., An introduction to the theory of groups , 4th edn (Springer, New York, 1994).Google Scholar
Stufken, J. and Tang, B., ‘Complete enumeration of two-level orthogonal arrays of strength d with d + 2 constraints’, Ann. Statist. 35 (2007) no. 2, 793–814, doi:10.1214/009053606000001325.Google Scholar
Supplementary material: File

Arquette and Bulutoglu supplementary material

Arquette and Bulutoglu supplementary material 1

Download Arquette and Bulutoglu supplementary material(File)
File 48.5 KB