Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T08:57:36.766Z Has data issue: false hasContentIssue false
  • English
  • Français

A new approach to the discrete logarithm problem with auxiliary inputs

Part of: Theory of computing Computational number theory

Published online by Cambridge University Press:  01 January 2016

Jung Hee Cheon  and
Taechan Kim
Jung Hee Cheon
Affiliation:
Department of Mathematical Sciences, Seoul National University, GwanAkRo 1, Gwanak-Gu, Seoul 151-747, Korea email [email protected]
Taechan Kim
Affiliation:
NTT Secure Platform Laboratories, 3-9-11, Midori-cho, Musashino-Shi, Tokyo 180-8585, Japan email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of the discrete logarithm problem with auxiliary inputs is to solve for ${\it\alpha}$, given the elements 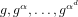$g,g^{{\it\alpha}},\ldots ,g^{{\it\alpha}^{d}}$ of a cyclic group 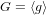$G=\langle g\rangle$, of prime order $p$. The best-known algorithm, proposed by Cheon in 2006, solves for ${\it\alpha}$ in the case where 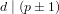$d\mid (p\pm 1)$, with a running time of 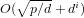$O(\sqrt{p/d}+d^{i})$ group exponentiations (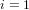$i=1$ or 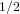$1/2$ depending on the sign). There have been several attempts to generalize this algorithm to the case of 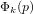${\rm\Phi}_{k}(p)$ where 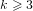$k\geqslant 3$. However, it has been shown by Kim, Cheon and Lee that a better complexity cannot be achieved than that of the usual square root algorithms.

We propose a new algorithm for solving the DLPwAI. We show that this algorithm has a running time of 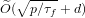$\widetilde{O}(\sqrt{p/{\it\tau}_{f}}+d)$ group exponentiations, where 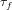${\it\tau}_{f}$ is the number of absolutely irreducible factors of 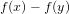$f(x)-f(y)$. We note that this number is always smaller than 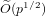$\widetilde{O}(p^{1/2})$.

In addition, we present an analysis of a non-uniform birthday problem.

MSC classification

Primary: 68Q25: Analysis of algorithms and problem complexity
Secondary: 11Y16: Algorithms; complexity
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 1 - 15
Copyright
© The Author(s) 2016 

References

Boneh, D. and Boyen, X., ‘Efficient selective-ID secure identity-based encryption without random oracles’, Advances in cryptology - EUROCRYPT 2004 , Lecture Notes in Computer Science 3027 (eds Cachin, C. and Camenisch, J.; Springer, Berlin, 2004) 223–238.Google Scholar
Boneh, D. and Boyen, X., ‘Short signatures without random oracles’, Advances in cryptology - EUROCRYPT 2004 , Lecture Notes in Computer Science 3027 (eds Cachin, C. and Camenisch, J.; Springer, Berlin, 2004) 56–73.Google Scholar
Boneh, D., Gentry, C. and Waters, B., ‘Collusion resistant broadcast encryption with short ciphertexts and private keys’, Advances in cryptology - CRYPTO 2005 , Lecture Notes in Computer Science 3621 (ed. Shoup, V.; Springer, Berlin, 2005) 258–275.Google Scholar
Brown, D. R. L. and Gallant, R. P., ‘The static Diffie–Hellman problem’, IACR Cryptology ePrint Archive (2004), http://eprint.iacr.org/2004/306.Google Scholar
Cheon, J. H., ‘Security analysis of the strong Diffie–Hellman problem’, Advances in cryptology - EUROCRYPT 2006 , Lecture Notes in Computer Science 4004 (ed. Vaudenay, S.; Springer, Berlin, 2006) 1–11.Google Scholar
Cheon, J. H., ‘Discrete logarithm problems with auxiliary inputs’, J. Cryptology 23 (2010) 457–476.Google Scholar
Cheon, J. H. and Kim, T., ‘Discrete logarithm with auxiliary inputs’, MSJ-KMS Joint Meeting 2012 (2012).Google Scholar
Cheon, J. H., Kim, T. and Song, Y. S., ‘A group action on z p × and the generalized DLP with auxiliary inputs’, Selected areas in cryptography 2013 , Lecture Notes in Computer Science 8282 (eds Lange, T., Lauter, K. E. and Lisonek, P.; Springer, Berlin, 2013) 121–135.Google Scholar
Galbraith, S. D. and Holmes, M., ‘A non-uniform birthday problem with applications to discrete logarithms’, Discrete Appl. Math. 160 (2012) 1547–1560.Google Scholar
Gomez-Calderon, J. and Madden, D. J., ‘Polynomials with small value set over finite fields’, J. Number Theory 28 (1988) 167–188.Google Scholar
Gomez-Calderon, J., ‘On the cardinality of value set of polynomials with coefficients in a finite field’, Proc. Japan Acad. Ser. A Math. Sci. 68 (1992) 338–340.Google Scholar
Gomez-Calderon, J., ‘The third-order factorable core of polynomials over finite fields’, Proc. Japan Acad. Ser. A Math. Sci. 74 (1998) 16–19.CrossRefGoogle Scholar
Hayes, D. R., ‘A geometric approach to permutation polynomials over a finite field’, Duke Math. J. 34 (1967) 293–305.Google Scholar
Kim, M., Cheon, J. H. and Lee, I.-S., ‘Analysis on a generalized algorithm for the strong discrete logarithm problem with auxiliary inputs’, Math. Comp. 83 (2014) 1993–2004.CrossRefGoogle Scholar
Mit’kin, D. A., ‘Polynomials with minimal set of values and the equation f (x) = f (y) in a finite prime field’, Mat. Zametki 38 (1985) 3–14.Google Scholar
Mitsunari, S., Sakai, R. and Kasahara, M., ‘A new traitor tracing’, IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E85-A (2002) 481–484.Google Scholar
Mohassel, P., ‘Fast computation on encrypted polynomials and applications’, CANS , Lecture Notes in Computer Science 7092 (eds Lin, D., Tsudik, G. and Wang, X.; Springer, 2011) 234–254.Google Scholar
Nishimura, K. and Sibuya, M., ‘Occupancy with two types of balls’, Ann. Inst. Statist. Math. 40 (1988) 77–91.Google Scholar
Pollard, J. M., ‘Monte Carlo methods for index computation (modp)’, Math. Comp. 32 (1978) 918–924.Google Scholar
Satoh, T., On generalization of Cheon’s algorithm, IACR Cryptology ePrint Archive (2009),http://eprint.iacr.org/2009/058.Google Scholar
Selivanov, B. I., ‘On waiting time in the scheme of random allocation of coloured particies’, Discrete Math. Appl. 5 (1955) 73–82.Google Scholar
Uchiyama, S., ‘Note on the mean value of v (f)’, Proc. Japan Acad. 31 (1955) 199–201.Google Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra (Cambridge University Press, Cambridge, 2003).Google Scholar
Weil, A., Sur les Courbes algébriques et les variétés qui s’en déduisent , Actualités Scientifiques et Industrielles 1041 (Hermann & Cie, 1948).Google Scholar