Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T02:00:17.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation of differential equations with non-monotone retarded arguments

Part of: Functional-differential and differential-difference equations

Published online by Cambridge University Press:  01 March 2016

George E. Chatzarakis  and
Özkan Öcalan
George E. Chatzarakis
Affiliation:
Department of Electrical and Electronic Engineering Educators, School of Pedagogical and Technological Education (ASPETE), N. Heraklion, 14121 Athens, Greece email [email protected]
Özkan Öcalan
Affiliation:
Akdeniz University, Faculty of Science, Department of Mathematics, 07058 Antalya, Turkey email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the first-order retarded differential equation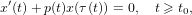

$$\begin{eqnarray}x^{\prime }(t)+p(t)x({\it\tau}(t))=0,\quad t\geqslant t_{0},\end{eqnarray}$$
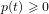where $p(t)\geqslant 0$ and 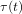${\it\tau}(t)$ is a function of positive real numbers such that 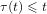${\it\tau}(t)\leqslant t$ for 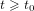$t\geqslant t_{0}$, and 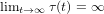$\lim _{t\rightarrow \infty }{\it\tau}(t)=\infty$. Under the assumption that the retarded argument is non-monotone, a new oscillation criterion, involving 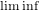$\liminf$, is established when the well-known oscillation condition
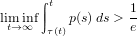$$\begin{eqnarray}\liminf _{t\rightarrow \infty }\int _{{\it\tau}(t)}^{t}p(s)\,ds>\frac{1}{e}\end{eqnarray}$$
 is not satisfied. An example illustrating the result is also given.

MSC classification

Primary: 34K11: Oscillation theory
Secondary: 34K06: Linear functional-differential equations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 98 - 104
Copyright
© The Author(s) 2016 

References

Arino, O., Győri, I. and Jawhari, A., ‘Oscillation criteria in delay equations’, J. Differential Equations 53 (1984) 115–123.Google Scholar
Berezansky, L. and Braverman, E., ‘On some constants for oscillation and stability of delay equations’, Proc. Amer. Math. Soc. 139 (2011) no. 11, 4017–4026.Google Scholar
Braverman, E. and Karpuz, B., ‘On oscillation of differential and difference equations with non-monotone delays’, Appl. Math. Comput. 218 (2011) 3880–3887.Google Scholar
Elbert, A. and Stavroulakis, I. P., ‘Oscillations of first order differential equations with deviating arguments, University of Ioannina T. R. No 172, 1990’, Recent trends in differential equations , World Scientific Series in Applicable Analysis 1 (World Scientific, River Edge, NJ, 1992) 163–178.Google Scholar
Elbert, A. and Stavroulakis, I. P., ‘Oscillation and non-oscillation criteria for delay differential equations’, Proc. Amer. Math. Soc. 123 (1995) 1503–1510.CrossRefGoogle Scholar
Erbe, L. H., Kong, Qingkai and Zhang, B. G., Oscillation theory for functional differential equations (Marcel Dekker, New York, 1995).Google Scholar
Erbe, L. H. and Zhang, B. G., ‘Oscillation of first order linear differential equations with deviating arguments’, Differential Integral Equations 1 (1988) 305–314.Google Scholar
Fukagai, N. and Kusano, T., ‘Oscillation theory of first order functional differential equations with deviating arguments’, Ann. Mat. Pura Appl. 136 (1984) 95–117.Google Scholar
Gopalsamy, K., Stability and oscillations in delay differential equations of population dynamics , Mathematics and its Applications 74 (Kluwer, Dordrecht, 1992).CrossRefGoogle Scholar
Grammatikopoulos, M. K., Koplatadze, R. G. and Stavroulakis, I. P., ‘On the oscillation of solutions of first order differential equations with retarded arguments’, Georgian Math. J. 10 (2003) 63–76.Google Scholar
Győri, I. and Ladas, G., Oscillation theory of delay differential equations with applications (Clarendon Press, Oxford, 1991).Google Scholar
Hunt, B. R. and Yorke, J. A., ‘When all solutions of x ′ =∑ q i (t)x (t − T i (t)) oscillate’, J. Differential Equations 53 (1984) 139–145.CrossRefGoogle Scholar
Koplatadze, R. G. and Chanturija, T. A., ‘Oscillating and monotone solutions of first-order differential equations with deviating arguments’, Differ. Uravn. 8 (1982) 1463–1465 (in Russian).Google Scholar
Ladas, G., ‘Sharp conditions for oscillations caused by delay’, Appl. Anal. 9 (1979) 93–98.Google Scholar
Ladas, G., Laskhmikantham, V. and Papadakis, J. S., ‘Oscillations of higher-order retarded differential equations generated by retarded arguments’, Delay and functional differential equations and their applications (Academic Press, New York, 1972) 219–231.Google Scholar
Ladde, G. S., Lakshmikantham, V. and Zhang, B. G., Oscillation theory of differential equations with deviating arguments , Monographs and Textbooks in Pure and Applied Mathematics 110 (Marcel Dekker, Inc., New York, 1987).Google Scholar
Myshkis, A. D., ‘Linear homogeneous differential equations of first order with deviating arguments’, Uspekhi Mat. Nauk 5 (1950) 160–162 (in Russian).Google Scholar
Tang, X. H., ‘Oscillation of first order delay differential equations with distributed delay’, J. Math. Anal. Appl. 289 (2004) 367–378.Google Scholar