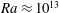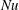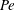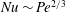JFM Papers
Experimental evidence of velocity profile inversion in developing laminar flow using magnetic resonance velocimetry
-
- Published online by Cambridge University Press:
- 25 July 2018, pp. 545-557
-
- Article
- Export citation
Surface and subsurface contributions to the build-up of forces on bed particles
-
- Published online by Cambridge University Press:
- 26 July 2018, pp. 558-572
-
- Article
- Export citation
Stability analysis of non-isothermal fibre spinning of polymeric solutions
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 573-605
-
- Article
- Export citation
Stokes flow of vesicles in a circular tube
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 606-635
-
- Article
- Export citation
Ageing and burst of surface bubbles
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 636-671
-
- Article
- Export citation
Exact third-order structure functions for two-dimensional turbulence
-
- Published online by Cambridge University Press:
- 30 July 2018, pp. 672-686
-
- Article
- Export citation
Flow around an inclined circular disk
-
- Published online by Cambridge University Press:
- 31 July 2018, pp. 687-714
-
- Article
- Export citation
Viscous constraints on microorganism approach and interaction
-
- Published online by Cambridge University Press:
- 31 July 2018, pp. 715-738
-
- Article
- Export citation
Erratum
Analytical theory of homogeneous mean shear turbulence – ERRATUM
-
- Published online by Cambridge University Press:
- 31 July 2018, p. 739
-
- Article
-
- You have access
- HTML
- Export citation
JFM Rapids
Streamwise self-similarity and log scaling in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 19 July 2018, R1
-
- Article
- Export citation
Axisymmetric simulation of viscoelastic filament thinning with the Oldroyd-B model
-
- Published online by Cambridge University Press:
- 18 July 2018, R2
-
- Article
- Export citation
Transition to ultimate Rayleigh–Bénard turbulence revealed through extended self-similarity scaling analysis of the temperature structure functions
-
- Published online by Cambridge University Press:
- 30 July 2018, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal heat transfer between two parallel plates
-
- Published online by Cambridge University Press:
- 31 July 2018, R4
-
- Article
- Export citation
On the origin of the circular hydraulic jump in a thin liquid film
-
- Published online by Cambridge University Press:
- 31 July 2018, R5
-
- Article
- Export citation
Vertically forced stably stratified cavity flow: instabilities of the basic state
-
- Published online by Cambridge University Press:
- 31 July 2018, R6
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 851 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 August 2018, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
FLM volume 851 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 August 2018, pp. b1-b5
-
- Article
-
- You have access
- Export citation