Article contents
Stokes flow of vesicles in a circular tube
Published online by Cambridge University Press: 30 July 2018
Abstract
The inertialess motion of lipid-bilayer vesicles flowing through a circular tube is investigated via direct numerical simulation and lubrication theory. A fully three-dimensional boundary integral equation method, previously used to study unbounded and wall-bounded Stokes flows around freely suspended vesicles, is extended to study the hindered mobility of vesicles through conduits of arbitrary cross-section. This study focuses on the motion of a periodic train of vesicles positioned concentrically inside a circular tube, with particular attention given to the effects of tube confinement, vesicle deformation and membrane bending elasticity. When the tube diameter is comparable to the transverse dimension of the vesicle, axisymmetric lubrication theory provides an approximate solution to the full Stokes-flow problem. By combining the present numerical results with a previously reported asymptotic theory (Barakat & Shaqfeh, J. Fluid Mech., vol. 835, 2018, pp. 721–761), useful correlations are developed for the vesicle velocity 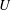 $U$ and extra pressure drop
$U$ and extra pressure drop 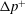 $\unicode[STIX]{x0394}p^{+}$. When bending elasticity is relatively weak, these correlations are solely functions of the geometry of the system (independent of the imposed flow rate). The prediction of Barakat & Shaqfeh (2018) supplies the correct limiting behaviour of
$\unicode[STIX]{x0394}p^{+}$. When bending elasticity is relatively weak, these correlations are solely functions of the geometry of the system (independent of the imposed flow rate). The prediction of Barakat & Shaqfeh (2018) supplies the correct limiting behaviour of 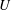 $U$ and
$U$ and 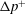 $\unicode[STIX]{x0394}p^{+}$ near maximal confinement, whereas the present study extends this result to all regimes of confinement. Vesicle–vesicle interactions, shape transitions induced by symmetry breaking, and unsteadiness introduce quantitative changes to
$\unicode[STIX]{x0394}p^{+}$ near maximal confinement, whereas the present study extends this result to all regimes of confinement. Vesicle–vesicle interactions, shape transitions induced by symmetry breaking, and unsteadiness introduce quantitative changes to 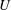 $U$ and
$U$ and 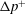 $\unicode[STIX]{x0394}p^{+}$. By contrast, membrane bending elasticity can qualitatively affect the hydrodynamics at sufficiently low flow rates. The dependence of
$\unicode[STIX]{x0394}p^{+}$. By contrast, membrane bending elasticity can qualitatively affect the hydrodynamics at sufficiently low flow rates. The dependence of 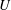 $U$ and
$U$ and 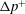 $\unicode[STIX]{x0394}p^{+}$ on the membrane bending stiffness (relative to a characteristic viscous stress scale) is found to be rather complex. In particular, the competition between viscous forces and bending forces can hinder or enhance the vesicle’s mobility, depending on the geometry and flow conditions.
$\unicode[STIX]{x0394}p^{+}$ on the membrane bending stiffness (relative to a characteristic viscous stress scale) is found to be rather complex. In particular, the competition between viscous forces and bending forces can hinder or enhance the vesicle’s mobility, depending on the geometry and flow conditions.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 11
- Cited by



