Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T09:18:23.999Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal heat transfer between two parallel plates

Published online by Cambridge University Press:  31 July 2018

Shingo Motoki Open the ORCID record for Shingo Motoki [Opens in a new window] ,
Genta Kawahara Open the ORCID record for Genta Kawahara [Opens in a new window]  and
Masaki Shimizu Open the ORCID record for Masaki Shimizu [Opens in a new window]
Shingo Motoki*
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560–8531, Japan
Genta Kawahara
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560–8531, Japan
Masaki Shimizu
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560–8531, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The divergence-free time-independent velocity field has been determined so as to maximise heat transfer between two parallel plates with a constant temperature difference under the constraint of fixed total enstrophy. The present variational problem is the same as that first formulated by Hassanzadeh et al. (J. Fluid Mech., vol. 751, 2014, pp. 627–662); however, the search range for optimal states has been extended to a three-dimensional velocity field. A scaling of the Nusselt number 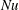$Nu$ with the Péclet number 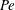$Pe$ (i.e., the square root of the non-dimensionalised enstrophy with thermal diffusion time scale), 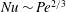$Nu\sim Pe^{2/3}$, has been found in the three-dimensional optimal states, corresponding to the asymptotic scaling with the Rayleigh number 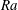$Ra$, 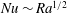$Nu\sim Ra^{1/2}$, expected to appear in an ultimate state, and thus to the Taylor energy dissipation law in high-Reynolds-number turbulence. At 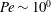$Pe\sim 10^{0}$, a two-dimensional array of large-scale convection rolls provides maximal heat transfer. A three-dimensional optimal solution emerges from bifurcation on the two-dimensional solution branch at 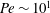$Pe\sim 10^{1}$, and the three-dimensional solution branch has been tracked up to 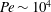$Pe\sim 10^{4}$ (corresponding to 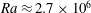$Ra\approx 2.7\times 10^{6}$). At 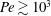$Pe\gtrsim 10^{3}$, the optimised velocity fields consist of convection cells with hierarchical self-similar vortical structures, and the temperature fields exhibit a logarithmic-like mean profile near the walls.

JFM classification

Flow Control: Mixing enhancement Mathematical Foundations: Variational methods
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , R4
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Bodenschatz, E. & He, X. 2014 Logarithmic temperature profiles of turbulent Rayleigh–Bénard convection in the classical and ultimate state for a Prandtl number of 0.8. J. Fluid Mech. 758, 436–467.Google Scholar
Busse, F. H. 1969 On Howard’s upper bound for heat transport by turbulent convection. J. Fluid Mech. 37, 457–477.Google Scholar
Doering, C. R. & Constantin, P. 1992 Energy dissipation in shear driven turbulence. Phys. Rev. Lett. 69, 1648–1651.Google Scholar
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53 (6), 5957–5981.Google Scholar
Doering, C. R., Otto, F. & Reznikoff, M. G. 2006 Bounds on vertical heat transport for infinite-Prandtl-number Rayleigh-Bénard convection. J. Fluid Mech. 560, 229–241.Google Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.Google Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.Google Scholar
Kerswell, R. R. 2001 New results in the variational approach to turbulent Boussinesq convection. Phys. Fluids 13, 192–209.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5 (11), 1374–1389.Google Scholar
Lohse, D. & Toschi, F. 2003 Ultimate state of thermal convection. Phys. Rev. Lett. 90, 034502.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Motoki, S., Kawahara, G. & Shimizu, M. 2018 Optimal heat transfer enhancement in plane Couette flow. J. Fluid Mech. 835, 1157–1198.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.Google Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background field. J. Fluid Mech. 477, 363–379.Google Scholar
Roche, P. E., Castaing, B., Chabaud, B. & Hébral, B. 2001 Observation of the 1/2 power law in Rayleigh–Bénard convection. Phys. Rev. E 63, 045303(R).Google Scholar
Souza, A. N.2016 An optimal control approach to bounding transport properties of thermal convection. PhD thesis, University of Michigan.Google Scholar
Tobasco, I. & Doering, C. R. 2017 Optimal wall-to-wall transport by incompressible flows. Phys. Rev. Lett. 118, 264502.Google Scholar
Whitehead, J. P. & Doering, C. R. 2011 Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106, 244501.Google Scholar
Whitehead, J. P. & Doering, C. R. 2012 Rigid bounds on heat transport by a fluid between slippery boundaries. J. Fluid Mech. 707, 241–259.Google Scholar
Zhu, X., Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2017 Roughness-facilitated local 1/2 scaling does not imply the onset of the ultimate regime of thermal convection. Phys. Rev. Lett. 119, 154501.Google Scholar