Article contents
Stability analysis of non-isothermal fibre spinning of polymeric solutions
Published online by Cambridge University Press: 30 July 2018
Abstract
The stability of fibre spinning flow of a polymeric fluid is analysed in the presence of thermal effects. The spinline is modelled as a one-dimensional slender-body filament of the entangled polymer solution. The previous study (Gupta & Chokshi, J. Fluid Mech., vol. 776, 2015, pp. 268–289) analysed linear and nonlinear stability behaviour of an isothermal extensional flow in the air gap during the fibre spinning process. The present study extends the analysis to take in to account the non-isothermal spinning flow in which the spinline loses heat by convection to the surrounding air as well as by solvent evaporation. The nonlinear rheology of the polymer solution is described using the eXtended Pom-Pom (XPP) model. The non-isothermal effects influence the rheology of the fluid through viscosity, which is taken to be temperature and concentration dependent. The linear stability analysis is carried out to obtain the draw ratio for the onset of instability, known as the draw resonance, and a stability diagram is constructed in the 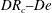 $DR_{c}{-}De$ plane.
$DR_{c}{-}De$ plane. 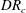 $DR_{c}$ is the critical draw ratio, and
$DR_{c}$ is the critical draw ratio, and 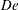 $De$ is the flow Deborah number. The enhancement in viscosity driven by spinline cooling leads to postponement in the onset of draw resonance, indicating the stabilising role of non-isothermal effects. Weakly nonlinear stability analysis is also performed to reveal the role of nonlinearities in the finite amplitude manifold in the vicinity of the flow transition point. For low to moderate Deborah numbers, the bifurcation is supercritical, and the flow attains an oscillatory state with an equilibrium amplitude post-transition when
$De$ is the flow Deborah number. The enhancement in viscosity driven by spinline cooling leads to postponement in the onset of draw resonance, indicating the stabilising role of non-isothermal effects. Weakly nonlinear stability analysis is also performed to reveal the role of nonlinearities in the finite amplitude manifold in the vicinity of the flow transition point. For low to moderate Deborah numbers, the bifurcation is supercritical, and the flow attains an oscillatory state with an equilibrium amplitude post-transition when 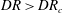 $DR>DR_{c}$. The equilibrium amplitude of the resonating state is found to be smaller when non-isothermal effects are incorporated in comparison to the isothermal spinning flow. For very fast flows in the regime of high Deborah numbers, the finite amplitude manifold crosses over to a subcritical state. In this limit, the nonlinearities render the flow unstable even in the linearly stable regime of
$DR>DR_{c}$. The equilibrium amplitude of the resonating state is found to be smaller when non-isothermal effects are incorporated in comparison to the isothermal spinning flow. For very fast flows in the regime of high Deborah numbers, the finite amplitude manifold crosses over to a subcritical state. In this limit, the nonlinearities render the flow unstable even in the linearly stable regime of 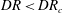 $DR<DR_{c}$.
$DR<DR_{c}$.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 8
- Cited by



