Thermoacoustic instabilities are one of the most challenging problems faced by gas turbine and rocket motor manufacturers. The key instability mechanism is described by the Rayleigh criterion. The Rayleigh criterion does not directly show how to alter a system to make it more stable. This is the objective of sensitivity analysis. Because thermoacoustic systems have many design parameters, adjoint sensitivity analysis has been proposed to obtain all the sensitivities with one extra calculation. Although adjoint sensitivity analysis can be carried out in both the time and the frequency domain, the frequency domain is more natural for a linear analysis. Perhaps surprisingly, the Rayleigh criterion has not yet been rigorously derived and comprehensively interpreted in the frequency domain. The contribution of this theoretical paper is threefold. First, the Rayleigh criterion is interpreted in the frequency domain with integral formulae for the complex eigenvalue. Second, the first variation of the Rayleigh criterion is calculated both in the time and frequency domain, both with and without Lagrange multipliers (adjoint variables). The Lagrange multipliers are physically related to the system’s observables. Third, an adjoint Rayleigh criterion is proposed. The paper also points out that the conclusions of Juniper (Phys. Rev. Fluids, vol. 3, 2018, 110509) apply to the first variation of the Rayleigh criterion, not to the Rayleigh criterion itself. The mathematical relations of this paper can be used to compute sensitivities directly from measurable quantities to enable optimal design.

We report laboratory experiments of long-crested irregular water surface waves propagating over a shoal. For a sufficiently shallow shoal we find that the surface elevation can have a local maximum of skewness and kurtosis above the shallower part of the shoal close to the edge on the incoming side, and a local minimum of skewness over the downward slope on the lee side of the shoal. We find that the horizontal fluid velocity can have a local maximum and minimum of skewness at the same locations as those for the surface elevation. However, the kurtosis of the horizontal fluid velocity can have a local maximum over the downward slope on the lee side of the shoal, different from the location of the maximum of kurtosis of the surface elevation.

How a drop spreads across a solid surface is crucial to many applications in science and engineering. Yet, there is much we still do not understand about this phenomenon. In particular, situations where the edge of the drop moves rapidly across the surface remain obscure. There are two main issues: the effect of inertia and the presence of defects that are always present on ordinary surfaces and hinder the advancement of the liquid. Sartori et al. (J. Fluid Mech., vol. 876, 2019) show how these effects can be separated in the case of climbing drops, a phenomenon where drops paradoxically climb an inclined vibrating plate.

We consider a Stokeslet applied to a viscous fluid next to an infinite, flat wall, or in between two parallel walls. We calculate the forces exerted by the resulting flow on the confining boundaries, and use the results obtained to estimate the hydrodynamic contribution to the pressure exerted on boundaries by force-free self-propelled particles.

Turbulent flows in the presence of walls may be apprehended as a collection of momentum- and energy-containing eddies (energy-eddies), whose sizes differ by many orders of magnitude. These eddies follow a self-sustaining cycle, i.e. existing eddies are seeds for the inception of new ones, and so forth. Understanding this process is critical for the modelling and control of geophysical and industrial flows, in which a non-negligible fraction of the energy is dissipated by turbulence in the immediate vicinity of walls. In this study, we examine the causal interactions of energy-eddies in wall-bounded turbulence by quantifying how the knowledge of the past states of eddies reduces the uncertainty of their future states. The analysis is performed via direct numerical simulation of turbulent channel flows in which time-resolved energy-eddies are isolated at a prescribed scale. Our approach unveils, in a simple manner, that causality of energy-eddies in the buffer and logarithmic layers is similar and independent of the eddy size. We further show an example of how novel flow control and modelling strategies can take advantage of such self-similar causality.

By means of three-dimensional direct numerical simulations, we investigate the influence of the regular roughness of heated and cooled plates on the mean heat transport in a cylindrical Rayleigh–Bénard convection cell of aspect ratio one. The roughness is introduced by a set of isothermal obstacles, which are attached to the plates and have a form of concentric rings of the same width. The considered Prandtl number 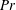$Pr$ equals 1, the Rayleigh number 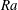$Ra$ varies from 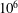$10^{6}$ to 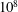$10^{8}$, the number of rings on each plate is 1, 2, 4, 8 or 10, the height of the rings is varied from 1.5 % to 49 % of the cylinder height and the gap between the rings is varied from 1.5 % to 18.8 % of the cell diameter. Totally, 135 different cases are analysed. Direct numerical simulations show that with small 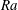$Ra$ and wide roughness rings, a small reduction of the mean heat transport (the Nusselt number 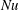$Nu$) is possible, but, in most cases, the presence of the heated and cooled obstacles generally leads to an increase of 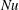$Nu$, compared to the case of classical Rayleigh–Bénard convection with smooth plates. When the rings are very tall and the gaps between them are sufficiently wide, the effective mean heat flux can be several times larger than in the smooth case. For a fixed geometry of the obstacles, the scaling exponent in the 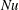$Nu$ versus 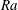$Ra$ scaling first increases with growing 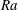$Ra$ up to approximately 0.5, but then smoothly decreases back towards the exponent in the no-obstacle case.

We present simultaneous two-dimensional measurements of the velocity and buoyancy fields on a central vertical plane in two-dimensional line plumes: a free plume distant from vertical boundaries and a wall plume, adjacent to a vertical wall. Data are presented in both an Eulerian and a plume coordinate system that follow the instantaneous turbulent/non-turbulent interface (TNTI) of the plume. We present measurements in both coordinate systems and compare the entrainment in the two flows. We find that the value of the entrainment coefficient in the wall plume is greater than half that of the free plume. The reduction in entrainment is investigated by considering a decomposition of the entrainment coefficient based on the mean kinetic energy where the relative contributions of turbulent production, buoyancy and viscous terms are calculated. The reduced entrainment is also investigated by considering the statistics of the TNTI and the conditional vertical transport of the ambient and engulfed fluid. We show that the wall shear stress is non-negligible and that the free plume exhibits significant meandering. The effect of the meandering on the entrainment process is quantified in terms of the stretching of the TNTI where it is shown that the length of the TNTI is greater in the free plume and, further, the relative vertical transport of the engulfed ambient fluid is observed to be 15 % greater in the free plume. Finally, the turbulent velocity and buoyancy fluctuations, Reynolds stresses and the turbulent buoyancy fluxes are presented in both coordinate systems.

We present a numerical study on the rheology of semi-dilute and concentrated filament suspensions of different bending stiffness and Reynolds number, with the immersed boundary method used to couple the fluid and solid. The filaments are considered as one-dimensional inextensible slender bodies with fixed aspect ratio, obeying the Euler–Bernoulli beam equation. To understand the global suspension behaviour we relate it to the filament microstructure, deformation and elastic energy and examine the stress budget to quantify the effect of the elastic contribution. At fixed volume fraction, the viscosity of the suspension reduces when decreasing the bending rigidity and grows when increasing the Reynolds number. The change in the relative viscosity is stronger at finite inertia, although still in the laminar flow regime, as considered here. Moreover, we find the first normal stress difference to be positive as in polymeric fluids, and to increase with the Reynolds number; its value has a peak for an intermediate value of the filament bending stiffness. The peak value is found to be proportional to the Reynolds number, moving towards more rigid suspensions at larger inertia. Moreover, the viscosity increases when increasing the filament volume fraction, and the rate of increase of the filament stress with the bending rigidity is stronger at higher Reynolds numbers and reduces with the volume fraction. We show that this behaviour is associated with the formation of a more ordered structure in the flow, where filaments tend to be more aligned and move as a compact aggregate, thus reducing the filament–filament interactions despite their volume fraction increases.

We analyse how a succession of single bubbles extracts dissolved gas from a liquid solution while they grow and detach in a confinement induced by the presence of lateral walls. Like bubbles growing on a liquid-immersed unconfined surface, these bubbles absorb the dissolved gas in the liquid around them and hence deplete their surroundings. The supersaturation level, $\unicode[STIX]{x1D701}$, stands out as the main parameter which determines the diffusive bubble dynamics, both in the confined and unconfined scenarios. For slightly supersaturated solutions, the bubble evolution is rather similar for the two cases. We observe nonetheless mildly higher concentration gradients within confinement due to the lack of gas renewal. This causes a slightly enhancement of density-driven convection as compared to the unconfined case, which results in a higher mass transfer rate towards the bubble and a somewhat faster long-term gas depletion. For larger supersaturations, the onset of natural convection is inhibited by the presence of the confinement. Confinement promotes the gas mixing within the cavity as well. These two effects combined result in a slower depletion in the confined case as compared to the unconfined one. The two opposite behaviours for small and large supersaturation suggest that there must be a transition in between the two scenarios. The cross-over has been estimated to occur at $\unicode[STIX]{x1D701}\approx 0.17$. We propose a modified depletion model which accounts for the confined configuration and its effect on the effective area through which gas diffuses into the bubble. The model can accurately describe the experimental results and sheds more light on the origin of the depletion effect due to the successive bubble growth.

It is well known that a rigid non-slippery particle in unsteady motion can experience a Basset history force with the signature $1/\unicode[STIX]{x1D6FF}$ decay due to a Stokes boundary layer of thickness $\unicode[STIX]{x1D6FF}$. For a uniform slip particle with slip length $\unicode[STIX]{x1D706}$, however, a persistent force plateau can replace the usual Basset decay at $\unicode[STIX]{x1D6FF}$ below the slip–stick transition (SST) point $\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D706}$ (Premlata & Wei, J. Fluid Mech., vol. 866, 2019, pp. 431–449). Here we analyse the hydrodynamic force on an oscillating stick–slip Janus particle, showing that it can display unusual history force responses that are of neither the no-slip nor the purely slip type but mixed with both. Solving the oscillatory Stokes flow equation together with a matched asymptotic boundary layer theory, we find that the persistent force plateau seen for a uniform slip particle may be destroyed by the presence of the stick portion of a stick–slip Janus particle. Instead, a $1/\unicode[STIX]{x1D6FF}$ Basset force of amplitude smaller than the no-slip counterpart will re-emerge to dominate the high frequency viscous force response again. This re-entry Basset force, which occurs only after making a stick patch on a slippery particle, is also found to depend solely on the coverage of the stick face irrespective of the slip length of the slip face. When the stick portion is small, in particular, the re-entry Basset decay will exhibit a slip plateau on its tail, displaying a distinctive re-entrant history force transition prior to the SST. But if changing this tiny stick face to be slippery, no matter how small the slip length is, the re-entry Basset decay will disappear and a constant force plateau will return to dominate the force response again. These unusual force responses arising from mixed stick–slip or non-uniform slip effects may not only provide unique hydrodynamic fingerprints for characterizing heterogeneous particles, but also have potential uses in active manipulation and sorting of these particles.

Survival of entropy waves during their advection throughout a combustor is central to the generation of entropic sound and the subsequent effects upon thermoacoustic stability of the system. However, the decay and spatial non-uniformity of entropy waves are largely ignored by the existing models used for the calculation of entropy noise generation. Recent investigations have demonstrated the complex spatio-temporal dynamics of entropy waves and cast doubts on the sufficiency of the one-dimensional approach, conventionally used for the analysis of these waves. Hence, this paper proposes a novel approach to the low-order modelling of entropy wave evolution wherein the wave is described by the two states of position and amplitude in the streamwise direction. A high-order model is first developed through direct numerical simulation of the advection of entropy waves in a fully developed, heat transferring, compressible, turbulent channel flow. The data are then utilised to build and validate a series of nonlinear, low-order models that provide an unsteady two-dimensional representation of the decaying and partially annihilating entropy waves. It is shown that these models need, at most, approximately $12.5\,\%$ of the total trace of entropy wave advection to predict the wave dynamics accurately. The results further reveal that the existing linear low-order models are truly predictive only for the entropy waves with less than $2\,\%$ increase in the gas temperature compared to that of the surrounding flow. Yet, in agreement with the assumption of existing models, it is shown that entropy waves travel with the mean flow speed.

The gravitationally driven flow of fluid from a reservoir following the partial collapse of its confining dam, or the partial opening of its confining lock, is modelled using the nonlinear shallow water equations, coupled to outflow conditions, in which the drainage is modelled as flow over a constricted, broad-crested weir. The resulting unsteady motion reveals systematic draining, on which strong and relatively rapid oscillations are imposed. The oscillations propagate between the outflow and the impermeable back wall of the reservoir. This dynamics is investigated utilising three methods: hodograph techniques to yield quasi-analytical solutions, asymptotic analysis at relatively late times after initiation and numerical integration of the governing equations. The hodograph transformation is used to find exact solutions at early times, revealing that from initially quiescent conditions the fluid drains and yet repeatedly generates intervals during which there are regions of constant depth and velocity adjacent to the boundaries. A novel modified multiscale asymptotic analysis designed for late times is employed to determine the limiting rate of draining and wave structure. It is shown that the excess height drains as $t^{-2}$ and, when the obstacle has finite height, the velocity field decays as $t^{-3}$, and exhibits a wave structure that tends towards a constant and relatively rapid phase speed. In the case of a pure constriction, for which all the fluid ultimately drains out of the reservoir, the motion adjusts to a self-similar state in which the velocity field decays as $t^{-1}$. Oscillations around this state have an exponentially increasing period. Numerical simulations with a novel implementation of boundary conditions are performed; they confirm the hodograph solution and provide data for the asymptotic results.

We examine how known unstable equilibria of the Navier–Stokes equations in plane Couette flow adapt to the presence of an imposed stable density difference between the two boundaries for varying values of the Prandtl number $Pr$, the ratio of viscosity to density diffusivity and fixed moderate Reynolds number, $Re=400$. In the two asymptotic limits $Pr\rightarrow 0$ and $Pr\rightarrow \infty$, it is found that such solutions exist at arbitrarily high bulk stratification but for different physical reasons. In the $Pr\rightarrow 0$ limit, density variations away from a constant stable density gradient become vanishingly small as diffusion of density dominates over advection, allowing equilibria to exist for bulk Richardson number $\mathit{Ri}_{b}\lesssim O(Re^{-2}Pr^{-1})$. Alternatively, at high Prandtl numbers, density becomes homogenised in the interior by the dominant advection which creates strongly stable stratified boundary layers that recede into the wall as $Pr\rightarrow \infty$. In this scenario, the density stratification and the flow essentially decouple, thereby mitigating the effect of increasing $\mathit{Ri}_{b}$. An asymptotic analysis is presented in the passive scalar regime $\mathit{Ri}_{b}\lesssim O(Re^{-2})$, which reveals $O(Pr^{-1/3})$-thick stratified boundary layers with $O(Pr^{-2/9})$-wide eruptions, giving rise to density fingers of $O(Pr^{-1/9})$ length and $O(Pr^{-4/9})$ width that invade an otherwise homogeneous interior. Finally, increasing $Re$ to $10^{5}$ in this regime reveals that interior stably stratified density layers can form away from the boundaries, separating well-mixed regions.

Three related problems of viscoplastic flow around cylinders are considered. First, translating cylinders with no-slip surfaces appear to generate adjacent rotating plugs in the limit where the translation speed becomes vanishingly small. In this plastic limit, analytical results are available from plasticity theory (slipline theory) which indicate that no such plugs should exist. Using a combination of numerical computations and asymptotic analysis, we show that the plugs of the viscoplastic theory actually disappear in the plastic limit, albeit very slowly. Second, when the boundary condition on the cylinder is replaced by one that permits sliding, the plastic limit corresponds to a partially rough cylinder. In this case, no plasticity solution has been previously established; we provide evidence from numerical computations and slipline theory that a previously proposed upper bound (Martin & Randolph, Geotechnique, vol. 56, 2006, pp. 141–145) is actually the true plastic solution. Third, we consider how a prescribed surface velocity field can propel cylindrical squirmers through a viscoplastic fluid. We determine swimming speeds and contrast the results with those from the corresponding Newtonian problem.

Flows in the close proximity of the vapour–liquid saturation curve and critical point are examined for supersonic turbine cascades, where an expansion occurs through a converging–diverging blade channel. The present study illustrates potential advantages and drawbacks if turbine blades are designed for operating conditions featuring a non-monotonic variation of the Mach number through the expansion process, and non-ideal oblique shocks and Prandtl–Meyer waves downstream of the trailing edge. In contrast to ideal-gas flows, for a given pressure ratio across the cascade, the flow field and the turbine performance are found to be highly dependent on the thermodynamic state at the turbine inlet, in both design and off-design conditions. A potentially advantageous design, featuring stationary points of the Mach number at the blade trailing edge, is proposed, which induces a nearly uniform outlet Mach number distribution in the stator–rotor gap with a low sensitivity to slight variations in the outlet pressure. These findings are relevant for turbomachines involved in high-temperature organic Rankine cycle power systems, in particular for supercritical applications.

We present a new nonlinear mode decomposition method to visualize decomposed flow fields, named the mode decomposing convolutional neural network autoencoder (MD-CNN-AE). The proposed method is applied to a flow around a circular cylinder at the Reynolds number $Re_{D}=100$ as a test case. The flow attributes are mapped into two modes in the latent space and then these two modes are visualized in the physical space. Because the MD-CNN-AEs with nonlinear activation functions show lower reconstruction errors than the proper orthogonal decomposition (POD), the nonlinearity contained in the activation function is considered the key to improving the capability of the model. It is found by applying POD to each field decomposed using the MD-CNN-AE with hyperbolic tangent activation such that a single nonlinear MD-CNN-AE mode contains multiple orthogonal bases, in contrast to the linear methods, i.e. POD and MD-CNN-AE with linear activation. We further assess the proposed MD-CNN-AE by applying it to a transient process of a circular cylinder wake in order to examine its capability for flows containing high-order spatial modes. The present results suggest a great potential for the nonlinear MD-CNN-AE to be used for feature extraction of flow fields in lower dimensions than POD, while retaining interpretable relationships with the conventional POD modes.

This study explores the control of mesoscale variability by topographic features with lateral scales that are less than the scale of the eddies generated by baroclinic instability. These dynamics are described using a combination of numerical simulations and an asymptotic multiscale model. The multiscale method makes it possible to express the system dynamics by a closed set of equations written entirely in terms of mesoscale variables, thereby providing a physical basis for the development of submesoscale parameterization schemes. The submesoscale topography is shown to influence such fundamental properties of mesoscale variability as the meridional eddy-induced transport and eddy kinetic energy. It is argued that the adverse influence of submesoscale topography on baroclinic instability is ultimately caused by the homogenization tendency of potential vorticity in the bottom density layer. The multiscale model formally assumes a substantial separation between the scales of interacting flow components. However, the comparison of asymptotic solutions with their submesoscale-resolving numerical counterparts indicates that the multiscale method is remarkably accurate even when scale separation is virtually non-existent.

Laboratory measurements of velocity fields and void fraction under spilling breaking waves are presented. Modified particle image velocimetry was used to quantify the flow kinematics and turbulence while fibre optic reflectometry was used to quantify the breaking-induced air entrainment inside the aerated region of the spilling breakers. The measurements confirmed that the ratio of the local energy flux and the local energy density sharply increases and exceeds the threshold value of 0.85 near the onset of breaking. Based on the measured velocity fields, the maximum horizontal velocity reached $1.1C$ at the onset of breaking, with $C$ being the phase speed of the primary breaking wave. The maximum horizontal velocity then reached $1.5C$ at approximately one-quarter of a wave period after the onset of breaking. The results also confirmed that the wavelet-educed turbulence length scale estimates are comparable to the previously reported values with different wave parameters, suggesting that the dependence of the size of energy-containing eddies on the physical scales of the breaking waves is insignificant. The measured void fraction showed a similarity profile although the measurement locations span one wavelength. The mean kinetic energy, turbulent kinetic energy, potential energy and total energy were quantified with and without the void fraction being accounted for. Results show near 60 % and 40 % overestimates of the kinetic energy and the potential energy if the void fraction is not considered. After correcting the density variation due to air entrainment, the total energy dissipated following an exponential decay, with 43 % and 65 % energy being dissipated at one and two wavelengths downstream from the breaking point, respectively. The equipartition assumption was found to be applicable before and during the entire breaking process in the present spilling breakers.

We present a method to incorporate weakly nonlinear ageostrophic corrections into a previously developed wave–vortex decomposition algorithm for one-dimensional data obtained along horizontal flight, ship or remote-sensing tracks in the atmosphere or ocean. A new statistical omega equation is derived that links the power spectra of a quasi-geostrophic stream function to the power spectra of the ageostrophic correction. This step assumes mutually independent Fourier components for the quasi-geostrophic stream function. Then this equation is used to estimate the ageostrophic correction from one-dimensional track data under the additional assumptions of horizontal isotropy and the dominance of a single vertical wavenumber scale. A robust and accurate numerical method is designed, tested successfully against synthetic data and then applied to atmospheric flight track data near the tropopause. This probes the robustness of the previous linear wave–vortex decomposition method under the ageostrophic corrections. Preliminary findings indicate that the lower stratospheric flight tracks are very robust whilst the upper tropospheric ones showed some sensitivity to the correction.

We consider pairs of self-similar two-dimensional vortex sheets forming cusps, equivalently single sheets merging into slip condition walls, as in classical Mach reflection at wedges. We derive from the Birkhoff–Rott equation a reduced model yielding formulas for cusp exponents and other quantities as functions of the similarity exponent and strain coefficient. Comparison to numerics shows that the piecewise quadratic and higher approximation of vortex sheets agree with each other and with the model. In contrast, piecewise linear schemes produce spurious results and violate conservation of mass, a problem that may have been undetected in prior work for other vortical flows. We find that vortex cusps only exist if the similarity exponent is sufficiently large and if the circulation on the sheet is counterclockwise (for a sheet above the wall with cusp opening to the right), unless a sufficiently positive strain coefficient compensates. Whenever a cusp cannot exist a spiral-ended jet forms instead; we find many jets are so narrow that they appear as false cusps.