Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T04:10:13.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Stably stratified exact coherent structures in shear flow: the effect of Prandtl number

Published online by Cambridge University Press:  06 November 2019

Jake Langham Open the ORCID record for Jake Langham [Opens in a new window] ,
Tom S. Eaves Open the ORCID record for Tom S. Eaves [Opens in a new window]  and
Rich R. Kerswell
Jake Langham*
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK
Tom S. Eaves
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Rd., Vancouver BC V6T 1Z2, Canada
Rich R. Kerswell
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1TW, UK Centre for Mathematical Sciences, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

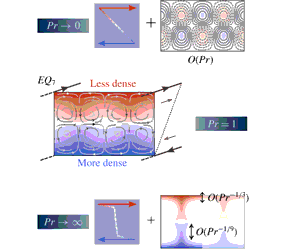
We examine how known unstable equilibria of the Navier–Stokes equations in plane Couette flow adapt to the presence of an imposed stable density difference between the two boundaries for varying values of the Prandtl number $Pr$, the ratio of viscosity to density diffusivity and fixed moderate Reynolds number, $Re=400$. In the two asymptotic limits $Pr\rightarrow 0$ and $Pr\rightarrow \infty$, it is found that such solutions exist at arbitrarily high bulk stratification but for different physical reasons. In the $Pr\rightarrow 0$ limit, density variations away from a constant stable density gradient become vanishingly small as diffusion of density dominates over advection, allowing equilibria to exist for bulk Richardson number $\mathit{Ri}_{b}\lesssim O(Re^{-2}Pr^{-1})$. Alternatively, at high Prandtl numbers, density becomes homogenised in the interior by the dominant advection which creates strongly stable stratified boundary layers that recede into the wall as $Pr\rightarrow \infty$. In this scenario, the density stratification and the flow essentially decouple, thereby mitigating the effect of increasing $\mathit{Ri}_{b}$. An asymptotic analysis is presented in the passive scalar regime $\mathit{Ri}_{b}\lesssim O(Re^{-2})$, which reveals $O(Pr^{-1/3})$-thick stratified boundary layers with $O(Pr^{-2/9})$-wide eruptions, giving rise to density fingers of $O(Pr^{-1/9})$ length and $O(Pr^{-4/9})$ width that invade an otherwise homogeneous interior. Finally, increasing $Re$ to $10^{5}$ in this regime reveals that interior stably stratified density layers can form away from the boundaries, separating well-mixed regions.

JFM classification

Turbulent Flows: Stratified turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A10
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Budanur, N. B., Short, K. Y., Farazmand, M., Willis, A. P. & Cvitanović, P. 2017 Relative periodic orbits form the backbone of turbulent pipe flow. J. Fluid Mech. 833, 274–301.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.Google Scholar
Childress, S. 1979 Alpha-effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20, 172–180.Google Scholar
Childress, S. & Gilbert, A. D. 1995 Stretch, Twist and Fold: The Fast Dynamo, vol. 37. Springer.Google Scholar
Cvitanović, P. & Gibson, J. F. 2010 Geometry of the turbulence in wall-bounded shear flows: periodic orbits. Phys. Scr. 2010 (T142), 014007.Google Scholar
Deguchi, K. 2017 Scaling of small vortices in stably stratified shear flows. J. Fluid Mech. 821, 582–594.Google Scholar
Deguchi, K. & Walton, A. G. 2013 A swirling spiral wave solution in pipe flow. J. Fluid Mech. 737, R2.Google Scholar
Duguet, Y., Brandt, L. & Larsson, B. R. J. 2010 Towards minimal perturbations in transitional plane Couette flow. Phys. Rev. E 82 (2), 026316.Google Scholar
Eaves, T. S. & Caulfield, C. P. 2015 Disruption of SSP/VWI states by a stable stratification. J. Fluid Mech. 784, 548–564.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Garaud, P., Gagnier, D. & Verhoeven, J. 2017 Turbulent transport by diffusive stratified shear flows: from local to global models. I. Numerical simulations of a stratified plane Couette flow. Astrophys. J. 837 (2), 133–147.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Gibson, J. F., Reetz, F., Azimi, S., Ferraro, A., Kreilos, T., Schrobsdorff, H., Farano, M., Yesil, A. F., Schütz, S. S., Culpo, M. et al. 2019 Channelflow 2.0. (in preparation), see https://www.channelflow.ch.Google Scholar
Gregg, M. C. 1980 Microstructure patches in the thermocline. J. Phys. Oceanogr. 10 (6), 915–943.Google Scholar
Hall, P. 2012 Vortex–wave interactions/self-sustained processes in high Prandtl number natural convection in a vertical channel with moving sidewalls. Stud. Appl. Maths 129 (1), 1–25.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Holford, J. M. & Linden, P. F. 1999 Turbulent mixing in a stratified fluid. Dyn. Atmos. Oceans 30, 173–198.Google Scholar
Itano, T. & Generalis, S. C. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Lett. 102 (11), 114501.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70 (3), 703–716.Google Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Transfer 24 (9), 1541–1544.Google Scholar
Kawahara, G., Uhlmann, M. & Van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.Google Scholar
Kerswell, R. R. 2005 Recent progress in understanding the transition to turbulence in a pipe. Nonlinearity 18 (6), R17.Google Scholar
Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Lignières, F. 1999 The small-Péclet-number approximation in stellar radiative zones. Astron. Astrophys. 248, 933–939.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Gephys. Astrophys. Fluid Dyn. 13, 3–23.Google Scholar
Lucas, D. & Caulfield, C. P. 2017 Irreversible mixing by unstable periodic orbits in buoyancy dominated stratified turbulence. J. Fluid Mech. 832, R1.Google Scholar
Lucas, D., Caulfield, C. P. & Kerswell, R. R. 2017 Layer formation in horizontally forced stratified turbulence: connecting exact coherent structures to linear instabilities. J. Fluid Mech. 832, 409–437.Google Scholar
Lucas, D., Caulfield, C. & Kerswell, R. 2019 Layer formation and relaminarisation in plane Couette flow with spanwise stratification. J. Fluid Mech. 868, 97–118.Google Scholar
Lucas, D. & Kerswell, R. R. 2015 Recurrent flow analysis in spatiotemporally chaotic 2-dimensional Kolmogorov flow. Phys. Fluids 27 (4), 045106.Google Scholar
Mellibovsky, F., Meseguer, A., Schneider, T. M. & Eckhardt, B. 2009 Transition in localized pipe flow turbulence. Phys. Rev. Lett. 103 (5), 054502.Google Scholar
Munk, W. H. 1966 Abyssal recipes. Deep-Sea Res. 13 (4), 707–730.Google Scholar
Oglethorpe, R. L. F., Caulfield, C. P. & Woods, A. W. 2013 Spontaneous layering in stratified turbulent Taylor–Couette flow. J. Fluid Mech. 721, R3.Google Scholar
Olvera, D. & Kerswell, R. R. 2017 Exact coherent structures in stably stratified plane Couette flow. J. Fluid Mech. 826, 583–614.Google Scholar
Papavassiliou, D. V. & Hanratty, T. J. 1997 Transport of a passive scalar in a turbulent channel flow. Intl J. Heat Mass Transfer 40 (6), 1303–1311.Google Scholar
Park, Y.-G., Whitehead, J. A. & Gnanadeskian, A. 1994 Turbulent mixing in stratified fluids: layer formation and energetics. J. Fluid Mech. 279, 279–311.Google Scholar
Prat, V., Guilet, J., Viallet, M. & Müller, E. 2016 Shear mixing in stellar radiative zones. II. Robustness of numerical simulations. Astron. Astrophys. 592, A59.Google Scholar
Prat, V. & Lignières, F. 2013 Turbulent transport in radiative zones of stars. Astron. Astrophys. 551, L3.Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.Google Scholar
Ruddick, B. R., McDougall, T. J. & Turner, J. S. 1989 The formation of layers in a uniformly stirred density gradient. Deep-Sea Res. 36 (4), 597–609.Google Scholar
Schlichting, H. & Gersten, K. 2016 Boundary-Layer Theory. Springer.Google Scholar
Schneider, T. M., Eckhardt, B. & Yorke, J. A. 2007 Turbulence transition and the edge of chaos in pipe flow. Phys. Rev. Lett. 99 (3), 034502.Google Scholar
Schneider, T. M., Marinc, D. & Eckhardt, B. 2010 Localized edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
Smith, F. T. & Bodonyi, R. J. 1982 Amplitude-dependent neutral modes in the Hagen–Poiseuille flow through a circular pipe. Proc. R. Soc. Lond. A 384 (1787), 463–489.Google Scholar
Suri, B., Tithof, J., Grigoriev, R. O. & Schatz, M. F. 2017 Forecasting fluid flows using the geometry of turbulence. Phys. Rev. Lett. 118 (11), 114501.Google Scholar
Suri, B., Tithof, J., Grigoriev, R. O. & Schatz, M. F. 2018 Unstable equilibria and invariant manifolds in quasi-two-dimensional Kolmogorov-like flow. Phys. Rev. E 98 (2), 023105.Google Scholar
Sutherland, B. R., Achatz, U., Caulfield, C. P. & Klymak, J. M. 2019 Recent progress in modeling imbalance in the atmosphere and the ocean. Phys. Rev. Fluids 4, 010501.Google Scholar
Thorpe, S. A. 2016 Layers and internal waves in uniformly stratified fluids stirred by vertical grids. J. Fluid Mech. 793, 380–413.Google Scholar
Tuckerman, L. S. 1989 Steady-state solving via Stokes preconditioning; recursion relations for elliptic operators. In 11th International Conference on Numerical Methods in Fluid Dynamics, p. 577. Springer.Google Scholar
Tuckerman, L. S., Langham, J. & Willis, A. 2019 Order-of-magnitude speedup for steady states and traveling waves via Stokes preconditioning in Channelflow and Openpipeflow. In Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics, pp. 3–31. Springer.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Viswanath, D. & Cvitanović, P. 2009 Stable manifolds and the transition to turbulence in pipe flow. J. Fluid Mech. 627, 215–233.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Willis, A. P., Cvitanović, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.Google Scholar
Zahn, J.-P. 1992 Circulation and turbulence in rotating stars. Astron. Astrophys. 265, 115–132.Google Scholar
Zhou, Q., Taylor, J. R. & Caulfield, C. P. 2017a Self-similar mixing in stratified plane Couette flow for varying Prandtl number. J. Fluid Mech. 820, 86–120.Google Scholar
Zhou, Q., Taylor, J. R., Caulfield, C. P. & Linden, P. F. 2017b Diapycnal mixing in layered stratified plane Couette flow quantified in a tracer-based coordinate. J. Fluid Mech. 823, 198–229.Google Scholar