Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T04:15:29.460Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex cusps

Published online by Cambridge University Press:  11 November 2019

Volker W. Elling Open the ORCID record for Volker W. Elling [Opens in a new window]
Volker W. Elling*
Affiliation:
Department of Mathematics, Academia Sinica, Taipei 10617, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

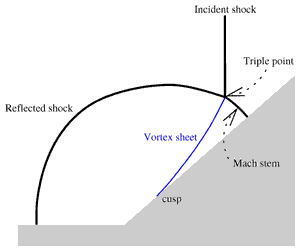
We consider pairs of self-similar two-dimensional vortex sheets forming cusps, equivalently single sheets merging into slip condition walls, as in classical Mach reflection at wedges. We derive from the Birkhoff–Rott equation a reduced model yielding formulas for cusp exponents and other quantities as functions of the similarity exponent and strain coefficient. Comparison to numerics shows that the piecewise quadratic and higher approximation of vortex sheets agree with each other and with the model. In contrast, piecewise linear schemes produce spurious results and violate conservation of mass, a problem that may have been undetected in prior work for other vortical flows. We find that vortex cusps only exist if the similarity exponent is sufficiently large and if the circulation on the sheet is counterclockwise (for a sheet above the wall with cusp opening to the right), unless a sufficiently positive strain coefficient compensates. Whenever a cusp cannot exist a spiral-ended jet forms instead; we find many jets are so narrow that they appear as false cusps.

JFM classification

Vortex Flows: Contour dynamics Interfacial Flows (free surface): Contact lines Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A17
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, R. C. 1971 Family of similarity flows with vortex sheets. Phys. Fluids 14 (2), 231–239.Google Scholar
Ben-Dor, G. 1992 Shock Wave Reflection Phenomena. Springer.Google Scholar
Birkhoff, G. 1962 Helmholtz and Taylor instability. Proc. Sympos. Appl. Math. 13, 55–76.Google Scholar
Elling, V. 2016 Self-similar 2d Euler solutions with mixed-sign vorticity. Commun. Math. Phys. 348 (1), 27–68.Google Scholar
Elling, V.2019a Triple shocks and sign of circulation. Phys. Fluids (submitted).Google Scholar
Elling, V.2019b Vortex cusps. arXiv:1901.09915.Google Scholar
Elling, V. & Gnann, M. V. 2019 Variety of unsymmetric multibranched logarithmic vortex spirals. Eur. J. Appl. Maths 30 (1), 23–38.Google Scholar
Henderson, L. F. & Menikoff, R. 1998 Triple-shock entropy theorem and its consequences. J. Fluid Mech. 366, 179–210.Google Scholar
Henderson, L. F., Vasilev, E. I., Ben-Dor, G. & Elperin, T. 2003 The wall-jetting effect in Mach reflection: theoretical consideration and numerical investigation. J. Fluid Mech. 479, 259–286.Google Scholar
Hornung, H. 1986 Regular and Mach reflection of shock waves. Annu. Rev. Fluid Mech. 18, 33–58.Google Scholar
Kaden, H. 1931 Aufwicklung einer unstabilen Unstetigkeitsfläche. Ing.-Arch. 2, 140–168.Google Scholar
Kaneda, Y. 1989 A family of analytical solutions of the motions of double-branched spiral vortex sheets. Phys. Fluids A 1, 261–266.Google Scholar
Krasny, R. 1991 Computing vortex sheet motion. In Proceedings of the International Congress of Mathematicians, vol. I, II, pp. 1573–1583. Springer.Google Scholar
Lopes-Filho, M. C., Lopes, H. J. N. & Schochet, S. 2007 A criterion for the equivalence of the Birkhoff-Rott and Euler descriptions of vortex sheet evolution. Trans. Am. Math. Soc. 359 (9), 4125–4142.Google Scholar
Mach, E. & Wosyka, J. 1875 Über die Fortpflanzungsgeschwindigkeit von Explosionsschallwellen. Sitzungsber. Akad. Wiss. Wien (II. Abth.) 72, 44–52.Google Scholar
Mangler, K. W. & Weber, J. 1967 The flow field near the center of a rolled-up vortex sheet. J. Fluid Mech. 30, 177–196.Google Scholar
Meiron, D., Baker, G. & Orszag, S. 1982 Analytic structure of vortex sheet dynamics. Part I. Kelvin–Helmholtz instability. J. Fluid Mech. 114, 283–298.Google Scholar
Moore, D. W. 1975 The rolling-up of a semi-infinite vortex sheet. Proc. R. Soc. Lond. A 345, 417–430.Google Scholar
von Neumann, J.1943 Oblique reflection of shocks. In Collected Works, vol. 6, pp. 238–299. (Tech. Rep. 12. Navy Dep., Bureau of Ordnance).Google Scholar
Nitsche, M. 2001 Self-similar shedding of vortex rings. J. Fluid Mech. 435, 397–407.Google Scholar
Prandtl, L. 1924 Über die Entstehung von Wirbeln in der idealen Flüssigkeit, mit Anwendung auf die Tragflügeltheorie und andere Aufgaben. In Vorträge aus dem Gebiet der Hydro- und Aerodynamik. Springer.Google Scholar
Pullin, D. 1978 The large-scale structure of unsteady self-similar rolled-up vortex sheets. J. Fluid Mech. 88 (3), 401–430.Google Scholar
Pullin, D. 1989 On similarity flows containing two-branched vortex sheets. In Mathematical Aspect of Vortex Dynamics (ed. Caflisch, R.), pp. 97–106. SIAM.Google Scholar
Rott, N. 1956 Diffraction of a weak shock with vortex generation. J. Fluid Mech. 1, 111–128.Google Scholar
Serre, D. 2007 Shock reflection in gas dynamics. In Handbook of Mathematical Fluid Mechanics, vol. 4, pp. 39–122.Google Scholar
Stern, M. 1956 The rolling-up of a vortex sheet. Z. Angew. Math. Phys. 7, 326–342.Google Scholar
Van Dyke, M. 1982 An Album of Fluid Motion. The Parabolic Press.Google Scholar
Vasilev, E. I., Ben-Dor, G., Elperin, T. & Henderson, L. F. 2004 The wall-jetting effect in Mach reflection: Navier–Stokes simulations. J. Fluid Mech. 511, 363–379.Google Scholar