1 Introduction
Mode decomposition methods have been used to understand the physics of complicated fluid flow phenomena containing high nonlinearity and a chaotic nature. Proper orthogonal decomposition (POD) (Lumley Reference Lumley, Yaglom and Tatarski1967) and dynamic mode decomposition (DMD) (Schmid Reference Schmid2010) are well-known methods for reduced-order modelling, which efficiently extract low-dimensional modes. With both methods, the key structures embedded in the time series of flow fields can be found and visualized, although there is a difference in the sense that POD determines the optimal set of modes to represent data based on the energy norm, while DMD captures dynamic modes with associated growth rates and frequencies (Taira et al.
Reference Taira, Brunton, Dawson, Rowley, Colonius, McKeon, Schmidt, Gordeyev, Theofilis and Ukeiley2017). These methods have helped us to understand the important structures underlying flow phenomena and to compare flow fields under different conditions (Murray, Sallstrom & Ukeiley Reference Murray, Sallstrom and Ukeiley2009). In addition, it is possible to construct control laws based on reduced-order models at low computational cost (Bergmann, Cordier & Brancher Reference Bergmann, Cordier and Brancher2005; Samimy et al.
Reference Samimy, Debiasi, Caraballo, Serrani, Yuan, Little and Myatt2007; Rowley & Dawson Reference Rowley and Dawson2017), since the time-evolving flow field can be represented by a linear combination of the expansion coefficients and the orthogonal bases. However, it is not easy to deal with highly nonlinear problems, such as high Reynolds number flows, using the conventional reduced-order models because of their linear nature. With POD, for example, 7260 modes are necessary to reproduce 95 % of the total energy for a turbulent channel flow at
$Re_{\unicode[STIX]{x1D70F}}=180$
(Alfonsi & Primavera Reference Alfonsi and Primavera2007), while we need only two POD modes to reproduce 99 % of total energy for a flow around a circular cylinder at
$Re_{D}=100$
. This limitation narrows the applicability of the conventional reduced-order models to various flow fields.
In recent years, machine learning has been widely applied in the field of fluid dynamics, and is highly regarded for its strong ability to account for nonlinearity (Brunton & Noack Reference Brunton and Noack2015; Kutz Reference Kutz2017; Taira et al. Reference Taira, Hemati, Brunton, Sun, Duraisamy, Bagheri, Dawson and Yeh2019; Brunton, Noack & Koumoutsakos Reference Brunton, Noack and Koumoutsakos2020). Ling, Kurzawski & Templeton (Reference Ling, Kurzawski and Templeton2016) used a customized multi-layer perceptron accounting for the Galilean invariance for Reynolds-averaged Navier–Stokes turbulence modelling. For large-eddy simulation, Maulik & San (Reference Maulik and San2017) used a multi-layer perceptron to estimate the eddy viscosity with the blind deconvolution method. The recent efforts in turbulence modelling are summarized well in Duraisamy, Iaccarino & Xiao (Reference Duraisamy, Iaccarino and Xiao2019). Machine learning has been also utilized for reduced-order modelling. San & Maulik (Reference San and Maulik2018) proposed an extreme learning machine based reduced-order modelling for turbulent systems and showed its advantage against POD. The multi-layer perceptron and long short term memory are utilized to develop temporally evolved turbulence with a nine-equation shear flow model by Srinivasan et al. (Reference Srinivasan, Guastoni, Azizpour, Schlatter and Vinuesa2019). In this way, the fusion of machine learning and fluid dynamics is ongoing now.
In particular, the convolutional neural network (CNN) (LeCun et al. Reference LeCun, Bottou, Bengio and Haffner1998), widely used for image processing, has been utilized as an appropriate method to deal with flow field data with the advantage that we can handle fluid big data with reasonable computational cost thanks to the concept of filters, called weight sharing. Fukami, Fukagata & Taira (Reference Fukami, Fukagata and Taira2019a ) performed a super-resolution analysis for two-dimensional turbulence using a customized CNN to account for multi-scale phenomena. The deep CNNs were also considered to predict small scale ocean turbulence, called ‘atoms’ by Salehipour & Peltier (Reference Salehipour and Peltier2019). Of particular interest for CNN is the application for dimension reduction via an autoencoder (Hinton & Salakhutdinov Reference Hinton and Salakhutdinov2006). An autoencoder composed of linear perceptrons is known to work similarly to POD (Baldi & Hornik Reference Baldi and Hornik1989). For applications to fluid mechanics, Milano & Koumoutsakos (Reference Milano and Koumoutsakos2002) have successfully demonstrated, through various problems such as the randomly forced Burgers equation and turbulent channel flows, that the capability of an autoencoder is significantly improved by adopting nonlinear multi-layer perceptrons. In addition, autoencoders have recently exhibited their remarkable ability in combination with CNN not only in the field of image processing but also in fluid mechanics. Omata & Shirayama (Reference Omata and Shirayama2019) proposed a method utilizing a CNN autoencoder with POD to reduce the dimension of two-dimensional airfoil flow data. These concepts have also been applied to develop an inflow turbulence generator by Fukami et al. (Reference Fukami, Nabae, Kawai and Fukagata2019b ). Despite these favourable properties, the conventional CNN autoencoders are interpretable only in terms of the input, the latent vector (i.e. the intermediate low-dimensionalized data) and the output – the flow fields cannot be decomposed nor visualized like POD or DMD, which can extract the individual representation of low-dimensional mapping.
In this study, we present a new flow decomposition method based on a CNN autoencoder which can take account nonlinearity into its structure in order to decompose flow fields into nonlinear low-dimensional modes and to visualize each mode. We apply this method to a flow around a circular cylinder at
$Re_{D}=100$
to clarify what the network actually learns about the flow.
2 Methods
2.1 Training data
The training data are obtained by a two-dimensional direct numerical simulation (DNS) of flow around a circular cylinder. The governing equations are the incompressible continuity and Navier–Stokes equations,
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}}=-\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{u}\boldsymbol{u})-\unicode[STIX]{x1D735}p+{\displaystyle \frac{1}{Re_{D}}}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}, & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{u}$
and
$p$
denote the velocity vector and pressure, respectively. All quantities are made dimensionless by the fluid density, the free-stream velocity and the cylinder diameter. The Reynolds number based on the cylinder diameter is
$Re_{D}=100$
. The size of the computational domain is
$L_{x}=25.6$
and
$L_{y}=20.0$
in the streamwise (
$x$
) and the transverse (
$y$
) directions, respectively. The origin of coordinates is defined at the centre of the inflow boundary, and the cylinder centre is located at
$(x,y)=(9,0)$
. A Cartesian grid system with a grid spacing of
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=0.025$
is used. The number of grid points is
$(N_{x},N_{y})=(1024,800)$
. The no-slip boundary condition on the cylinder surface is imposed using the ghost cell method of Kor, Badri Ghomizad & Fukagata (Reference Kor, Badri Ghomizad and Fukagata2017).
In the present study, we focus on the flows around the cylinder. For the first case with periodic vortex shedding under a statistically steady state, we extract a part of the computational domain, i.e.
$8.2\leqslant x\leqslant 17.8$
and
$-2.4\leqslant y\leqslant 2.4$
. Thus, the number of the grid points used for machine learning is
$(N_{x}^{\ast },N_{y}^{\ast })=(384,192)$
. As the input and output attributes, the fluctuation components of streamwise velocity
$u$
and transverse velocity
$v$
are utilized. The time interval of the flow field data is 0.25 corresponding to approximately 23 snapshots per a cycle with the Strouhal number equals to 0.172. For the second case with a transient wake, the computational procedure is the same, but a larger domain is used, as explained later in § 3.2.
2.2 Machine learning model
Figure 1. Internal operations of convolutional neural network: (a) convolutional layer, (b) pooling layer and (c) upsampling layer.
A convolutional neural network (CNN) mainly consists of three layers: the convolutional layer, pooling layer and upsampling layer. The main procedure in the convolutional layer is illustrated in figure 1(a). Using a filter with a size of
$H\times H\times K$
on the input
$z_{ijk}^{(l-1)}$
for a pixel represented by indices
$(i,j,k)$
, the filtered data
$c_{ijm}$
on a pixel
$(i,j,m)$
are given by
$$\begin{eqnarray}\displaystyle & \displaystyle c_{ijm}^{(l)}=\mathop{\sum }_{k=0}^{K-1}\mathop{\sum }_{s=0}^{H-1}\mathop{\sum }_{t=0}^{H-1}z_{i+s,j+t,k}^{(l-1)}w_{stkm}^{(l)}+b_{ijm}^{(l)}, & \displaystyle\end{eqnarray}$$
where
$w_{stkm}^{(l)}$
and
$b_{ijm}^{(l)}$
denote the weight and the bias at layer
$l$
, respectively. In the present paper, the input and output of the autoencoder model are represented as
$z^{(0)}=z^{(l_{max})}=\boldsymbol{q}=\{u,v\}$
. For this value, the activation function
$\unicode[STIX]{x1D713}$
is applied to obtain the output of this layer,
$$\begin{eqnarray}\displaystyle z_{ijm}^{(l)}=\unicode[STIX]{x1D713}(c_{ijm}^{(l)}). & & \displaystyle\end{eqnarray}$$
In general, a nonlinear function is used as the activation function of hidden layers, as explained later. With the pooling layer shown in figure 1(b), the data are compressed by
$(1/P)^{2}$
times in such a way that the maximum value represents a region with a size of
$P\times P$
, i.e. max pooling. By combining the convolutional and pooling layers, it is possible to reduce the dimensions while retaining the features of the input data. In the process of enlarging the data dimension, the upsampling layer is used to expand the data by copying, as shown in figure 1(c).
Figure 2. Schematic of two types of CNN autoencoder used in the present study; (a) conventional type CNN autoencoder (C-CNN-AE), and (b) mode decomposing CNN autoencoder (MD-CNN-AE).
The concept of the conventional type CNN autoencoder (C-CNN-AE) is illustrated in figure 2(a). It consists of two parts: an encoder
${\mathcal{F}}_{enc}$
and a decoder
${\mathcal{F}}_{dec}$
. The encoder works to map the high-dimensional flow field into a low-dimensional space. In the present study, we map the flow around a cylinder into a two-dimensional latent space (shown as
$r_{1}$
and
$r_{2}$
in figure 2). The decoder is used to expand the dimension from the latent space. In the encoder
${\mathcal{F}}_{enc}$
, the input data
$\boldsymbol{q}$
with the size of
$(N_{x}^{\ast },N_{y}^{\ast },N_{\unicode[STIX]{x1D719}})=(384,192,2)$
, where
$N_{\unicode[STIX]{x1D719}}$
is the size of the feature vector, are mapped to the latent vector
$\boldsymbol{r}$
with the size of
$(2,1,1)$
, i.e. two values. In the decoder
${\mathcal{F}}_{dec}$
, the output data
$\tilde{\boldsymbol{q}}$
having the same dimension as
$\boldsymbol{q}$
are restored from the latent vector
$\boldsymbol{r}$
. We summarize this in the formula,
$$\begin{eqnarray}\displaystyle \boldsymbol{r}={\mathcal{F}}_{enc}(\boldsymbol{q}),\quad \tilde{\boldsymbol{q}}={\mathcal{F}}_{dec}(\boldsymbol{r}). & & \displaystyle\end{eqnarray}$$
The objective of the autoencoder is to seek the optimized weights
$\boldsymbol{w}$
so as to minimize the
$L_{2}$
error norm between the input and the output:
$\boldsymbol{w}=\text{argmin}_{\boldsymbol{w}}\Vert \tilde{\boldsymbol{q}}-\boldsymbol{q}\Vert _{2}^{2}.$
If the original data
$\boldsymbol{q}$
are successfully restored from
$\boldsymbol{r}$
, this suggests that the data are well represented in the dimensions of
$\boldsymbol{r}$
.
In the C-CNN-AE, the dimension reduction of the data can be done, but the intermediate output data are hard to interpret because the weights are randomly optimized during the process of training. Thus, we propose a mode decomposing CNN autoencoder (MD-CNN-AE) shown in figure 2(b). The encoder part of MD-CNN-AE is similar to that of C-CNN-AE, but the latent vector
$\boldsymbol{r}$
is divided into two variables,
$r_{1}=r_{1,1,1}$
and
$r_{2}=r_{2,1,1}$
, where the subscripts denote the indices of
$\boldsymbol{r}$
. The first decoder
${\mathcal{F}}_{dec1}$
is used to make the first decomposed field
$\tilde{\boldsymbol{q}_{1}}$
from the first variable
$r_{1}$
and the same for the second decoder
${\mathcal{F}}_{dec2}$
, i.e.
$\tilde{\boldsymbol{q}_{2}}$
from
$r_{2}$
. The summation of the two decomposed fields,
$\tilde{\boldsymbol{q}_{1}}$
and
$\tilde{\boldsymbol{q}_{2}}$
, is the output
$\tilde{\boldsymbol{q}}$
of MD-CNN-AE. In summary, the processes are
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{r}={\mathcal{F}}_{enc}(\boldsymbol{q}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\boldsymbol{q}_{1}}={\mathcal{F}}_{dec1}(r_{1}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\boldsymbol{q}_{2}}={\mathcal{F}}_{dec2}(r_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \tilde{\boldsymbol{q}}=\tilde{\boldsymbol{q}_{1}}+\tilde{\boldsymbol{q}_{2}}. & \displaystyle\end{eqnarray}$$
Since MD-CNN-AE has the same structure as POD in the sense that it obtains the fields for each low-dimensional mode and adds them, it can decompose flow fields in such a way that each mode can be visualized, which cannot be done with C-CNN-AE.
For the network parameters mentioned above, we choose the filter length
$H=3$
and
$K=2$
corresponding to
$\boldsymbol{q}=\{u,v\}$
, the max pooling ratio
$P=2$
and the number of the layers
$l_{max}=28$
. The details of the proposed machine learning models are summarized in table 1. The number of trainable parameters for the present MD-CNN-AE is 9646. For training both CNNs, we apply the early stopping criterion (Prechelt Reference Prechelt1998) to avoid overfitting and use the Adam algorithm (Kingma & Ba Reference Kingma and Ba2014) to seek the optimized weights
$\boldsymbol{w}$
. In the training process, 7000 randomly chosen snapshots of data are used as training data and 3000 snapshots were used as validation data. Fivefold cross-validation (Brunton & Kutz Reference Brunton and Kutz2019) is performed to make all machine learning models in the present study, although only the results of a single case will be shown for brevity. The other hyper parameters used in the present study are summarized in table 2. For further details on the implementation of MD-CNN-AE, interested readers are referred to the sample Python code available on our project webpage (http://kflab.jp/en/index.php?18H03758).
Figure 3. Activation functions used in the present study and
$L_{2}$
norm error for each method.
Table 1. The network structure of MD-CNN-AE constructed by an encoder and two decoders. The convolution layers and the max pooling layers are denoted as conv. and MaxPooling, respectively. Decoder 2 has the same structure as decoder 1.
Table 2. Hyper parameters used for the present MD-CNN-AE.
3 Results and discussion
3.1 Periodic vortex shedding case
First, we examine the MD-CNN-AEs with different activation functions: linear activation, rectified linear unit (ReLU), hyperbolic tangent function (tanh), standard sigmoid function (Sigmoid) and softsign function (Softsign), as summarized in figure 3. In this figure, we also present the
$L_{2}$
norm errors calculated by 2000 test snapshots in these five MD-CNN-AEs, excluding the training process, and compare them with the cases of C-CNN-AE with tanh activation (C-CNN-tanh) and POD with the first two modes only. In the case of Sigmoid, the network is not trained well because of the vanishing gradient problem. The CNN with linear activation has the same error level as POD, which suggests that the linear CNN is also similar to POD as in the case of fully connected multi-layer perceptrons with linear activation (Baldi & Hornik Reference Baldi and Hornik1989; Milano & Koumoutsakos Reference Milano and Koumoutsakos2002). When the nonlinear activation function (ReLU, tanh or Softsign) is used, the errors are less than that of linear activation and POD. Among them, tanh and Softsign, which have higher nonlinearity, result in lower
$L_{2}$
norm errors. From these results, it is confirmed that the nonlinearity is the key to improving the performance of the model. Comparing the network structures under the same activation function (i.e. tanh), MD-CNN-tanh has a slightly larger error than C-CNN-tanh because of its complex structure. In the following, we compare the results obtained by MD-CNN-AE with linear activation (MD-CNN-Linear) and that with tanh (MD-CNN-tanh) to investigate the effect of nonlinearity. Note that similar trends are observed in the other iterations for cross-validation.
Figure 4. The reference instantaneous flow field, output flow field and distribution of
$L_{2}$
norm error in the three methods: (a) streamwise velocity
$u$
, (b) transverse velocity
$v$
.
The output of the machine-learned models (MD-CNN-Linear and MD-CNN-tanh) and POD are summarized in figure 4. The flow fields reconstructed by all three methods show reasonable agreement with the reference data. The field reconstructed by MD-CNN-tanh is closest to the reference. Interestingly, the reconstructed fields of MD-CNN-Linear and POD are similar, which confirms the similarity mentioned above.
In order to evaluate the reconstruction error, we assess the time-averaged local
$L_{2}$
norm error with 2000 test snapshots excluding the training process, as shown in figure 4. Comparing the three methods, MD-CNN-tanh shows the lowest error in the entire region except for the very small region downstream of the cylinder. The distributions of
$L_{2}$
norm error in POD and MD-CNN-Linear are again similar due to their similarity mentioned above.
Figure 5. The decomposed flow fields with POD, MD-CNN-Linear and MD-CNN-tanh.
Figure 6. Encoded variables (
$r_{1},r_{2}$
) with MD-CNN-tanh: (a) time traces, (b) trajectory compared with that of POD.
The strength of the present MD-CNN-AE over the conventional CNN is that the flow field can be decomposed and visualized. Figure 5 visualizes the two decomposed fields corresponding to the velocity distributions of figure 4. Note that the time-averaged component of the decomposed fields is subtracted in MD-CNN-AEs. The decomposed field of POD and that of MD-CNN-Linear are almost the same, and the decomposed field of MD-CNN-tanh is distorted, likely due to the nonlinearity of the activation function. Figure 6 shows the time traces of the corresponding encoded variables (
$r_{1},r_{2}$
) by MD-CNN-tanh and compares the trajectory with that of POD. The encoded variables obtained by MD-CNN-tanh are also periodic in time, corresponding to the vortex shedding, but the phases are observed to be shifted from those of POD. It is worth noting that, although not shown here, the periodic signals of
$r_{1}$
and
$r_{2}$
are observed to be similar in the fivefold cross-validation but the amount of phase shift (i.e. trajectory) is not unique. This suggests that the decomposition by MD-CNN-tanh is not unique due to the nonlinearity.
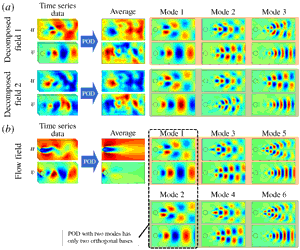
Figure 7. The POD orthogonal basis of two decomposed fields of MD-CNN-tanh and reference DNS.
To examine the distortion observed above further, we perform POD for the decomposed fields obtained by the MD-CNN-tanh model, as shown in figure 7(a). We also present in figure 7(b) the POD results of the reference flow field to compare with the machine-learned model. The interesting view is that decomposed field 1 contains the orthogonal bases akin to POD modes 1, 3 and 5, and decomposed field 2 contains modes 2, 4 and 6. Note that complicated structures observed in the average fields shown in figure 7(a) are mostly cancelled out by adding these decomposed fields. This suggests that the proposed method also decomposes the average field of the fluctuation components, which should be zero via the nonlinear function. It is also worth noting that the ratio of the amounts of kinetic energy contained in decomposed field 1 and decomposed field 2 are nearly equal.
Figure 8. Normalized value of the energy distribution of the orthogonal basis of the (a) flow field, (b) reconstructed field using POD with two modes only or MD-CNN-Linear and (c) reconstructed field using MD-CNN-tanh.
Let us present in figure 8 the normalized values of the energy distribution of the orthogonal bases contained in the flow field. When we use only the first two POD modes to reconstruct the flow field – as a matter of course due to the orthogonality of POD bases – decomposed field 1 consists of mode 1, and decomposed field 2 consists of mode 2, while higher modes are discarded, as indicated by the grey area of figure 8(b). The situation is the same for MD-CNN-Linear. On the other hand, for MD-CNN-tanh, the two decomposed fields contain multiple POD modes, and the characteristics of higher modes are retained, which results in the lower reconstruction error than for the POD with first two modes only. In addition, the flow field is decomposed in such a way that the orthogonal bases are distributed to two decomposed fields in a similar manner as the full POD, as shown in figure 8(c).
In the present example problem of two-dimensional flow around a cylinder, it is known that the third to sixth POD modes can be expressed by analytical nonlinear functions of the first two POD modes (Loiseau, Brunton & Noack Reference Loiseau, Brunton, Noack and Benner2020). The present result with MD-CNN-tanh is consistent with this knowledge, and it suggests that such nonlinear functions are embedded in the nonlinearity of MD-CNN-tanh.
Figure 9. Demonstration of the robustness analysis for noisy inputs with MD-CNN-tanh. (a) Streamwise velocity fluctuation
$u^{\prime }$
with
$\unicode[STIX]{x1D705}=0$
(without noise),
$0.1$
and
$1$
; (b)
$\unicode[STIX]{x1D705}-(\overline{\unicode[STIX]{x1D716}^{\prime }}/\overline{\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D705}=0}^{\prime }})$
plot. A fivefold cross-validation is undertaken although not shown here.
We also examine the robustness of the MD-CNN-tanh for a noisy input in order to assess the applicability for experimental situations, as shown in figure 9. Here, let the
$L_{2}$
norm error for a noisy input be
$\unicode[STIX]{x1D716}^{\prime }=||\boldsymbol{q}_{DNS}^{\prime }-{\mathcal{F}}(\boldsymbol{q}_{DNS}^{\prime }+\unicode[STIX]{x1D705}\boldsymbol{n})||_{2}^{2}$
, where
$\boldsymbol{q}$
is the feature vector,
$\boldsymbol{n}$
is Gaussian random noise with unit variance and
$\unicode[STIX]{x1D705}$
is the magnitude of noisy inputs. With
$\unicode[STIX]{x1D705}=0.1$
, the output of MD-CNN-tanh shows reasonable agreement with the input DNS data. Over
$\unicode[STIX]{x1D705}=0.1$
, the error drastically increases with an increasing magnitude of noise
$\unicode[STIX]{x1D705}$
, as shown in figure 9(b). Noteworthy here is that the MD-CNN-tanh has a denoising effect, as observed for
$\unicode[STIX]{x1D705}=0.1$
and
$1$
of figure 9(a). A similar observation has been reported by Erichson et al. (Reference Erichson, Mathelin, Yao, Brunton, Mahoney and Kutz2019), who applied multi-layer perceptrons to a cylinder wake.
Figure 10. (a) The lift coefficient
$C_{L}$
of the transient process; (b) normalized value of the energy distribution of first ten POD modes; (c) the corresponding vorticity fields.
3.2 Transient wake case
As an example of more complex flows comprising high-order modes, let us consider a transient process with a circular cylinder wake at
$Re_{D}=100$
. For the transient flow, the streamwise length of the computational domain and that of flow field data are extended to
$L_{x}=51.2$
and
$8.2\leqslant x\leqslant 37$
, i.e.
$N_{x}^{\ast }=1152$
. To focus on the transient process, we use the flow field data of
$50\leqslant t\leqslant 150$
with a time step of
$\unicode[STIX]{x0394}t=0.025$
. The temporal development of the lift coefficient
$C_{L}$
and the energy and vorticity fields of the first ten POD modes are summarized in figure 10. All of these quantities exhibit trends similar to those of Noack et al. (Reference Noack, Stankiewicz, Morzynski and Schmid2016).
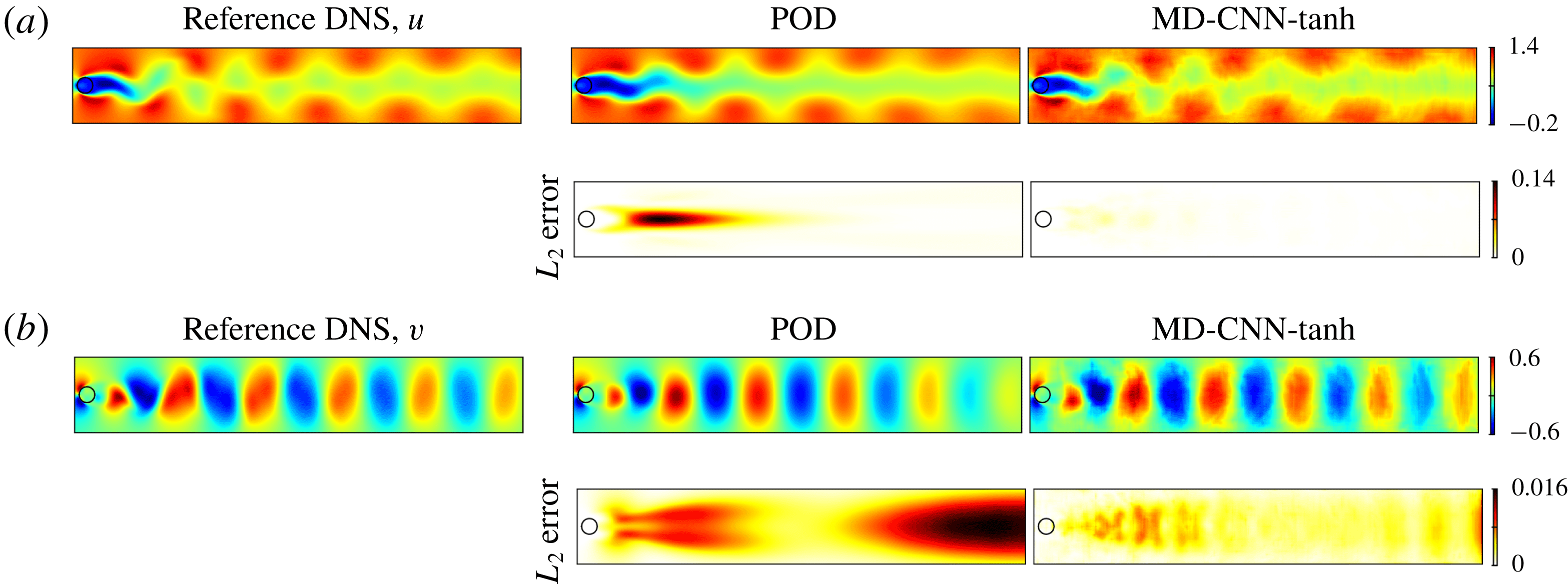
Figure 11. The reference instantaneous flow field, output flow field and distribution of
$L_{2}$
norm error at
$t=137.5$
with two methods: (a) streamwise velocity
$u$
and (b) transverse velocity
$v$
.
Figure 11 compares the reference DNS flow fields and the fields reconstructed by POD and MD-CNN-tanh using the first two modes. Similarly to the results shown in figure 4, the proposed method shows lower
$L_{2}$
error than POD.
Figure 12. The POD orthogonal basis of (a) two decomposed fields of MD-CNN-tanh and (b) reference DNS in a transient flow.
Figure 13. The energy distribution of the DNS and output field with MD-CNN-tanh.
In figure 12, we summarize the results of performing POD to the decomposed field 1 and field 2 obtained by MD-CNN-tanh, compared with the POD modes obtained from DNS data, as in figure 7. Here, the average fields of time series data are omitted and the decomposed field 2 is shown on the top for clarity of illustration. The energy distribution of the output field of MD-CNN-tanh with two latent vectors, obtained by POD, is shown in figure 13. Similarly to figure 7(b), one decomposed field (field 2 in this figure) contains the orthogonal bases, like POD modes 1, 3 and 5, and another decomposed field contains POD modes 2, 4 and 7. The difference from figure 7(b) is that a mode resembling POD mode 7 appears in this case instead of mode 6. This model likely estimates that mode 7 has higher energy than mode 6, since POD mode 7 has the same degree of energy as mode 6, as shown in figure 13. In summary, in this transient case also, a single nonlinear mode of MD-CNN-tanh contains multiple POD modes in a manner broadly similar to the periodic vortex shedding case, although the correspondence to the POD modes is slightly less clear.
Figure 14. Dependence on the number of latent vector (i.e. mode used for reconstruction) for the transient wake problem. A fivefold cross-validation is undertaken although the error bars are not shown here.
Finally, as a preliminary investigation toward extension of the present method, we show in figure 14 a result for the dependence on the number of latent vector
$n_{L}$
for the transient wake problem, although further investigation of the
$n_{L}>2$
cases is left as future work. Here, we compare POD and MD-CNN-AEs with
$n_{L}=2$
, 4 and 8. It is observed that the
$L_{2}$
error of MD-CNN-AE is systematically less than that of POD with the same number of modes. This result suggests that the present model can map the high-dimensional data into a lower-dimensional space than POD while retaining the feature of the unsteady flow. However, the present result also implies that the ability of MD-CNN-AE to represent the flow with fewer modes is not as good as the most advanced nonlinear dimensionality reduction methods, such as locally linear embedding (LLE) (Roweis & Lawrence Reference Roweis and Lawrence2000), by which Ehlert et al. (Reference Ehlert, Nayeri, Morzynski and Noack2019) has very recently reported that reconstruction using 2 LLE coordinates results in a much lower
$L_{2}$
error than that using 10 POD modes.
4 Conclusions
As a CNN structure which can decompose flow fields in a nonlinear manner and visualize the decomposed fields, we constructed a mode decomposing CNN autoencoder (MD-CNN-AE) with one encoder and two decoders. As a test case, the method was applied to flow around a circular cylinder at
$Re_{D}=100$
, and the flow field was mapped into two values and restored by adding the two decomposed fields. With MD-CNN-Linear, which has linear activation functions, the reconstructed field is similar to that of POD with the first two modes, both in terms of
$L_{2}$
norm error and the distribution of reconstruction error. This suggests that the linear CNN is also similar to POD as in the case of linear multi-layer perceptrons. When we use the nonlinear activation function, the
$L_{2}$
norm error of reconstruction was reduced as compared to those of POD with two modes and MD-CNN-Linear.
We also investigated the decomposed fields obtained by MD-CNN-AE. The two decomposed fields in MD-CNN-Linear are similar to those of POD with two modes. For MD-CNN-tanh, complex structures were observed and the two decomposed fields of MD-CNN-tanh were found to have the same amount of energy. By performing POD for these two decomposed fields, it was revealed that decomposed field 1 contains the orthogonal bases corresponding to POD modes 1, 3 and 5, and decomposed field 2 contains modes 2, 4 and 6. The present result is also consistent with the existing knowledge on the relationship between the first two POD modes and the third to sixth POD modes in the present problem – this suggests that MD-CNN-tanh can be used to extract modes with lower dimensions in such a way that nonlinear functions are embedded in the network. A transient process was also considered as an example of more complex flow with higher-order spatial modes, and broadly similar results were obtained.
Through the analysis of very simple problems, i.e. an unsteady cylinder wake and its transient process, we have confirmed the basic performance of the proposed MD-CNN-AE. However, the proposed method has been so far examined only for flows with large scale spatial structures. To handle more complex flows, e.g. turbulence, additional improvements on the network design are required. Nevertheless, we believe that by extending the present idea of MD-CNN-AE with a nonlinear function, which can represent more information against linear theory with same number of modes, we may be able to take greater advantage of machine learning for reduced-order modelling of three-dimensional unsteady and turbulent flows, that can eventually be utilized for development of efficient flow control laws based on nonlinear reduced-order models.
Acknowledgements
Authors are grateful to Drs S. Obi, K. Ando and Mr K. Hasegawa (Keio University) for fruitful discussions, and Dr K. Zhang (UCLA) for comments and advice for the analysis of transient flows. K. Fukagata also thanks Dr K. Taira (UCLA) for advising K. Fukami during his exchange. This work was supported through JSPS KAKENHI grant no. 18H03758 by Japan Society for the Promotion of Science.
