This article describes recent progress on premixed flame dynamics interacting with acoustic waves. Expressions are derived to determine the stability of combustors with respect to thermoacoustic oscillations. The validity of these expressions is general, but they are illustrated in laminar systems. Laminar burners are commonly used to elucidate the response of premixed flames to incoming flow perturbations, highlight the role of acoustic radiation in their stability, identify modes associated with thermoacoustic intrinsic instabilities and decipher the leading mechanisms in annular systems with multiple injectors. Many industrial devices also operate in a laminar premixed mode such as, for example, domestic gas boilers and heaters equipped with matrix burners for material processing in which unconfined flames are stabilized at one extremity of the system. This article proposes a systematic approach to determine the stability of all these systems with respect to thermoacoustic oscillations by highlighting the key role of the burner impedance and the flame transfer function (FTF). This transfer function links in frequency space incoming flow perturbations to heat release rate disturbances. This concept can be used in the turbulent flame case as well. Weakly nonlinear stability analysis can also easily be conducted by replacing the FTF by a flame describing function in the expressions derived in this work. The response of premixed flames to harmonic mixture compositions and flow-rate perturbations is then revisited and the main parameters controlling the FTF are described. A theoretical framework is finally developed to reduce the system thermoacoustic sensitivity by tailoring the FTF.

Coasts are obstructions to the classical derivation of continuously stratified quasi-geostrophic equations, due to possible resonances between slow internal coastally trapped Kelvin waves and anticyclones. Deremble et al. (Ocean Model., vol. 119, 2017, pp. 1–12) proposed a coupled model between a quasi-geostrophic interior and boundary-layer Kelvin-wave dynamics. We revisit the derivation of this model, paying particular attention to conservation laws. We find that quasi-geostrophic energy is conserved, despite the existence of Kelvin-wave shocks in the boundary layer. The effect of those shocks is to change the global distribution of potential vorticity, and, consequently, the interior flow structure. In that respect, we show that there is an active control of the boundary region on the interior flow.

Helicity, as one of only two inviscid invariants in three-dimensional turbulence, plays an important role in the generation and evolution of turbulent flows. Through theoretical analyses, we find that there are two channels in the helicity cascade process, which differs dramatically from the traditional viewpoint. In this paper, we have conducted important research on the newly proposed dual-channel helicity cascade theory, including vortex dynamic processes, intermittent discrepancies, tensor geometries, etc. The first channel mainly originates from the vortex twisting process, and the second channel mainly originates from the vortex stretching process. Antisymmetric tensors are introduced to the derivations of dual-channel helicity cascade theory, and a complex rotation frame leads to a higher helicity transfer efficiency. By analysing data from direct numerical simulations of typical turbulent flows, we find that these two channels behave differently. The ensemble averages of helicity flux in different channels are equal in homogeneous and isotropic turbulence, while they are different in other types of turbulent flows. The intermittency of the second channel is stronger than that of the first channel. In addition, we find a novel mechanism of hindered or even inverse energy cascades, which could be attributed to the second-channel helicity flux.

In nonlinear dynamics, there are three classic routes to chaos, namely the period-doubling route, the Ruelle–Takens–Newhouse route and the intermittency route. The first two routes have previously been observed in self-excited thermoacoustic systems, but the third has not. In this experimental study, we present evidence of the intermittency route to chaos in the self-excited regime of a prototypical thermoacoustic system – a laminar flame-driven Rijke tube. We identify the intermittency to be of type II from the Pomeau–Manneville scenario through an analysis of (i) the probability distribution of the quiescent epochs between successive bursts of chaos, (ii) the first return map, and (iii) the recurrence plot. By establishing the last of the three classic routes to chaos, this study strengthens the universality of how strange attractors arise in self-excited thermoacoustic systems, paving the way for the application of generic suppression strategies based on chaos control.

A wide class of problems for free-surface gravity waves fall into a weakly dispersive regime, in which wavelength is large compared to water depth, and wave phase speed differs by a small amount from the speed $c_{0}=\sqrt{gh}$ of shallow-water waves. The resulting problem is treated naturally using Taylor series expansions of dependent variables in the vertical coordinate, leading to a class of models that are collectively referred to here as Boussinesq-type models. Madsen & Fuhrman (J. Fluid Mech., vol. 889, 2020, A38) have recently shown that certain members of this broad class of models are subject to a high-wavenumber instability, which can grow rapidly when the elevation of the wave trough is sufficiently depressed below the mean water surface. This newly revealed instability may provide an explanation for the modelling community’s frequent observations of noisy behaviour in Boussinesq-type model calculations.

Flow physics plays a key role in nearly every facet of the COVID-19 pandemic. This includes the generation and aerosolization of virus-laden respiratory droplets from a host, its airborne dispersion and deposition on surfaces, as well as the subsequent inhalation of these bioaerosols by unsuspecting recipients. Fluid dynamics is also key to preventative measures such as the use of face masks, hand washing, ventilation of indoor environments and even social distancing. This article summarizes what we know and, more importantly, what we need to learn about the science underlying these issues so that we are better prepared to tackle the next outbreak of COVID-19 or a similar disease.

Kang et al. (J. Fluid Mech., vol. 874, 2019, pp. 339–358) studied viscous dissipation within a permeable body with a view to maximizing the damping of oscillations of the body. They found that dissipation is maximal when the length scale for diffusion of vorticity in the fluid outside the body is similar to the length scale for decay of fluid motion within the body. Their results are examined in the context of the simpler problem of a porous half-space oscillating parallel to the interface between porous solid and fluid. The analysis is then extended to consider the impulsive start-up from rest of a porous plane surface adjacent to unbounded fluid.

This paper presents a theory based on the law of momentum conservation to define and help analyse the problem of large wind farm aerodynamics. The theory splits the problem into two subproblems; namely an ‘external’ (or farm-scale) problem, which is a time-dependent problem considering large-scale motions of the atmospheric boundary layer (ABL) to assess the amount of momentum available to the bottom resistance of the ABL at a certain time; and an ‘internal’ (or turbine-scale) problem, which is a quasi-steady (in terms of large-scale motions of the ABL) problem describing the breakdown of the bottom resistance of the ABL into wind turbine drag and land/sea surface friction. The two subproblems are coupled to each other through a non-dimensional parameter called ‘farm wind-speed reduction factor’ or ‘farm induction factor,’ for which a simple analytic equation is derived that can be solved iteratively using information obtained from both subproblems. This general form of coupling allows us to use the present theory with various types of flow models for each scale, such as a numerical weather prediction model for the external problem and a computational fluid dynamics model for the internal problem. The theory is presented for a simplified wind farm situation first, followed by a discussion on how the theory can be applied (in an approximate manner) to real-world problems; for example, how to estimate the power loss due to the so-called ‘wind farm blockage effect’ for a given large wind farm under given environmental conditions.

Here we characterize the origin and subsequent disintegration into droplets of the type of high-speed jets formed after the sudden implosion of a locally spherical cavity. The full spatio-temporal evolution of these types of impulsively generated jets is described here making use of just the initial values of the interfacial normal velocity at the axis of symmetry and of its corresponding second derivative along the azimuthal direction, obtained straightforwardly from the solution of the Laplace equation subjected to standard boundary conditions. The predicted time evolutions of the jet tip radius and velocity, and of the radii of the ejected droplets, are shown to agree well with experimental observations.

The highly convoluted interface separating the turbulent and non-turbulent regions in a turbulent mixing layer is experimentally investigated using the particle image velocimetry (PIV) technique. The mixing layer was generated using a fine screen/mesh in one half of the test section of a low-speed wind tunnel. The PIV data, which were acquired with high spatial resolution in the self-similar regime of the flow, allow us to identify the turbulent/non-turbulent interface (TNTI) using a suitable threshold value of the absolute spanwise vorticity, $|\unicode[STIX]{x1D714}_{z}|$. The threshold values for the top and bottom interfaces of the mixing layer are found to be different, and the probability density function (PDF) of the interface position for both the interfaces is found to follow the Gaussian distribution. Interestingly, the PDF of the interface orientation reveals two clear peaks, and this is attributed to the sustained large-scale motions in a mixing layer, compared to the other free-shear flows, as is also substantiated by further analyses such as the linear stochastic estimation and the conditional analysis of the transverse velocity profile. The linear stochastic analysis also shows the presence of large vorticity structures of the order of the Taylor microscale at the mean TNTI location in a mixing layer. Furthermore, the present work reveals that, using the spanwise component of vorticity alone, we can experimentally identify and estimate the thickness of the viscous superlayer from the conditional profiles of the diffusion term and the correlation coefficient of the dissipation and the diffusion terms in the enstropy transport equation. The present value of the viscous superlayer thickness of $5\unicode[STIX]{x1D702}$–$6\unicode[STIX]{x1D702}$ (where $\unicode[STIX]{x1D702}$ is the Kolmogorov length scale) compares well with the values reported in the literature for other shear flows. Although both the interfaces are found to behave like a fractal with a dimension of 1.3 in two dimensions, one can find dominant length scales of the order of the thickness of the viscous superlayer, the thickness of the TNTI and the width of the mixing layer from the pre-multiplied power spectra of the autocorrelation functions of the interface curvature, the normal velocity and the interface position, along the TNTI, respectively. In addition, we find that the TNTI characteristics do not show significant dependence on the velocity ratios and $Re_{\unicode[STIX]{x1D706}}$ considered in the present study. Furthermore, the conditional transverse velocity profiles indicate that the entrainment characteristics for the upper and lower TNTIs may be asymmetric in nature.

A variational framework for the identification and analysis of general nonlinear optimal disturbances in compressible flows is derived. The formulation is based on the compressible Navier–Stokes equations in conserved variables for an ideal gas with temperature-dependent viscosity. A discretely consistent implementation based on generalized coordinates allows the accurate analysis of a wide range of settings. An application in the identification of the optimal disturbances which experience the highest amplification in kinetic energy in pipe flow is presented. At low Mach numbers and moderate initial amplitude, the disturbances undergo a sequence of Orr mechanism, oblique nonlinear interaction and lift-up mechanism, and the energy amplification is consistent with results reported for incompressible flow (Pringle & Kerswell, Phys. Rev. Lett., vol. 105, 2010, 154502). When the Mach number is increased, the gain in perturbation kinetic energy grows appreciably, and the initial disturbance field becomes increasingly localized. Nonlinear optimal disturbances which are rescaled to higher initial kinetic energy than prescribed in the optimization procedure are demonstrated to evolve into a chaotic state. For a constant time horizon, the initial perturbation energy to reach a high-energy state decreases monotonically with Mach number.

A capillary jet falling under the effect of gravity continuously stretches while thinning downstream. We report here the effect of external periodic forcing on such a spatially varying jet in the jetting regime. Surprisingly, the optimal forcing frequency producing the most unstable jet is found to be highly dependent on the forcing amplitude. Taking benefit of the one-dimensional Eggers & Dupont (J. Fluid Mech., vol. 262, 1994, pp. 205–221) equations, we investigate the case through nonlinear simulations and linear stability analysis. In the local framework, the WKBJ (Wentzel–Kramers–Brillouin–Jeffreys) formalism, established for weakly non-parallel flows, fails to capture the nonlinear simulation results quantitatively. However, in the global framework, the resolvent analysis, supplemented by a simple approximation of the required response norm inducing breakup, is shown to correctly predict the optimal forcing frequency at a given forcing amplitude and the resulting jet breakup length. The results of the resolvent analysis are found to be in good agreement with those of the nonlinear simulations.

We examine the behaviour of turbulent boundary layers over surfaces composed of spanwise-alternating smooth and rough strips, where the width of the strips $S$ varies such that $0.32\leqslant S/\overline{\unicode[STIX]{x1D6FF}}\leqslant 6.81$, where $\overline{\unicode[STIX]{x1D6FF}}$ is the boundary-layer thickness averaged over one spanwise wavelength of the heterogeneity. The experiments are configured to examine the influences of spanwise variation in wall shear stress over a large $S/\overline{\unicode[STIX]{x1D6FF}}$ range. Hot-wire anemometry and particle image velocimetry (PIV) reveal that the half-wavelength $S/\overline{\unicode[STIX]{x1D6FF}}$ governs the diameter and strength of the resulting mean secondary flows and hence the observed isovels of the mean streamwise velocity. Three possible cases are observed: limiting cases (either $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ or $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$), where the secondary flows are confined near the wall or near the roughness change, and intermediate cases ($S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$), where the secondary flows are space filling and at their strongest. These secondary flows, however, exhibit a time-dependent behaviour which might be masked by time averaging. Further analysis of the energy spectrogram and fluctuating flow fields obtained from PIV show that the secondary flows meander in a similar manner to that of large-scale structures occurring naturally in turbulence over smooth walls. The meandering of the secondary flows is a function of $S/\overline{\unicode[STIX]{x1D6FF}}$ and is most prominent when $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$.

We experimentally characterize turbulence in boundary layers generated by different levels of nearly isotropic homogeneous turbulence over flat impervious boundaries and over non-cohesive sediment beds with and without ripples. We use randomly actuated synthetic jet arrays (RASJA – Variano & Cowen, J. Fluid Mech., vol. 604, 2008, pp. 1–32) to generate high Reynolds number ($Re_{\unicode[STIX]{x1D706}}\sim 300$) turbulence with negligible secondary mean flows or mean bed shear. The isotropic region and the boundary layer connecting this isotropic region to the bed are investigated using particle image velocimetry measurements. Surprisingly, we observe the development of ripples on the sediment bed ($D_{50}=260~\unicode[STIX]{x03BC}\text{m}$). We draw comparisons between the mean shear free turbulent boundary layer formed above a flat stationary solid boundary (Johnson & Cowen, J. Fluid Mech., vol. 835, 2018, pp. 217–251) and its sediment counterpart by considering statistical metrics including root mean square velocity fluctuations, turbulent kinetic energy, dissipation rates, production, integral scales, Reynolds stresses and spatial spectra. Using an 8 × 8 RASJA, we find the damping of turbulence and dissipation rates at flat and rippled sediment beds with low levels of suspended sediments relative to an impermeable glass bed, whereas with a 16 × 16 RASJA we find the enhancement of turbulence and dissipation rates of a resuspending sediment bed relative to an impermeable glass bed. We hypothesize that this may be a result of a change in direction of the bed-normal mean flows at the porous boundary. We explore a relationship between the integral length scale of the turbulence with the resulting sediment ripple spacing by varying the mean on-time of the RASJA algorithm.

When two swimming cells collide, some ciliates show biological reactions such as avoidance and escape on sensing mechanical agitation through membrane ion channels. However, there is still no clear understanding of the mechanosensing mechanism, despite it being proposed more than 50 years ago. Moreover, it is largely unknown how the deformability of cells affects hydrodynamic interactions between microswimmers. In this study, we investigate hydrodynamic interactions between two deformable microswimmers and quantify the membrane tension during the interaction. A ciliate was modelled as a capsule with a hyperelastic membrane, and thrust generated by the cilia was modelled as torque distributed above the cell body. The model we use is the simplest we could think of that can swim, deform and exert membrane tension, such that hydrodynamic interactions can be analysed non-trivially. The results showed that softer swimmers induced smaller membrane tension during the interaction, and tended to have smaller scattering angles after the interaction. In the case of chasing interactions, swimmers attracted each other, which was not observed in non-deformable velocity squirmer models. Finally, we discuss the biological implications of these results, comparing them to those of our former experiments using Paramecium. This study is useful for understanding the effect of swimmer deformability in hydrodynamic interactions, and provides a theoretical basis for investigating a mechanical picture of the biological reactions of ciliates.

Assuming an inviscid incompressible liquid (with irrotational flows) partly filling a square base tank, which performs a small-amplitude sway/surge/pitch/roll periodic motion whose frequency is close to the lowest natural sloshing frequency, a nine-dimensional Narimanov–Moiseev-type (modal) system of ordinary differential equations with respect to the hydrodynamic generalised coordinates was derived in the Part 1 (Faltinsen et al., J. Fluid Mech., vol. 487, 2003, pp. 1–42). Constructing and analysing asymptotic periodic solutions of the system made it possible to classify steady-state resonant sloshing and its stability for the harmonic reciprocating (longitudinal, diagonal and oblique) forcing. The results were supported by experimental observations and measurements. The present paper finalises the case studies by considering the three-dimensional non-parametric (combined sway, pitch, surge, roll and yaw, but no heave) cyclic tank motions. It becomes possible after establishing an asymptotic equivalence of the associated periodic solutions of the modal system to those for a suitable horizontal translatory elliptic forcing so that, as a consequence, resonant steady-state waves and their stability can be considered versus angular position, semi-axis ratio 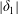$|\unicode[STIX]{x1D6FF}_{1}|$ and direction (counter- or clockwise) of the equivalent orbits. The circular orbit causes stable swirling waves (co-directed with the orbit) but may also excite stable nearly standing waves. The orbit direction does not affect the response curves for wall-symmetric (canonic) and diagonal orbit positions. This is not true for the oblique-type elliptic forcing. When the semi-axis ratio 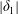$|\unicode[STIX]{x1D6FF}_{1}|$ changes from 0 to 1, the response curves exhibit astonishing metamorphoses significantly influencing the frequency ranges of stable nearly standing/swirling waves and ‘irregular’ sloshing. For the experimental input data by Ikeda et al. (J. Fluid Mech., vol. 700, 2012, pp. 304–328), the counter-directed swirling disappears as 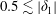$0.5\lesssim |\unicode[STIX]{x1D6FF}_{1}|$ but the frequency range of irregular waves vanishes for 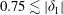$0.75\lesssim |\unicode[STIX]{x1D6FF}_{1}|$.

The interaction of motile micro-organisms with a nearby solid substrate is a well-studied phenomenon. However, the effects of hydrodynamic slippage on the substrate have received little attention. In the present study, within the framework of the squirmer model, we impose a tangential velocity at the swimmer surface as a representation of the ciliary propulsion, and subsequently obtain an exact solution of the Stokes equation based on a combined analytical–numerical approach. We illustrate how the near-wall swimming velocities are non-trivially altered by the interaction of wall slip and hydrodynamic forces. We report a characteristic transition of swimming trajectories for both puller- and pusher-type microswimmers by hydrodynamic slippage if the wall slip length crosses a critical value. In the case of puller microswimmers that are propelled by a breaststroke-like action of their swimming apparatus ahead of their cell body, the wall slip can cause wall-bound trapping swimming states, as either periodic or damped periodic oscillations, which would otherwise escape from a no-slip wall. The associated critical slip length has a non-monotonic dependence on the initial orientation of the swimmer, which is represented by novel phase diagrams. Pushers, which get their propulsive thrust from posterior flagellar action, also show similar swimming state transitions, but in this case the wall-slip-mediated reorientation dynamics and the swimming modes compete in a different fashion from that of the pullers. Although neutral swimmers lack a sufficient reorientation torque to exhibit any wall-bound trajectory, their detention time near the substrate can be significantly increased by tailoring the extent of hydrodynamic slippage at the nearby wall. The present results pave the way for understanding the motion characteristic of biological microswimmers near confinements with hydrophobic walls or strategize the design of microfluidic devices used for sorting and motion rectification of artificial swimmers by tailoring their surface wettability.

We propose a systematic methodology to derive the regularized 13-moment equations in the rarefied gas dynamics for a general class of linearized collision models. Detailed expressions of the moment equations are written down for all inverse power law models as well as the hard-sphere model. By linear analysis, we show that the equations are stable near the equilibrium. The models are tested for shock structure problems to show their capability to capture the correct flow structure in strong non-equilibrium.

We examine the critical viscous mode of the Taylor–Couette strato-rotational instability, concentrating on cases where the buoyancy frequency $N$ and the inner cylinder rotation rate $\unicode[STIX]{x1D6FA}_{in}$ are comparable, giving a detailed account for $N=\unicode[STIX]{x1D6FA}_{in}$. The ratio of the outer to the inner cylinder rotation rates $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FA}_{out}/\unicode[STIX]{x1D6FA}_{in}$ and the ratio of the inner to the outer cylinder radius $\unicode[STIX]{x1D702}=r_{in}/r_{out}$ satisfy $0<\unicode[STIX]{x1D707}<1$ and $0<\unicode[STIX]{x1D702}<1$. We find considerable variation in the structure of the mode, and the critical Reynolds number $Re_{c}$ at which the flow becomes unstable. For $N=\unicode[STIX]{x1D6FA}_{in}$, we classify different regions of the $\unicode[STIX]{x1D702}\unicode[STIX]{x1D707}$-plane by the critical viscous mode of each region. We find that there is a triple point in the $\unicode[STIX]{x1D702}\unicode[STIX]{x1D707}$-plane where three different viscous modes all onset at the same Reynolds number. We also find a discontinuous change in $Re_{c}$ along a curve in the $\unicode[STIX]{x1D702}\unicode[STIX]{x1D707}$-plane, on one side of which exist closed unstable domains where the flow can restabilise when the Reynolds number is increased. A new form of viscous instability occurring for wide gaps has been detected. We show for the first time that there is a region of the parameter space for which the critical viscous mode at the onset of instability corresponds to the inviscid radiative instability of Le Dizès & Riedinger (J. Fluid Mech., vol. 660, 2010, pp. 147–161). Focusing on small-to-moderate wavenumbers, we demonstrate that the viscous and inviscid systems are not always correlated. We explore which viscous modes relate to inviscid modes and which do not. For asymptotically large vertical wavenumbers, we have extended the inviscid analysis of Park & Billant (J. Fluid Mech., vol. 725, 2013, pp. 262–280) to cover the cases where $N$ and $\unicode[STIX]{x1D6FA}_{in}$ are comparable.

A combination of passive and active methods is used to manipulate the symmetry of the turbulent wake of an Ahmed body. Dedicated experiments to study the wake reversals occurring between symmetry-breaking states are performed. We show how transient symmetric states explored during the reversals differ from static symmetry-breaking states in the flow organization they induce. In asymmetric states, a strong interaction and coupling between the recirculating flow from one side and the shear layer from opposite side triggers shear-layer instabilities and their amplification. The resulting large-scale flow engulfment in the recirculation region increases the recirculation intensity and thus increases base drag. By contrast, during the wake reversals the disorganization of the recirculating flow leads to a transient symmetric state with prevented shear-layer interaction and triggering mechanism with a concomitant drag reduction of ${\sim}8\,\%$ compared to symmetry-breaking states. Finally, recent experimental results for unbalanced wakes and methodologies addressing the control of wake asymmetries for drag reduction are discussed and interpreted based on the present findings. This leads us to provide new insights in control methods for wake asymmetries.