Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Forooghi, Pourya
Yang, Xiang I. A.
and
Abkar, Mahdi
2020.
Roughness-induced secondary flows in stably stratified turbulent boundary layers.
Physics of Fluids,
Vol. 32,
Issue. 10,
Pandey, Anshuman
and
Gregory, James W.
2020.
Instabilities and turbulence in a forced turbulent convex wall jet.
Physics of Fluids,
Vol. 32,
Issue. 9,
von Deyn, Lars H.
Gatti, Davide
Frohnapfel, Bettina
and
Stroh, Alexander
2021.
Parametric Study on Ridges Inducing Secondary Motions in Turbulent Channel Flow.
PAMM,
Vol. 20,
Issue. 1,
Bai, Honglei
Gong, Jinlai
and
Lu, Zhenbo
2021.
Energetic structures in the turbulent boundary layer over a spanwise-heterogeneous converging/diverging riblets wall.
Physics of Fluids,
Vol. 33,
Issue. 7,
Kadivar, Mohammadreza
Tormey, David
and
McGranaghan, Gerard
2021.
A review on turbulent flow over rough surfaces: Fundamentals and theories.
International Journal of Thermofluids,
Vol. 10,
Issue. ,
p.
100077.
Nugroho, B.
Monty, J. P.
Utama, I. K. A. P.
Ganapathisubramani, B.
and
Hutchins, N.
2021.
Non--type behaviour of roughness when in-plane wavelength approaches the boundary layer thickness.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Nikitin, N. V.
Popelenskaya, N. V.
and
Stroh, A.
2021.
Prandtl’s Secondary Flows of the Second Kind. Problems of Description, Prediction, and Simulation.
Fluid Dynamics,
Vol. 56,
Issue. 4,
p.
513.
Zampiron, A.
Cameron, S.
and
Nikora, V.
2021.
Momentum and energy transfer in open-channel flow over streamwise ridges.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Zheng, Y.
and
Anderson, W.
2021.
Flow-roughness heterogeneity: critical obliquity and salient parameters.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Chung, Daniel
Hutchins, Nicholas
Schultz, Michael P.
and
Flack, Karen A.
2021.
Predicting the Drag of Rough Surfaces.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
439.
Castro, Ian P.
Kim, J.W.
Stroh, A.
and
Lim, H.C.
2021.
Channel flow with large longitudinal ribs.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Suastika, I.K.
Hakim, M.L.
Nugroho, B.
Nasirudin, A.
Utama, I.K.A.P.
Monty, J.P.
and
Ganapathisubramani, B.
2021.
Characteristics of drag due to streamwise inhomogeneous roughness.
Ocean Engineering,
Vol. 223,
Issue. ,
p.
108632.
Altland, Samuel
Zhu, Xiaowei
McClain, Stephen
Kunz, Robert
and
Yang, Xiang
2022.
Flow in additively manufactured super-rough channels.
Flow,
Vol. 2,
Issue. ,
Schäfer, Kay
Frohnapfel, Bettina
and
Mellado, Juan Pedro
2022.
The effect of spanwise heterogeneous surfaces on mixed convection in turbulent channels.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Guo, Tongbiao
Fang, Jian
Zhong, Shan
and
Moulinec, Charles
2022.
Energy-based drag decomposition analyses for a turbulent channel flow developing over convergent–divergent riblets.
Physics of Fluids,
Vol. 34,
Issue. 2,
Garcia-Mayoral, Ricardo
Durbin, Paul
McKeon, Beverley J.
Piomelli, Ugo
Sandberg, Richard D.
Bensow, Rickard
Bettle, Mark
Knopp, Tobias A.
Krumbein, Andreas
Roy, Christopher J.
Gargiulo, Aldo
Lowe, K T.
and
Toxopeus, Serge L.
2022.
Modeling of high-Re, incompressible, non-equilibrium, rough-wall boundary layers for naval applications under NATO-AVT349.
Schäfer, K.
Stroh, A.
Forooghi, P.
and
Frohnapfel, B.
2022.
Modelling spanwise heterogeneous roughness through a parametric forcing approach.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Endrikat, S.
Newton, R.
Modesti, D.
García-Mayoral, R.
Hutchins, N.
and
Chung, D.
2022.
Reorganisation of turbulence by large and spanwise-varying riblets.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Flack, Karen
and
Chung, Daniel
2022.
Important Parameters for a Predictive Model ofksfor Zero Pressure Gradient Flows.
Jelly, T.O.
Ramani, A.
Nugroho, B.
Hutchins, N.
and
Busse, A.
2022.
Impact of spanwise effective slope upon rough-wall turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
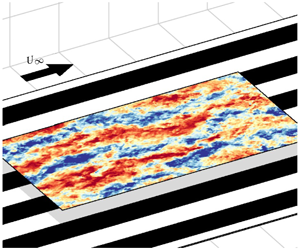
 $S$ varies such that
$S$ varies such that  $0.32\leqslant S/\overline{\unicode[STIX]{x1D6FF}}\leqslant 6.81$, where
$0.32\leqslant S/\overline{\unicode[STIX]{x1D6FF}}\leqslant 6.81$, where  $\overline{\unicode[STIX]{x1D6FF}}$ is the boundary-layer thickness averaged over one spanwise wavelength of the heterogeneity. The experiments are configured to examine the influences of spanwise variation in wall shear stress over a large
$\overline{\unicode[STIX]{x1D6FF}}$ is the boundary-layer thickness averaged over one spanwise wavelength of the heterogeneity. The experiments are configured to examine the influences of spanwise variation in wall shear stress over a large  $S/\overline{\unicode[STIX]{x1D6FF}}$ range. Hot-wire anemometry and particle image velocimetry (PIV) reveal that the half-wavelength
$S/\overline{\unicode[STIX]{x1D6FF}}$ range. Hot-wire anemometry and particle image velocimetry (PIV) reveal that the half-wavelength  $S/\overline{\unicode[STIX]{x1D6FF}}$ governs the diameter and strength of the resulting mean secondary flows and hence the observed isovels of the mean streamwise velocity. Three possible cases are observed: limiting cases (either
$S/\overline{\unicode[STIX]{x1D6FF}}$ governs the diameter and strength of the resulting mean secondary flows and hence the observed isovels of the mean streamwise velocity. Three possible cases are observed: limiting cases (either  $S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ or
$S/\overline{\unicode[STIX]{x1D6FF}}\ll 1$ or  $S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$), where the secondary flows are confined near the wall or near the roughness change, and intermediate cases (
$S/\overline{\unicode[STIX]{x1D6FF}}\gg 1$), where the secondary flows are confined near the wall or near the roughness change, and intermediate cases ( $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$), where the secondary flows are space filling and at their strongest. These secondary flows, however, exhibit a time-dependent behaviour which might be masked by time averaging. Further analysis of the energy spectrogram and fluctuating flow fields obtained from PIV show that the secondary flows meander in a similar manner to that of large-scale structures occurring naturally in turbulence over smooth walls. The meandering of the secondary flows is a function of
$S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$), where the secondary flows are space filling and at their strongest. These secondary flows, however, exhibit a time-dependent behaviour which might be masked by time averaging. Further analysis of the energy spectrogram and fluctuating flow fields obtained from PIV show that the secondary flows meander in a similar manner to that of large-scale structures occurring naturally in turbulence over smooth walls. The meandering of the secondary flows is a function of  $S/\overline{\unicode[STIX]{x1D6FF}}$ and is most prominent when
$S/\overline{\unicode[STIX]{x1D6FF}}$ and is most prominent when  $S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$.
$S/\overline{\unicode[STIX]{x1D6FF}}\approx 1$.