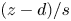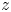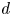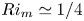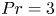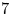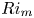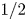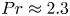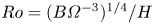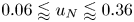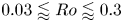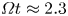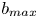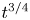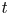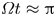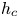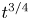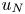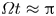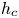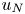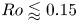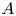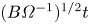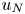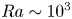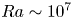Open access
JFM Papers
Regimes of soft lubrication
-
- Published online by Cambridge University Press:
- 15 March 2021, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Momentum and energy transfer in open-channel flow over streamwise ridges
-
- Published online by Cambridge University Press:
- 12 March 2021, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental evidence of internal wave attractor signatures hidden in large-amplitude multi-frequency wave fields
-
- Published online by Cambridge University Press:
- 12 March 2021, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collective locomotion of two-dimensional lattices of flapping plates. Part 1. Numerical method, single-plate case and lattice input power
-
- Published online by Cambridge University Press:
- 11 March 2021, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-periodic travelling gravity–capillary waves
-
- Published online by Cambridge University Press:
- 11 March 2021, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drift-diffusive liquid migration in partly saturated sheared granular media
-
- Published online by Cambridge University Press:
- 11 March 2021, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effects of Prandtl number on the nonlinear dynamics of Kelvin–Helmholtz instability in two dimensions
-
- Published online by Cambridge University Press:
- 11 March 2021, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steering a thermally activated micromotor with a nearby isothermal wall
-
- Published online by Cambridge University Press:
- 11 March 2021, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy, irreversibility and cascades in the inertial range of isotropic turbulence
-
- Published online by Cambridge University Press:
- 11 March 2021, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collective locomotion of two-dimensional lattices of flapping plates. Part 2. Lattice flows and propulsive efficiency
-
- Published online by Cambridge University Press:
- 11 March 2021, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Perspectives
Some topological aspects of fluid dynamics
-
- Published online by Cambridge University Press:
- 10 March 2021, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
A feedback model of the edge tone, using the adjoint Orr–Sommerfeld equation
-
- Published online by Cambridge University Press:
- 09 March 2021, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Identifying vortical network connectors for turbulent flow modification
-
- Published online by Cambridge University Press:
- 09 March 2021, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erosion-deposition dynamics and long distance propagation of granular avalanches
-
- Published online by Cambridge University Press:
- 09 March 2021, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuous hydraulic jumps in laminar channel flow
-
- Published online by Cambridge University Press:
- 09 March 2021, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Self-similar electrohydrodynamic solutions in multiple coaxial Taylor cones
-
- Published online by Cambridge University Press:
- 09 March 2021, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Turbulence properties in jets with fractal grid turbulence
-
- Published online by Cambridge University Press:
- 09 March 2021, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of background rotation on the dynamics of multiphase plumes
-
- Published online by Cambridge University Press:
- 08 March 2021, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
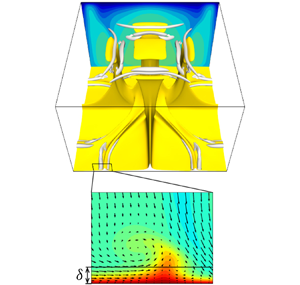
Multi-scale steady solution for Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 05 March 2021, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Editorial
Celebrating George K. Batchelor's Centenary
-
- Published online by Cambridge University Press:
- 05 March 2021, E1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation