A new model for the behaviour of a thick, two-dimensional layer of fluid on the surface of a rotating cylinder is presented, incorporating the effects of inertia, rotation, viscosity, gravity and capillarity. Comparisons against direct numerical simulations (DNS) show good accuracy for fluid layers of thickness of the same order as the cylinder radius, even for Reynolds numbers up to 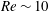 $Re\sim 10$. A rich and complex parameter space is revealed, and is elucidated via a variety of analytical and numerical techniques. At moderate rotation rates and fluid masses, the system exhibits either periodic behaviour or converges to a steady state, with the latter generally being favoured by greater masses and lower rotation rates. These behaviours, and the bifurcation structure of the transitions between them, are examined using a combination of both the low-order model and DNS. Specific attention is dedicated to newly accessible regions of parameter space, including the multiple steady state solutions observed for the same parameter values by Lopes et al. (J. Fluid Mech., vol. 835, 2018, pp. 540–574), where the corresponding triple limit point bifurcation structure is recovered by the new low-order model. We also inspect states in which the interface becomes multivalued – and thus outside the reach of the reduced-order model – via DNS. This leads to highly nonlinear multivalued periodic structures appearing at moderate thicknesses and relatively large rotation rates. Even much thicker films may eventually reach steady states (following complex early evolution), provided these are maintained by a combination of forces sufficiently large to counteract gravity.
$Re\sim 10$. A rich and complex parameter space is revealed, and is elucidated via a variety of analytical and numerical techniques. At moderate rotation rates and fluid masses, the system exhibits either periodic behaviour or converges to a steady state, with the latter generally being favoured by greater masses and lower rotation rates. These behaviours, and the bifurcation structure of the transitions between them, are examined using a combination of both the low-order model and DNS. Specific attention is dedicated to newly accessible regions of parameter space, including the multiple steady state solutions observed for the same parameter values by Lopes et al. (J. Fluid Mech., vol. 835, 2018, pp. 540–574), where the corresponding triple limit point bifurcation structure is recovered by the new low-order model. We also inspect states in which the interface becomes multivalued – and thus outside the reach of the reduced-order model – via DNS. This leads to highly nonlinear multivalued periodic structures appearing at moderate thicknesses and relatively large rotation rates. Even much thicker films may eventually reach steady states (following complex early evolution), provided these are maintained by a combination of forces sufficiently large to counteract gravity.