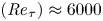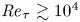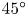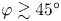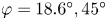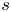Open access
JFM Papers
Buoyancy-driven instabilities of partially miscible fluids in inclined porous media
-
- Published online by Cambridge University Press:
- 14 September 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulence modulation in thermally expanding and contracting flows
-
- Published online by Cambridge University Press:
- 14 September 2021, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
One-point statistics for turbulent pipe flow up to
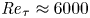 ${\textit {Re}}_{\tau } \approx 6000$
${\textit {Re}}_{\tau } \approx 6000$
-
- Published online by Cambridge University Press:
- 10 September 2021, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frequency–time analysis, low-rank reconstruction and denoising of turbulent flows using SPOD
-
- Published online by Cambridge University Press:
- 10 September 2021, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
Scale-invariant spins and tumbles in turbulence
-
- Published online by Cambridge University Press:
- 10 September 2021, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Energetics of collapsible channel flow with a nonlinear fluid-beam model
-
- Published online by Cambridge University Press:
- 09 September 2021, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Developed liquid film passing a smoothed and wedge-shaped trailing edge: small-scale analysis and the ‘teapot effect’ at large Reynolds numbers
-
- Published online by Cambridge University Press:
- 08 September 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic velocity profile causes shape-selective drift of inertial ellipsoids
-
- Published online by Cambridge University Press:
- 07 September 2021, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Designing vortices in pipe flow with topography-driven Langmuir circulation
-
- Published online by Cambridge University Press:
- 06 September 2021, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-eddy simulation and streamline coordinate analysis of flow over an axisymmetric hull
-
- Published online by Cambridge University Press:
- 06 September 2021, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A macroscopic two-length-scale model for natural convection in porous media driven by a species-concentration gradient
-
- Published online by Cambridge University Press:
- 06 September 2021, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Viscous banding instabilities: non-porous viscous fingering
-
- Published online by Cambridge University Press:
- 06 September 2021, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Crown formation from a cavitating bubble close to a free surface
-
- Published online by Cambridge University Press:
- 06 September 2021, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of front strength on the development and equilibration of symmetric instability. Part 1. Growth and saturation
-
- Published online by Cambridge University Press:
- 06 September 2021, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical analysis of a 3-D printed porous trailing edge for broadband noise reduction
-
- Published online by Cambridge University Press:
- 06 September 2021, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of front strength on the development and equilibration of symmetric instability. Part 2. Nonlinear evolution
-
- Published online by Cambridge University Press:
- 06 September 2021, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale-similar structures of homogeneous isotropic non-mirror-symmetric turbulence based on the Lagrangian closure theory
-
- Published online by Cambridge University Press:
- 06 September 2021, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparse identification of nonlinear dynamics with low-dimensionalized flow representations
-
- Published online by Cambridge University Press:
- 06 September 2021, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Imperfect symmetry of real annular combustors: beating thermoacoustic modes and heteroclinic orbits
-
- Published online by Cambridge University Press:
- 31 August 2021, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Effects of shear-thinning rheology on near-wall turbulent structures
-
- Published online by Cambridge University Press:
- 31 August 2021, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation