1. Introduction
There are numerous practical examples where the understanding of the motion of heavy particles suspended in lighter fluid is important. Typically, this will apply to any solid particle in air, commonly called aerosols. In the atmosphere, aerosols scatter light and thus also affect the global radiation budget (Holländer Reference Holländer1993). These particles also serve as condensation nuclei for cloud formation and their motion inside the clouds is important for understanding rain initiation (Balkovsky, Falkovich & Fouxon Reference Balkovsky, Falkovich and Fouxon2001; Falkovich, Fouxon & Stepanov Reference Falkovich, Fouxon and Stepanov2002) as well as snow crystal growth (Gavze, Pinsky & Khain Reference Gavze, Pinsky and Khain2012).
Closer to Earth, aerosols are typically associated with vehicle and industrial emissions causing severe health problems (Morawska & Zhang Reference Morawska and Zhang2002). Also asbestos fibres in isolation materials in buildings can be directly linked to formation of lung cancer (Miserocchi et al. Reference Miserocchi, Sancini, Mantegazza and Chiappino2008). When controlling and separating these particles from the suspending fluid, as well as understanding the deposition in the airways, it is important to find how these particles behave in channel flows. Especially important is to understand any physical process causing lateral migration of particles as this will determine if particles, for example, are concentrated in the middle of a channel or towards the walls.
Suspension flows are commonly modelled with spherical particles, due to the many models available to calculate the motion (Crowe et al. Reference Crowe, Schwarzkopf, Sommerfeld and Tsuji2012). For spherical particles it is known that inertia of the surrounding fluid can cause three types of lateral motion. Firstly, if the particle is not moving with the same velocity as the surrounding fluid, i.e. there is a slip velocity, and the particle is rotating in a constant flow without gradients, there is a lateral force on the particle called a Magnus force (Crowe et al. Reference Crowe, Schwarzkopf, Sommerfeld and Tsuji2012). Secondly, if the particle has a slip velocity and is rotating in a linear shear flow, there is a lateral force on the particle called a Saffman force (Crowe et al. Reference Crowe, Schwarzkopf, Sommerfeld and Tsuji2012). Thirdly, if the particle is suspended in a regular pipe flow, the parabolic velocity profile causes itself a migration of particles away from the centreline. As a particle move closer to the wall, the lateral migration force is balanced by pressure that is built up between the particle and the wall, causing the particle to find an equilibrium radial position in the channel. This effect is referred to as the Segré–Silberberg effect (Segré & Silberberg Reference Segré and Silberberg1961). All these effects are, however, only present when fluid inertia is relevant. If fluid inertia is negligible, which typically is true for aerosols, there is no lateral drift of spherical particles neither caused by a slip velocity nor a quadratic velocity profile.
When it comes to modelling non-spherical particles, it is common to study ellipsoids, and particularly ellipsoids with rotational symmetry called spheroids. In the absence of fluid inertia, Lamb (Reference Lamb1932) provided analytical expressions of the force on an ellipsoid in a constant flow given the orientation of the particle and Jeffery (Reference Jeffery1922) provided analytical expressions of the torque on an ellipsoid in a linear flow field. The force on a suspended inertial ellipsoid can thus be determined by the instantaneous slip velocity and the torque can be determined by local velocity gradients. The results by Jeffery (Reference Jeffery1922) have, however, mainly been used to study particles that are not affected by particle inertia and therefore will assume a rotation that gives zero torque. Lundell & Carlsson (Reference Lundell and Carlsson2010) coupled the torques by Jeffery (Reference Jeffery1922) to the equations of motion of the particle, and thus the rotational motion of an inertial particle could be simulated assuming that the surrounding flow still had zero inertia. This approach has been used in several studies using Lagrangian particle tracking (LPT) methods in e.g. turbulent channel flow with included particle inertia (e.g. Zhao et al. Reference Zhao, Challabotla, Andersson and Variano2015).
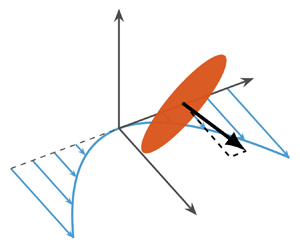
In order to analyse the particle motion, it is convenient to make a Galilean transformation to a system following the particle (see figure 1). The forces on the particle (and thus its motion) can be investigated based on the flow relative to the particle in this system. Furthermore, the decomposition of the flow seen by the particle into four fundamental flows (one of which is the parabolic velocity profile studied in the present work) is illustrated. The superposition principle of creeping (Stokes) flow implies that the total force on the particle is equal to the sum of the forces exerted by each flow alone. Thus, the effects of curvature studied in the present paper can be added to the effects of shear and homogeneous flow to study particles in all possible quadratic flows.
Figure 1. Illustration of the Galilean transformation for a particle moving in a plane Poiseuille flow. After the transformation, the particle experiences a flow that can be decomposed as shown. The effects of the different flows are additive thanks to the linearity of the Stokes equations for very viscous flow.
For the sake of discussion, we will now consider a plane laminar Poiseuille flow with a quadratic velocity profile with suspended spheroidal particles and a dilute concentration. If we were using a LPT method for determining the particle dynamics, which uses the gradient of the velocity but no higher derivatives, we would find that the particles are nicely following the straight streamlines and rotate according to the local shear given by the distance from the centreline. The orientational dynamics of the particles will then be fully determined by their behaviour in a simple shear flow. We can add both fluid and particle inertias to the rotation owing to the recent effort in mapping out the orientational behaviour of spheroids in simple shear flow (Rosén et al. Reference Rosén, Nordmark, Aidun, Do-Quang and Lundell2016). Due to the symmetry of the simple shear flow, there is no lateral drift of the spheroidal particles. Any drift must thus be caused by higher-order derivatives of the local velocity field. Chwang (Reference Chwang1975) studied the spheroidal particle with neither particle nor fluid inertia in a quadratic flow and found no lateral drift. It is still likely that inertia of the surrounding fluid will induce a Segré–Silberberg effect also for the spheroidal particles due to the parabolic velocity profile. In this work, we will show that the influence of particle inertia combined with a quadratic velocity profile will cause a lateral drift even when fluid inertia is neglected. The present results thus provide new fundamental knowledge about the migration of aerosols in channel flows.
The flow problem is defined in § 2 and the numerical method used is described in § 3. The results are presented in § 4 and discussed in § 5. Two important aspects: consequences for LPT simulations and the effect of gravity, are investigated in §§ 6 and 7, respectively. Finally the conclusions are summarized in § 8.
2. Flow problem
A prolate spheroid with major semi-axis 
$l$ is suspended in a quadratic background flow according to figure 2. The unit vectors 
$\boldsymbol {e}_1, \boldsymbol {e}_2$ and 
$\boldsymbol {e}_3$ denote the flow direction, the velocity gradient direction and the vorticity direction, respectively. The spatial coordinates are given in dimensional form as 
$\boldsymbol {x}^*=(x^*_1,x^*_2,x^*_3)$. In this work, we will mainly use the non-dimensional coordinates scaled by the particle major semi-axis, i.e. 
$\boldsymbol {x}=\boldsymbol {x}^*/l=(x_1,x_2,x_3)$. The non-dimensional coordinates of the particle centre of mass is denoted by 
$\boldsymbol {x}_{CM}$.
Figure 2. Illustration of the flow problem; a prolate spheroidal particle is suspended in a quadratic velocity profile; the position of the particle is given by the centre of mass 
$\boldsymbol {x}_{CM}$ and the orientation is given by the symmetry axis 
$\boldsymbol {s}$ and the Euler angles 
$\theta$ and 
$\phi$.
The prolate spheroidal particle with major semi-axis 
$l$ and equatorial radius 
$l/r_{p}$, where 
$r_{p}$ is the particle aspect ratio (length/width), is described through
\begin{equation} x'^{2}_1+r_{p}^2x'^{2}_2+r_{p}^2x'^{2}_3=1. \end{equation}
The non-dimensional coordinates 
$x'_1, x'_2$ and 
$x'_3$ are scaled by the major semi-axis 
$l$ and refer to the body-fixed system spanned by unit vectors 
$\boldsymbol {e}'_1, \boldsymbol {e}'_2$ and 
$\boldsymbol {e}'_3$. The orientation of the particle is given by the direction of the unit vector along the symmetry axis 
$\boldsymbol {s}$ (note that 
$\boldsymbol {s}=\boldsymbol {e}'_1$). We also express the orientation using the spherical coordinate angles 
$\theta$ and 
$\phi$ such that 
$\boldsymbol {s}=(s_1,s_2,s_3)=(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )$ according to figure 2.
The (dimensional) background flow is given by 
$\boldsymbol {u}^*_{bg}(\boldsymbol {x})=(1/2)\dot {\gamma }'l^2x_2^2\boldsymbol {e}_1$, where 
$(1/2)\dot {\gamma }'$ is the curvature of the velocity profile. The local shear rate at the particle position thus becomes 
$\dot {\gamma }_{L}(x_{CM,2}^*)=\dot {\gamma }'|x_{CM,2}^*|$. As a global time scale in this flow problem, we choose 
$\dot {\gamma }_{G}^{-1}=[\dot {\gamma }_{L}(x_{CM,2}^*=l)]^{-1}=(\dot {\gamma }'l)^{-1}$. With these spatial and temporal scalings, the non-dimensional form of the background flow becomes
\begin{equation} \boldsymbol{u}_{bg}(\boldsymbol{x})=\tfrac{1}{2}x_2^2\boldsymbol{e}_1. \end{equation}
We assume that fluid inertia is neglected, i.e. that the local particle Reynolds number 
$Re_{p,L}(x_{CM,2})=\rho _{f}\dot {\gamma }'l^3|x_{CM,2}|/\mu$ is zero (
$\rho _{f}$ is the fluid density, 
$\mu$ is the fluid dynamic viscosity), so that the flow is governed by the incompressible Stokes equations
\begin{equation} \left. \begin{array}{c@{}} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}=0,\\ \boldsymbol{\nabla} p=\nabla^2\boldsymbol{u}, \end{array}\right\} \end{equation}
where u is the fluid velocity and p is the pressure. These equations are non-dimensionalized using characteristic length 
$l$, time 
$(\dot {\gamma }'l)^{-1}$ and pressure 
$\mu \dot {\gamma }'l$. The boundary conditions of the problem are that the background flow is obtained far away from the particle, i.e.
\begin{equation} \lim_{\lvert\boldsymbol{x}\rvert \to \infty} (\boldsymbol{u}(\boldsymbol{x},t)-\boldsymbol{u}_{bg}(\boldsymbol{x}))=\boldsymbol{0}, \end{equation}
and that there is no slip of the fluid on the particle surface 
$\varGamma$, i.e.
\begin{equation} \boldsymbol{u}(\boldsymbol{x},t)=\boldsymbol{V}+\boldsymbol{\omega} \times(\boldsymbol{x}-\boldsymbol{x}_{CM}), \quad \boldsymbol{x}\in\varGamma, \end{equation}
where 
$\boldsymbol {V}$ is the (non-dimensional) velocity of the particle centre of mass located at 
$\boldsymbol {x}_{CM}$ and the (non-dimensional) particle angular velocity is 
$\boldsymbol {\omega }$. The motion of the particle is determined by the non-dimensional equations of motion
\begin{equation} \left. \begin{array}{c@{}} \boldsymbol{F}={St}_{trans.}\varPhi\dot{\boldsymbol{V}},\\ \boldsymbol{M}={St}_{rot.}[{\boldsymbol{\mathsf{I}}}\dot{\boldsymbol{\omega}}+ \boldsymbol{\omega}\times({\boldsymbol{\mathsf{I}}}\boldsymbol{\omega})], \end{array}\right\} \end{equation}
where 
$\boldsymbol {F}$ is the non-dimensional force, 
$\boldsymbol {M}$ is the non-dimensional torque and 
${\boldsymbol{\mathsf{I}}}$ is the non-dimensional inertial tensor, which are scaled by the characteristic force 
$\mu \dot {\gamma }'l^3$, torque 
$\mu \dot {\gamma }'l^4$ and inertial tensor element 
$\rho _{p} l^5$, respectively. Here, 
$\rho _{p}$ is the density of the spheroidal particle, and 
$\varPhi =(4{\rm \pi} /3) r_{p}^{-2}$ is the non-dimensional volume of the particle. In (2.6), 
${St}_{trans.}$ and 
${St}_{rot.}$ are the Stokes numbers characterizing the translational and rotational inertia of the particle, respectively. When deriving the non-dimensional equations of motion using the characteristic quantities mentioned above, these numbers will have the same value, namely
\begin{equation} {St}_{trans.}={St}_{rot.}={St}_{G}:=\frac{\rho_{p}}{\rho_{f}} Re_{p,L}(x_{CM,2}=1)=\frac{\rho_{p}\dot{\gamma}'l^3}{\mu}, \end{equation}
where 
${St}_{G}$ is called the global Stokes number. Later, in § 5.2, we will permit 
${St}_{trans.}$ and 
${St}_{rot.}$ to have separate values, but initially they will have the same value and be set according to (2.7).
Note that in order for the local Reynolds number 
$Re_{p,L}(x_{CM,2})$ to be negligible, while the local Stokes number 
${St}_{L}(x_{CM,2}):=\rho _{p}\dot {\gamma }'l^3|x_{CM,2}|/\mu$ is significant, the solid-to-fluid density ratio must fulfil 
$\rho _{p}/\rho _{f}\gg 1$. Of course, this condition will cause the particle to sediment in the presence of gravity. Initially in this study, we will neglect gravitational effects, but these will be discussed in § 7.
3. Method
3.1. Boundary integral formulation
For 
${St}_{G} > 0$, the equations of motion (2.6) are solved using Matlab's ordinary differential equation solver ode113 with relative tolerance 
$10^{-8}$. The force 
$\boldsymbol {F}$ and torque 
$\boldsymbol {M}$ are computed numerically from the position, orientation and velocity of the particle at every time step using a boundary integral formulation based on Power & Miranda (Reference Power and Miranda1987) and Gonzalez (Reference Gonzalez2009). In this formulation, the flow field in the fluid domain 
$D_{f}$ is expressed as integrals over the particle surface 
$\varGamma$
\begin{equation} \boldsymbol{u}(\boldsymbol{x},t) = \boldsymbol{\mathcal{D}}[\varGamma,\boldsymbol{q}](\boldsymbol{x}) + \boldsymbol{\mathcal{V}}[\boldsymbol{x}_{CM},\boldsymbol{F},\boldsymbol{M}]({\boldsymbol{x}}) + \boldsymbol{u}_{bg}(\boldsymbol{x}), \quad \boldsymbol{x} \in D_{f}. \end{equation}
Here, the Stokes double layer potential 
$\boldsymbol {\mathcal {D}}$ with density 
$\boldsymbol {q}$ is given by (Einstein's summation convention is used here, with all indices ranging over 
$\{1,2,3\}$)
\begin{equation} \mathcal{D}_{i}[\varGamma,\boldsymbol{q}](\boldsymbol{x}) = \int_\varGamma {\mathsf{T}}_{ijk}(\boldsymbol{x}-\boldsymbol{y}) q_j(\boldsymbol{y}) n_k(\boldsymbol{y}) \, \mathrm{d}S_{\boldsymbol{y}}, \quad {\mathsf{T}}_{ijk}(\boldsymbol{r}) ={-}6 \frac{r_ir_jr_k}{\lvert\boldsymbol{r}\rvert^5}. \end{equation}
The completion flow 
$\boldsymbol {\mathcal {V}}$ is needed to represent the force and torque, and is given by
\begin{equation} \left. \begin{array}{c@{}} \mathcal{V}_{i}[\boldsymbol{x}_{CM},\boldsymbol{F},\boldsymbol{M}](\boldsymbol{x}) = \tfrac{1}{8{\rm \pi}} ({\mathsf{C}}_{ij}(\boldsymbol{x}-\boldsymbol{x}_{CM}) F_{j} + {\mathsf{H}}_{ij}(\boldsymbol{x}-\boldsymbol{x}_{CM}) M_{j}), \\ {\mathsf{C}}_{ij}(\boldsymbol{r}) = \dfrac{\delta_{ij}}{\lvert\boldsymbol{r}\rvert} + \dfrac{r_{i}r_{j}}{\lvert\boldsymbol{r}\rvert^3}, \quad {\mathsf{H}}_{ij}(\boldsymbol{r}) = \dfrac{\varepsilon_{ijk}r_{k}}{\lvert\boldsymbol{r}\rvert^3}, \end{array}\right\} \end{equation}
where 
$\delta _{ij}$ is the Kronecker delta and 
$\varepsilon _{ijk}$ is the alternating symbol.
By letting 
$\boldsymbol {x}$ go to 
$\varGamma$ in (3.1) and using the no-slip condition together with a jump property of 
$\boldsymbol {\mathcal {D}}$, one arrives at a boundary integral equation for 
$\boldsymbol {q}$
\begin{align} -4{\rm \pi}\boldsymbol{q}(\boldsymbol{x}) + \boldsymbol{\mathcal{D}}[\varGamma,\boldsymbol{q}](\boldsymbol{x}) + \boldsymbol{\mathcal{V}}[\boldsymbol{x}_{CM},\boldsymbol{F},\boldsymbol{M}](\boldsymbol{x}) = \boldsymbol{V} + \boldsymbol{\omega} \times (\boldsymbol{x} - \boldsymbol{x}_{CM}) - \boldsymbol{u}_{bg}(\boldsymbol{x}), \quad \boldsymbol{x} \in \varGamma, \end{align}which is closed using the relations
\begin{equation} \boldsymbol{F} = \int_\varGamma \boldsymbol{q}(\boldsymbol{y}) \, \mathrm{d}S_{\boldsymbol{y}}, \quad \boldsymbol{M} = \int_\varGamma \boldsymbol{q}(\boldsymbol{y}) \times (\boldsymbol{y} - \boldsymbol{x}_{CM}) \, \mathrm{d}S_{\boldsymbol{y}}. \end{equation}For details we refer to af Klinteberg & Tornberg (Reference af Klinteberg and Tornberg2016).
For 
${St}_{G}=0$, which corresponds to a massless particle, the solution procedure is different since we know from (2.6) that 
$\boldsymbol {F} = \boldsymbol {M} = \boldsymbol {0}$. In this case, (3.4) must instead be solved for the velocities 
$\boldsymbol {V}$ and 
$\boldsymbol {\omega }$, for which relations similar to (3.5a,b) hold (see af Klinteberg & Tornberg Reference af Klinteberg and Tornberg2016).
Hence, the flow field produced by (3.1) is the solution to the Stokes equations (2.3), given that the density 
$\boldsymbol {q}$ solves (3.4).
3.2. Discretization and quadrature by expansion
The boundary integral equation (3.4) is discretized using the Nyström method (Atkinson Reference Atkinson1997, ch. 4), which enforces the equation at the grid points of the discretized particle surface, shown in figure 3. We use the trapezoidal rule with equidistant points in the periodic direction (along a circle of latitude) and an 
$n_{\theta }$-point Gauss–Legendre quadrature rule in the non-periodic direction (along a meridian). This choice gives us spectral accuracy for smooth and well-resolved integrands on the particle surface (af Klinteberg & Tornberg Reference af Klinteberg and Tornberg2016).
Figure 3. The spheroidal grid. Due to symmetry it is enough to store precomputed matrices for the 
$n_{\theta }/2$ grid points along the first half-meridian, marked with circles.
Applying the quadrature rule directly to the integral equation (3.4) is problematic for two reasons. Firstly, the integration kernel of the double layer potential (3.2a,b) is singular when the evaluation point 
$\boldsymbol {x}$ coincides with a point 
$\boldsymbol {y}$ on the boundary, and can therefore not be handled by a quadrature rule for smooth functions. Moreover, when (3.1) is evaluated in a point 
$\boldsymbol {x}$ which is close to the boundary, but not on it, the integration kernel of (3.2a,b) is sharply peaked, which causes a significant loss of accuracy close to the particle surface. We use a recent method called quadrature by expansion (QBX) to treat both of these problems. The idea behind this method is described briefly below; for a detailed description, we refer to af Klinteberg & Tornberg (Reference af Klinteberg and Tornberg2016).
QBX is based on the observation that the double layer potential 
$\boldsymbol {\mathcal {D}}$ is a smooth function away from the boundary. To avoid the problems close to the boundary, we can create a local expansion of 
$\boldsymbol {\mathcal {D}}$ around a point 
$\boldsymbol {c}$ away from the boundary. This expansion can be used to evaluate 
$\boldsymbol {\mathcal {D}}$ at exactly one point on the boundary, as shown in figure 4. To solve the integral equation we thus need one expansion centre for every grid point. Since 
$\boldsymbol {\mathcal {D}}$ has different limits from the interior and the exterior, we use both an inner and an outer expansion centre and compute the potential 
$\boldsymbol {\mathcal {D}}^{QBX}$ as an average to get the value on 
$\varGamma$.
Figure 4. (a) An expansion around a point 
$\boldsymbol {c}$ is valid within its ball of convergence of radius 
$r$ and can be used to evaluate the double layer potential at exactly one point 
$\boldsymbol {y_c}$ on the boundary. (b) For every grid point on the boundary we create an inner and an outer expansion centre.
There exist matrices 
${\boldsymbol{\mathsf{D}}}_j$ such that 
$\boldsymbol {\mathcal {D}}^{QBX}[\varGamma ,\boldsymbol {q}](\boldsymbol {x}_j) = {\boldsymbol{\mathsf{D}}}_j \boldsymbol {Q}$ for each grid point 
$\boldsymbol {x}_j$ on the surface, where 
$\boldsymbol {Q}$ is a vector containing the values of the density 
$\boldsymbol {q}$ in all grid points. The matrices 
${\boldsymbol{\mathsf{D}}}_j$ depend only on the geometry of the spheroid and can be precomputed; the result can be seen as a regular but target-specific quadrature rule. Due to rotational and mirror symmetry, it is sufficient to store matrices for the 
$n_{\theta }/2$ grid points along the first half meridian, shown in figure 3. The precomputation allows the method to be both fast and accurate, since precomputation can be done once with high accuracy and the result is reused in every time step.
3.3. Validation
The method has been validated against test cases for both inertial and massless particles, in linear shear flow and the quadratic background flow considered here. The analytical solutions in these cases are provided by Jeffery (Reference Jeffery1922) and Chwang (Reference Chwang1975); the validation is further described in Bagge (Reference Bagge2016). Using the parameters given in Appendix A, the relative errors are below 
$10^{-6}$ in all test cases.
4. Results
We start by considering a prolate spheroid of 
$r_{p}=3$ and 
${St}_{G}=50$ initialized at rest at position 
$\boldsymbol {x}_{CM}=(0,1,0)$ with a slightly oblique orientation. The trajectories of the particle translation and orientation are illustrated in figure 5. The orientation of the particle is clearly drifting towards a rotation around its minor axis, an intermittent rotation that we call tumbling. This is the same type of behaviour seen in a simple shear flow by Lundell & Carlsson (Reference Lundell and Carlsson2010). What is more striking is what is happening to the translational motion of the particle. After an initial transient the particle ends up laterally drifting towards regions of higher shear.
Figure 5. Trajectories of a particle with 
$r_{p}=3$ and 
${St}_{G}=50$, initialized at rest with an oblique orientation at 
$\boldsymbol {x}_{CM} = (0,1,0)$; (a) trajectory of centre 
$\boldsymbol {x}_{CM}$; (b) trajectory of endpoint 
$\boldsymbol {s}$, ignoring translation of the centre; (c) trajectory of endpoint including translation, i.e 
$\boldsymbol {x}_{CM}+\boldsymbol {s}$.
To quantify the observed drift, we consider a particle of 
$r_{p}=3$ that is initialized at position 
$\boldsymbol {x}_{CM}=(0,1,0)$ with velocity 
$\boldsymbol {V}=\boldsymbol {u}_{bg}(\boldsymbol {x}_{{CM}})$, aligned in the flow-gradient direction, i.e. at 
$\boldsymbol {s}=(0,1,0)$ with zero angular velocity. Note that at the given initial position, the local and global Stokes numbers are the same, i.e. 
${St}_{G}={St}_{L}(x_{CM,2}=1)$. The particle is then free to both rotate and translate up until 
$t=80$. This is repeated for a number of different 
${St}_{G}$ in the range 
${St}_{G}\in [0,100]$. The resulting trajectory of the particle centre of mass is shown in figure 6. While the spheroid with no inertia (
${St}_{G}=0$) does not show any lateral motion at all, as soon as there is particle inertia, the particle starts to migrate in positive 
$x_2$-direction, i.e. towards higher shear. Note, that the trajectories are plotted as function of the global time scale even though the local relevant time scale is changing (due to increasing local shear) with 
$x_{CM,2}$. However, this effect is negligible since the particle has not moved significantly in the 
$x_2$-direction at 
$t=80$. For all 
${St}_{G}$ studied here, the particle assumes its final state (a periodic rotation) quite quickly after an initial transient while the particle is accelerating to the surrounding flow. The final average lateral drift velocity 
$V_{drift}=\langle V_2\rangle$ for each 
${St}_{G}$ is seen to be constant, and is estimated by fitting a linear function to 
$x_{{CM},2}(t)$ between times 
$t=20$ and 
$80$ as seen by the dashed lines in figure 6. From the figure it is also evident that there is a critical Stokes number 
${St}_{c}\approx 30$ such that 
$V_{drift}$ has a maximum value when 
${St}_{G}={St}_{c}$. At 
${St}_{G}\leq 30$ (figure 6a) the drift velocity 
$V_{drift}$ is increasing with 
${St}_{G}$ while at 
${St}_{G}\geq 30$ (figure 6b), 
$V_{drift}$ is decreasing with 
${St}_{G}$.
Figure 6. Illustration of the inertial drift of a particle with 
$r_{p}=3$ at (a) 
${St}_{G} \leq 30$ and (b) 
${St}_{G} \geq 30$. Dashed lines indicate average (fitted) slopes.
Considering now a particle with different aspect ratios 
$r_{p}=1,2,3,4$ at 
${St}_{G}=50$ in figure 7(a), we find that a spherical particle, as expected, has no lateral drift. As soon as the particle gets a prolate shape, it gets a constant drift velocity, which at 
${St}_{G}=50$ is increasing with 
$r_{p}$. In figure 7(b), the final drift velocity 
$V_{drift}$ is plotted as function of 
${St}_{G}$ for the different 
$r_{p}$ and we find that both the maximum 
$V_{drift,max}$ and the Stokes number 
${St}_{c}$ where this occurs are indeed increasing with 
$r_{p}$.
Figure 7. Inertial drift velocity 
$V_{drift}$ as a function of aspect ratio 
$r_{p}$; (a) position vs time; (b) 
$V_{drift}$ vs 
${St}_{G}$ at various 
$r_{p}$.
As previously mentioned, if we would release the particle at different heights 
$x_{CM,2}$ in the flow, the particle would experience different shear rates and the relevant time scale would change. In this case the local 
${St}_{L}=|x_{CM,2}|{St}_{G}$ depends on lateral position in the flow, which in turn determines the drift velocity. To demonstrate this, we released the particle of 
$r_{p}=3$ at two more locations 
$x_{CM,2}=1/2$ and 
$x_{CM,2}=2$. We can see in figure 8(a) that 
$V_{drift}$ is only dependent on 
${St}_{L}$ as all the curves collapse when the velocity is plotted vs this parameter. Consequently, there will always be a particle position in the channel 
$x_{CM,2}=x_{CM,2,c}$ where we have a maximum drift velocity, which is where 
${St}_{L}(x_{CM,2,c})={St}_{c}$. If we e.g. start at 
$|x_{CM,2}|<1$, we will always eventually reach this position since the particle is drifting towards regions of higher shear. Eventually, the drift will vanish as 
${St}_{L}\rightarrow \infty$, which is demonstrated in figure 8(b) where the results of 
$V_{drift}$ at very high 
${St}_{L}$ are illustrated.
Figure 8. (a) The drift velocity 
$V_{drift}$ as a function of local 
${St}_{L}(x_{CM,2})$ for different initial heights and 
$r_p=3$; figure shows that 
$V_{drift}$ is only dependent on the local 
${St}_{L}(x_{CM,2})$, with a maximum at 
${St}_{L}(x_{CM,2,c}) = {St}_{c}$; (b) the drift velocity 
$V_{drift}$ at very high values of 
${St}_{L}$.
5. Discussion
The previous section has shown the results that particle inertia is sufficient to cause a lateral drift of a particle in a quadratic velocity profile. The source of the resulting translational and rotational motion will be discussed in this section.
5.1. Without inertia
Jeffery (Reference Jeffery1922) and Lamb (Reference Lamb1932) present expressions for the force 
$\boldsymbol {F}_0$ and torque 
$\boldsymbol {M}_0$ on a translating and rotating spheroidal particle in a quiescent fluid, while Chwang (Reference Chwang1975) derived expressions for the force 
$\boldsymbol {F}^{Chw}$ and torque 
$\boldsymbol {M}^{Chw}$ on a non-translating and non-rotating spheroidal particle in a paraboloidal velocity profile. One important thing to note is that the results by Chwang (Reference Chwang1975) were derived for a paraboloidal profile 
$\boldsymbol {u}^{Chw}_{bg}(\boldsymbol {x})=(1/2)(x_2^2+x_3^2)\boldsymbol {e}_1$. By adjusting these results, we can express the force 
$\boldsymbol {F}^{par}$ and torque 
$\boldsymbol {M}^{par}$ valid for the parabolic background velocity profile considered here 
$\boldsymbol {u}_{bg}(\boldsymbol {x})=(1/2)x_2^2\boldsymbol {e}_1$. This derivation is given in Appendix B (it turns out that the torque is the same in both cases, 
$\boldsymbol {M}^{par} = \boldsymbol {M}^{Chw}$).
Through the principle of superposition, the total force and torque on a moving and rotating spheroidal particle in a parabolic velocity profile in the absence of fluid inertia can be found by combining the adjusted results by Chwang (Reference Chwang1975) with the expressions of Jeffery (Reference Jeffery1922) and Lamb (Reference Lamb1932), i.e. 
$\boldsymbol {F}=\boldsymbol {F}_0+\boldsymbol {F}^{par}$ and 
$\boldsymbol {M}=\boldsymbol {M}_0+\boldsymbol {M}^{par}$. If we want to study the free motion of the spheroid with no particle inertia (
${St}_{trans.}={St}_{rot.}=0$ in (2.6)), the resulting force 
$\boldsymbol {F}$ and torque 
$\boldsymbol {M}$ are set to zero.
5.1.1. Rotation without inertia
Let us now consider a particle that is oriented in the flow-gradient plane (
$\theta ={\rm \pi} /2$). The torque on a spheroidal particle rotating in the flow-gradient plane with angular velocity 
$\dot {\phi }$ in a quiescent fluid is given in non-dimensional form by Jeffery (Reference Jeffery1922) as
\begin{equation} \boldsymbol{M}_0(\dot{\phi}) ={-}\frac{16{\rm \pi}}{3} \frac{r_{p}^2 + 1}{K_1 r_{p}^2 + K_2} \dot{\phi} \boldsymbol{e}'_2, \end{equation}where
\begin{equation} K_1 = \int_0^\infty \frac{\mathrm{d}\beta}{(1+\beta)^{3/2}(r_{p}^{{-}2} + \beta)}, \quad K_2 = \int_0^\infty \frac{\mathrm{d}\beta}{(1+\beta)^{1/2}(r_{p}^{{-}2} + \beta)^2}. \end{equation}
The torque on a stationary particle with orientation 
$\phi$ and location 
$\boldsymbol {x}_{CM}$ in a parabolic velocity profile is given through the (non-dimensional) expression by Chwang (Reference Chwang1975) as
\begin{equation} \boldsymbol{M}^{par}(\phi,\boldsymbol{x}_{CM})={-}\frac{32{\rm \pi}}{3} \frac{E^3 (1 - E^2 \cos^2 \phi)}{-2E+(1+E^2) \log[(1+E)/(1-E)]} x_{{CM},2} \boldsymbol{e}'_2, \end{equation}
where 
$E = \sqrt {1-r_{p}^{-2}}$ is the eccentricity of the spheroid.
The total torque on the particle rotating arbitrarily in a parabolic velocity profile is given by 
$\boldsymbol {M}=\boldsymbol {M}_0+\boldsymbol {M}^{par}$. The resulting expression is actually exactly equivalent to the expression by Jeffery (Reference Jeffery1922) in a linear shear flow. The conclusion drawn already by Chwang (Reference Chwang1975) is thus that the quadratic terms in the background flow do not affect the particle rotation. Consequently, the particle without rotational inertia (
${St}_{rot.}=0$), which rotates according to the solution of 
$\boldsymbol {M}=\boldsymbol {0}$, will just rotate according to the local shear rate in an intermittent tumbling motion described by Jeffery (Reference Jeffery1922) as
\begin{equation} \dot{\phi}(\phi,\boldsymbol{x}_{CM}) = |x_{{CM},2}| \frac{r_{p}^2 \sin^2 \phi + \cos^2 \phi}{r_{p}^2+1}. \end{equation}The rotational period is given by
\begin{equation} T_J=\frac{2{\rm \pi}}{|x_{CM,2}|}(r_p+r_p^{{-}1}). \end{equation}5.1.2. Translation
The force on a spheroidal particle moving with instantaneous velocity 
$\boldsymbol {V}$ and orientation 
$\phi$ in a quiescent fluid is given by Lamb (Reference Lamb1932) as
\begin{equation} \boldsymbol{F}_0(\boldsymbol{V},\phi)={-}16{\rm \pi} {\boldsymbol{\mathsf{K}}}(\phi)\boldsymbol{V}, \end{equation}
where the tensor 
${\boldsymbol{\mathsf{K}}}$ in the body-fixed coordinate system (equivalent to 
$\phi =0$) is given by
\begin{equation} {\boldsymbol{\mathsf{K}}}(0) = \left(\begin{matrix} (K_0+K_1)^{{-}1} & 0 & 0 \\ 0 & (K_0+K_2 r_{p}^{{-}2})^{{-}1} & 0 \\ 0 & 0 & (K_0+K_2 r_{p}^{{-}2})^{{-}1} \end{matrix} \right), \end{equation}with
\begin{equation} K_0 = \int_0^\infty \frac{\mathrm{d}\beta}{(1+\beta)^{1/2}(r_{p}^{{-}2} + \beta)}. \end{equation}
If 
$\phi \neq 0$, the tensor will simply be transformed according to 
${\boldsymbol{\mathsf{K}}}(\phi )={\boldsymbol{\mathsf{R}}}(\phi ){\boldsymbol{\mathsf{K}}}(0){\boldsymbol{\mathsf{R}}}^{-1}(\phi )$ with the rotation matrix 
${\boldsymbol{\mathsf{R}}}$.
The force on a stationary particle with orientation 
$\phi$ (between 
$\boldsymbol {s}$ and 
$\boldsymbol {u}_{CM}$) and location 
$\boldsymbol {x}_{CM}$ in a parabolic velocity profile is given through the adjusted expression by Chwang (Reference Chwang1975) (see Appendix B) as
\begin{align} \boldsymbol{F}^{par}(\phi,\boldsymbol{x}_{CM}) &= \frac{8 {\rm \pi}E^3 \cos \phi}{3} \frac{3 x_{{CM},2}^2 + 1 - E^2 \cos^2 \phi}{-2E + (1+E^2) \log[(1+E)/(1-E)]} \boldsymbol{e}'_1 \nonumber\\ &\quad - \frac{16{\rm \pi} E^3 \sin \phi}{3} \frac{3 x_{{CM},2}^2 + 1 - E^2 \cos^2 \phi}{2E + (3E^2-1) \log[(1+E)/(1-E)]} \boldsymbol{e}'_2. \end{align}
The total force on the particle arbitrarily translating and rotating in a parabolic velocity profile is given by 
$\boldsymbol {F}=\boldsymbol {F}_0+\boldsymbol {F}^{par}$. If the particle is oriented with an angle 
$\phi$ and free to translate in the absence of translational inertia (
${St}_{trans.}=0$), the velocity that satisfies 
$\boldsymbol {F}=\boldsymbol {0}$ is given by
\begin{equation} \boldsymbol{V}(\phi,\boldsymbol{x}_{CM}) = \tfrac{1}{6} ( 3 x_{{CM},2}^2 + 1 - E^2 \cos^2 \phi ) \boldsymbol{e}_1. \end{equation}
The particle has a velocity in the flow direction, which depends on the instantaneous angle 
$\phi$. If the particle is free to rotate without rotational inertia, it will perform an intermittent tumbling motion according to (5.4). Consequently, this thus results in an intermittent translational motion in the flow direction.
5.2. Adding inertia
5.2.1. Only rotational inertia
Although not easily achievable in practice, let us now consider the case where 
${St}_{rot.}>0$ but translational inertia is neglected 
${St}_{trans.}=0$. Since we know from the expressions above that the translational motion is only in the flow direction in the absence of translational inertia and the rotational motion is only dependent on the motion in the gradient direction, the translation will not influence the particle rotation. With added rotational inertia, the particle will thus behave exactly according to Lundell & Carlsson (Reference Lundell and Carlsson2010), where the instantaneous torque during the final rotational motion typically is non-zero but fulfils 
$\int _0^T \boldsymbol {M} \mathrm {d}t=\boldsymbol {0}$ for the rotational period 
$T$. At extremely large 
${St}_{rot.}\rightarrow \infty$, the particle will rotate with a constant angular velocity 
$\dot {\phi }=-0.5|x_{CM,2}|$ and period 
$T_H=4{\rm \pi} /(|x_{CM,2}|)$ as the particle inertial forces overcome viscous forces from the surrounding fluid. A critical rotational Stokes number 
${St}_{0.5}$ was introduced by Lundell & Carlsson (Reference Lundell and Carlsson2010) to describe the transition. This number is defined as the 
${St}_{rot.}$ where the tumbling period is 
$T=(T_J+T_H)/2$. With corrections given by Nilsen & Andersson (Reference Nilsen and Andersson2013), this number can be found through
\begin{equation} {St}_{0.5}=\frac{20[0.7+0.3[1-\varepsilon^2]^{5/8})]}{\varLambda[K_1+\varLambda K_2]}, \end{equation}with
\begin{equation} \varepsilon=\frac{r_{p}^{2}-1}{r_{p}^{2}+1}, \quad \varLambda=\frac{1-\varepsilon}{1+\varepsilon}. \end{equation}
Lundell & Carlsson (Reference Lundell and Carlsson2010) also found that the particle initially oriented out of the flow-gradient plane always still drifted towards the tumbling motion due to the centrifugal forces on the particle. The rate of this orbit drift was seen to be close to maximum when 
${St}_{rot.}={St}_{0.5}$. Interestingly, the critical rotational Stokes number 
${St}_{0.5}$ for maximum orbit drift seems to scale similarly with aspect ratio as the critical translational Stokes number 
${St}_{c}$ for the lateral drift as illustrated in figure 9. This indicates that the maximum lateral drift also arises in the transition when inertial forces overcome viscous damping.
Figure 9. The critical Stokes numbers 
${St}_{c}$ and 
${St}_{0.5}$ as functions of 
$r_{p}$.
The fact that the instantaneous torque on the particle is exactly represented by the solutions by Jeffery (Reference Jeffery1922) is also confirmed by the Stokes flow simulations in the present work. In figure 10, we plot the torque 
$M_3$ on the particle as a function of orientation 
$\phi$ and angular velocity 
$\dot {\phi }$. Furthermore, we superimpose the trajectories of the numerical simulations from our results at higher 
${St}_{L}={St}_{rot.}={St}_{trans.}$. Here, we can clearly see how the particle travels through regions of both positive and negative torque during a rotation and approaching constant angular velocity 
$\dot {\phi }=-0.5|x_{CM,2}|$ as 
${St}_{L}$ increases. We find in the numerical simulations also that the translational inertia has no effect on the rotation, except for the fact that the lateral drift changes the local time scale (through the local shear rate) and thus also the local Stokes number 
${St}_{L}$.
Figure 10. Torque 
$M_3$ given on a particle (
$r_{p}=3$) in a quadratic flow at 
$x_{CM,2}=1$ with no translational velocity in a tumbling orbit (
$s_3=\cos \theta =0$) as function of orientation 
$\phi$ and angular velocity 
$\dot {\phi }$; the solid, dashed and dotted lines show the superimposed path of a particle that is free to translate at 
${St}_{L} = 0, 50$ and 
$100$, respectively.
5.2.2. Adding translational inertia
With no translational inertia, the particle moves with oscillating 
$V_1$-velocity (
$V_2=0$) corresponding to 
$\boldsymbol {F}=\boldsymbol {0}$. The oscillation period corresponds to the oscillation period of 
$\phi$.
With added rotational inertia (still no translational inertia) as we observed previously, there will be a different oscillation period, but 
$V_1$ is still given by the 
$\boldsymbol {F}=\boldsymbol {0}$ solution, which does not imply any lateral drift (
$V_2=0$). With added translational inertia (no rotational inertia) the particle will be slow to react to the forces and the particle will typically experience non-zero forces but eventually leading to a translational motion that fulfils 
$\int _0^T \boldsymbol {F} \, \mathrm {d}t=\boldsymbol {0}$. This solution actually has 
$V_2\neq 0$ and the particle will drift laterally.
With added rotational inertia, the oscillation period of the velocity will decrease as the oscillation period of 
$\phi$ will decrease. The fact that the instantaneous force on the particle is exactly represented by the analytical expressions of 
$\boldsymbol {F}=\boldsymbol {F}_0+\boldsymbol {F}^{par}$ is confirmed in the present Stokes flow simulations. In figure 11, we illustrate the instantaneous forces parallel (
$F_1$) and normal (
$F_2$) to the flow, for a given orientation 
$\phi$ and streamwise velocity difference 
$V_1-u_{{bg},1}(x_{{CM},2})$. Superimposed, we again plot the trajectories of the numerical Stokes flow simulations at higher 
${St}_{L}={St}_{rot.}={St}_{trans.}$. Here, we can again observe how the particle travels through regions of positive and negative forces, and that the velocity oscillations will decrease in amplitude and approach a constant velocity as 
${St}_{L}$ is increased.
Figure 11. Forces given on a particle (
$r_p=3$) with fixed orientations of a tumbling orbit (
$s_3=\cos \theta =0$) as functions of orientation 
$\phi$ and streamwise velocity 
$V_1$; the solid, dashed and dotted lines show the superimposed path of a particle that is free to translate at 
${St}_{L} = 0, 50$ and 
$100$, respectively: (a) force component 
$F_1$ parallel to flow; (b) force component 
$F_2$ normal to flow.
To really conclude what is causing the drift, additional simulations were performed where 
${St}_{trans.}$ was varied independently from 
${St}_{rot.}$. The resulting drift velocities 
$V_{drift}$ after the initial transient are summarized in table 1. It is found that 
$V_{drift}$ is mainly dependent on the translational inertia of the particle. Even though the oscillation period changes, the effect of 
${St}_{rot.}$ at a constant 
${St}_{trans.}$ is almost negligible.
Table 1. The final lateral velocity 
$V_{drift}$ for different combinations of 
${St}_{trans.}$ and 
${St}_{rot.}$ for a particle with 
$r_p=3$.
It is also quite clear what will happen with oblate spheroids. Since the inertial oblate spheroid will drift towards a rotation around its symmetry axis, there will be no ‘jerk’ in the translational motion, the force will be the same regardless of rotational phase and the particle will assume the velocity corresponding to zero force. There will thus not be any lateral motion for oblate particles.
5.3. Additional remark
The present results of the numerical Stokes flow simulations have demonstrated that the flow problem can be completely analysed analytically by integrating the equations of motion (2.6) using the force and torque expressions by Jeffery (Reference Jeffery1922) and Lamb (Reference Lamb1932) and the modified expressions by Chwang (Reference Chwang1975) in (5.1)–(5.3) and (5.6)–(5.9). The QBX method, however, can be utilized in the future for more complicated flow problems, e.g. including complex geometries, where analytical solutions are difficult to obtain.
6. Consequences for simulations with Lagrangian particles
The fact that there is an additional force that arises from the second spatial derivative of the velocity also has consequences for LPT methods. In these schemes, the force on the particle is calculated by knowing the (dimensional) velocity difference 
${\rm \Delta} \boldsymbol {U}^*=\boldsymbol {u}^*_{CM}-\boldsymbol {V}^*$ between the particle and the undisturbed fluid. Similarly, the torque is found only through the orientation and the local velocity gradients, i.e. the first spatial derivatives of the velocity. The second spatial derivative was seen here to only affect the translation and not the rotation. So how can we evaluate if this contribution to the force is relevant?
Consider a particle in a Lagrangian frame centred on the particle with flow direction 
$\boldsymbol {e}_1$ and gradient direction 
$\boldsymbol {e}_2$ with constant curvature of the velocity profile given by 
$\dot {\gamma }'$. The particle experiences the velocity 
${\rm \Delta} \boldsymbol {U}^*$ and will thus have dimensional force contribution according to Lamb (Reference Lamb1932) as
\begin{equation} \boldsymbol{F}^*_{{\rm \Delta} U}=16{\rm \pi} \mu l {\boldsymbol{\mathsf{K}}}(\phi){\rm \Delta} \boldsymbol{U}^*. \end{equation}
Since the Lagrangian frame is always centred on the particle, the force contribution due to the second spatial derivative of the velocity will be equivalent to setting 
$x_{{CM},2}=0$ in (5.9). The dimensional result thus becomes
\begin{align} \boldsymbol{F}^*_{curv.}&= 16{\rm \pi} \mu l \dot{\gamma}' l^2 \frac{1-E^2\cos^2\phi}{3}\left(\cos\phi\frac{\boldsymbol{e}'_1}{2A_1}- \sin\phi\frac{\boldsymbol{e}'_2}{A_2}\right)\nonumber\\ &= 16{\rm \pi} \mu l \dot{\gamma}' l^2 \frac{1-E^2\cos^2\phi}{3} {\boldsymbol{\mathsf{K}}}(\phi)\boldsymbol{e}_1, \end{align}
where 
$A_1=(-2E + (1+E^2) \log [(1+E)/(1-E)])/E^3$ and 
$A_2=(2E + (3E^2-1) \log [(1+E)/(1-E)])/E^3$ are parameters determined by the particle geometry. Furthermore, all geometry dependent parameters 
${\boldsymbol{\mathsf{K}}}, E, A_1$ and 
$A_2$ are 
$\textit {O}(1)$ for moderate aspect ratios. In order to neglect the contribution of the velocity curvature in an LPT simulation when calculating the force, the condition 
$|\dot {\gamma }'|l^2/|{\rm \Delta} \boldsymbol {U}^*|\ll 1$ should thus hold.
As a final remark, it is likely that there is a similar correction to the rotation by taking into account the third spatial derivative of the velocity.
7. Effects of gravity
In order to determine to what extent the drift mechanism scrutinized above will be relevant in a physically realizable system on Earth, it must be compared with the effect of gravity. For inertial particles in Stokes flow, gravity can induce a sideways drift already under the assumption of linear shear (without curvature), shown by Broday et al. (Reference Broday, Fichman, Shapiro and Gutfinger1998). This drift appears since oblique particles sediment sideways and intermediate inertia gives non-symmetric angular distributions.
In figure 12, the effect of gravity is investigated. In (a) and (b), the particle motion is shown at different levels of non-dimensional gravitational force
\begin{equation} g = \frac{\rho_{p} \varPhi G}{\mu \dot{\gamma}'}, \end{equation}
where 
$G$ is the physical (dimensional) gravitational acceleration, and the other parameters are as introduced in § 2. The particle motion is shown for aspect ratio 
$r_{p}=3$ and Stokes number 
${St}_{G}=30$ (at which the curvature-induced drift is approximately maximal for this aspect ratio). From the particle motions, the sideway drift can be determined as a function of 
$g$, as shown in (c,d). Due to the curvature-induced drift, the net drift is not 0 for 
$g=0$. In fact, for aspect ratio 
$r_{p}=3$, the curvature-induced drift is seen to dominate for 
$\lvert g \rvert <0.014$ with gravity normal to the flow direction and 
$\lvert g \rvert < 0.72$ for gravity parallel to the flow direction. The critical gravities for other aspect ratios are shown in table 2.
Figure 12. (a,b) Particle motion for a particle with 
$r_{p}=3, {St}_{G}=30$ and gravity parallel (a) and normal (b) to the flow direction. In (c,d), the sideways drift, obtained from the slopes indicated with dashed lines in (a,b), is shown as a function of non-dimensional gravity 
$g$ for both directions of gravity. Magnifications of the neighbourhood around 
$g=0$ are shown as insets.
Table 2. Critical gravities and particle half-lengths for different aspect ratios 
$r_{p}$ at the Stokes number 
${St}_{G}$ inducing close to maximal drift. Columns 3–4 show the critical gravity (defined as the gravity yielding zero drift velocity, cf. figure 12(c,d) with gravity acting parallel and normal to the flow direction, respectively. Column 5 shows the particle half-length corresponding to 
$g=g_{{crit},\parallel }, \rho _{p}=1000$ kg m
$^{-3}$ and 
$G=10$ m s
$^{-2}$ in (7.5). Column 6 shows the corresponding Reynolds number due to sedimentation, from (7.6).
The question which immediately follows is under what conditions 
$\lvert g \rvert < 0.72$ can be obtained. Simultaneously, the Reynolds number
\begin{equation} \textit{Re}_{sed}=\frac{\rho_{f} U_{sed} l}{\mu}, \end{equation}
due to sedimentation must be small for the creeping condition to be satisfied. The sedimentation velocity 
$U_{sed}$ is estimated from the vertical force balance between buoyancy and gravity (cf. (6.1)), assuming 
${\boldsymbol{\mathsf{K}}}$ to be of 
$O(10)$ (this has been verified numerically)
\begin{equation} (\rho_{p}-\rho_{f}) \varPhi l^3 G \approx 160{\rm \pi}\mu l U_{sed}. \end{equation}
Assuming 
$\rho _{f} \ll \rho _{p}$ and inserting the non-dimensional volume 
$\varPhi = (4{\rm \pi} /3)r_{p}^{-2}$ of a spheroid, as well as the definition (2.7) of 
${St}_{G}$, the above equations can be rearranged to give
\begin{equation} \textit{Re}_{sed} \approx \frac{\rho_{p}\rho_{f} l^3 G}{120\mu^2 r_{p}^2}, \end{equation}and
\begin{equation} g = \frac{4 {\rm \pi}\rho_{p}^2 l^3 G}{3r_{p}^2 \mu^2 {St}_{G}}. \end{equation}
Note that both 
$g$ and 
$\textit {Re}_{sed}$ are functions of 
$l^3 G$. Solving (7.5) for 
$l^3 G$ and inserting into (7.4) yields
\begin{equation} \textit{Re}_{sed} \approx \frac{\rho_{f} {St}_{G} g}{160 {\rm \pi}\rho_{p}}. \end{equation} With the fluid taken as air at normal conditions (
$\mu =1.8\times 10^{-5}$ Pa s, 
$\rho _{f}=1.2$ kg m
$^{-3}$) and considering the case 
$r_{p}=3, {St}_{G}=30$, the relations (7.5) and (7.6) can be summarized as in figure 13. In (a), the critical gravitational acceleration 
$G$ (corresponding to 
$g=g_{{crit},\parallel }=0.72$) is shown as a function of 
$l$ for different particle densities 
$\rho _{p}$. The critical 
$G$ is less than the approximately 10 m s
$^{-2}$ that we have on the surface of Earth, except for small particles (e.g. 
$l=10\ \mathrm {\mu }$m, 
$\rho _{p}=1000$ kg m
$^{-3}$). For heavier and larger particles, lower levels of gravity, such as on the international space station, are necessary for the curvature-induced drift to dominate over gravity. In figure 13(b), 
$\textit {Re}_{sed}$ at the critical gravity 
$g_{{crit},\parallel }$ is shown as a function of 
$\rho _{p}$. Since 
$\textit {Re}_{sed} \ll 1$ for all 
$\rho _{p}$ shown, the creeping flow condition is not violated for the conditions in (a).
Figure 13. (a) Critical value of the gravitational acceleration 
$G$ as a function of particle size 
$l$ (cf. (7.5) with 
$g=g_{{crit},\parallel }$). The solid lines are 
$r_{p}=3$ and 
$\rho _{p}=100$, 1000 and 10000 kg m
$^{-3}$ for blue, red and yellow, respectively. The dash-dotted line is 
$r_{p}=10$, 
$\rho _{p}=1000$ kg m
$^{-3}$. The new drift mechanism dominates below the lines. The horizontal black line indicates 
$G=10$ m s
$^{-2}$. (b) 
$Re_{sed}$ at the critical gravity 
$g_{{crit},\parallel }$ as a function of 
$\rho _{p}$ (cf. (7.6) with 
$g=g_{{crit},\parallel }$). The lines are 
$r_{p}=3$ (blue) and 
$r_{p}=10$ (red).
8. Conclusions
In this work we have investigated a new shape-selective drift mechanism which applies to inertial prolate ellipsoidal particles in a parabolic velocity profile. The results are derived with the assumption that inertia of the fluid flow around the particle is negligible. The work can thus be viewed as a direct continuation of the work by Chwang (Reference Chwang1975) to account for particle inertia.
It is found that non-sphericity, particle inertia and the quadratic profile contribute to a lateral drift towards regions of higher shear. The particle inertial effects are governed by the local Stokes number 
${St}_{L}$ based on the local shear rate. In the absence of inertia (
${St}_{L}=0$), when the particle is aligned in the flow-gradient plane, it assumes an intermittent tumbling motion where the angular velocity depends on the angle. This intermittent rotation is determined only by the local shear rate and described in detail by Jeffery (Reference Jeffery1922). This causes the particle in the parabolic profile to have an intermittent streamwise velocity depending on the instantaneous orientation (Chwang Reference Chwang1975).
With higher 
${St}_{L}$, the particle behaves exactly as expected in a linear shear flow according to the results by Lundell & Carlsson (Reference Lundell and Carlsson2010). However, due to its translational inertia, the particle is not quick enough to adapt to the non-zero forces during a particle rotation. The final trajectory of the particle, when the impulse during a rotational period is zero, describes a translational motion with a lateral drift. At very high 
${St}_{L}$, the particle will approach a rotation with constant angular velocity and also a translation with constant velocity, and the lateral drift vanishes.
If the particle is not initially oriented in the flow-gradient plane it will drift towards such an orbit. Since the particle is seen to have angular dynamics which are identical to a particle in simple shear, we know from Lundell & Carlsson (Reference Lundell and Carlsson2010) that the maximum orbit drift occurs at 
${St}_{L}\approx {St}_{0.5}$. The critical value of 
${St}_{0.5}$ is defined when particle inertia overcomes viscous damping and can be found analytically, see (5.11). We find furthermore that this critical number also predicts when we can expect the maximum lateral drift. Since the particle tends to migrate towards regions of larger shear, we know that a particle released at a position where 
${St}_{L}<{St}_{0.5}$ will reach both a position where 
${St}_{L}\approx {St}_{0.5}$ with a maximum drift angle (angle between particle velocity and flow direction) and later have a decreasing drift angle as the particle migrates further in the lateral direction.
The maximum lateral drift velocity was found to be dependent on the particle aspect ratio, with higher drift for larger aspect ratio 
$r_{p}$. However, since the intermittent tumbling motion is essential to have this type of drift, inertial oblate particles and spheres (
$r_{p}\leq 1$) are not affected by this drift since they preferably rotate in a non-intermittent state.
Although the results were found through simulations of the Stokes flow using the numerical QBX method, it is found that the forces and torques on the particle are exactly represented by the analytical expressions by Lamb (Reference Lamb1932) and the modified expressions of Chwang (Reference Chwang1975) (with modifications presented in Appendix B). This means that the equations of translational and rotational motion can be directly integrated using these expressions to arrive at the same conclusions as in the present work. The strength in the QBX method lies mainly in the fact that we can additionally use the same method for studying other flow problems where analytical solutions are more difficult to obtain, for example having multiple particles and wall-bounded flow through complex geometries.
In LPT methods, the force on the particle is usually calculated using only the instantaneous velocity difference 
${\rm \Delta} \boldsymbol {U}^*$ between the particle and the undisturbed fluid. Here, it is demonstrated that there is also a contribution to the force from the curvature of the velocity profile 
$\dot {\gamma }'$, and that 
$|\dot {\gamma }'|l^2/|{\rm \Delta} \boldsymbol {U}^*|\ll 1$ must hold for this contribution to be negligible.
Finally, it is known from recent work (e.g. Einarsson et al. Reference Einarsson, Candelier, Lundell, Angilella and Mehlig2015a,Reference Einarsson, Candelier, Lundell, Angilella and Mehligb) that fluid inertial effects are dominating over particle inertial effects for spheroidal particles of same density as the surrounding fluid. The consequence is that we can only neglect fluid inertia, if the local Stokes number 
${St}_{L}$ is much larger than the local Reynolds number 
$Re_{p,L}\ll 1$, i.e. the solid-to-fluid density ratio must be large. In the presence of gravity this will cause the particles to sediment, and we proceeded to investigate under what circumstances the new drift would dominate over gravitational effects. We find that the new drift is more likely to dominate when particles are small and light, and when the flow is vertical, i.e. parallel to the direction of gravity. As an example, on Earth, particles of density 1000 kg m
$^{-3}$ moving through air would need to be smaller than around 10 
$\mathrm {\mu }$m for the new drift to be able to dominate over gravity.
Funding
J.B. and A.-K.T. acknowledge financial support from the Göran Gustafsson Foundation for Research in Natural Sciences and Medicine. T.R. and F.L. acknowledge financial support from Wallenberg Wood Science Center (WWSC), Bengt Ingeström's Foundation and ÅForsk (Ångpanneföreningen's Foundation for Research and Development).
Declaration of interest
The authors report no conflict of interest.
Appendix A. QBX parameters
The parameters used are given in table 3. Here, 
$n_\phi$ and 
$n_\theta$ are the number of grid points on the spheroid in the periodic and non-periodic direction, respectively (as explained in § 3.2); 
$r/h$ controls the distance from each expansion centre to the particle surface (
$h=2{\rm \pi} l r_{p}^{-1}/n_\phi$); 
$\kappa$ is the upsampling factor of the grid; 
$p$ denotes the order of the expansions. The Matlab functions gmres and ode113 are used for solving systems of linear equations and ordinary differential equations, respectively. For a more detailed explanation of these parameters, we refer to af Klinteberg & Tornberg (Reference af Klinteberg and Tornberg2016).
Table 3. Parameters used for the QBX method.
Appendix B. Derivation of the force in a parabolic velocity profile
Chwang (Reference Chwang1975) uses a paraboloidal flow 
$\boldsymbol {u}_{bg}^{Chw}(\boldsymbol {x}) = (1/2) (x_2^2+x_3^2) \boldsymbol {e}_1$, which leads to the force 
$\boldsymbol {F}^{Chw} = \boldsymbol {F}_0 + \boldsymbol {F}^{par}_{Chw}$, where 
$\boldsymbol {F}_0$ is as in (5.6) and
\begin{align} \boldsymbol{F}^{par}_{Chw}(\phi, \boldsymbol{x}_{CM}) &= \frac{8 {\rm \pi}E^3 \cos\phi}{3} \frac{3x_{{CM},2}^2 + {2-E^2} - E^2 \cos^2\phi}{-2E + (1+E^2) \log[(1+E)/(1-E)]} \boldsymbol{e}'_1 \nonumber\\ & \quad - \frac{16 {\rm \pi}E^3 \sin\phi}{3} \frac{3x_{{CM},2}^2 + {2-E^2} - E^2 \cos^2\phi}{2E + (3E^2 - 1) \log[(1+E)/(1-E)]} \boldsymbol{e}'_2. \end{align}
By adjusting the derivation by Chwang (Reference Chwang1975) to the parabolic flow 
$\boldsymbol {u}_{bg}(\boldsymbol {x}) = (1/2) x_2^2 \boldsymbol {e}_1$ used in this paper, we find that the force is 
$\boldsymbol {F} = \boldsymbol {F}_0 + \boldsymbol {F}^{par}$ as in § 5.1.2. The torque on the particle is unaffected by the quadratic terms and is thus the same in the parabolic flow 
$\boldsymbol {u}_{bg}(\boldsymbol {x})$ and the paraboloidal flow 
$\boldsymbol {u}_{bg}^{Chw}(\boldsymbol {x})$, given by (5.3) in both cases.
Chwang (Reference Chwang1975) found that a particle with 
${St}_{trans.}=0$ moving in the paraboloidal flow 
$\boldsymbol {u}_{bg}^{Chw}(\boldsymbol {x})$ will have the velocity
\begin{equation} \boldsymbol{V}^{Chw}(\phi,\boldsymbol{x}_{CM}) = \tfrac{1}{6} ( 3x_{{CM},2}^2 + {2-E^2} - E^2\cos^2\phi ) \boldsymbol{e}_1. \end{equation}
In the parabolic flow 
$\boldsymbol {u}_{bg}{\boldsymbol {x}}$ the velocity 
$\boldsymbol {V}$ is instead given by (5.10). Note that the difference
\begin{equation} \boldsymbol{V}^{Chw} - \boldsymbol{V} = \tfrac{1}{6} (1-E^2) \boldsymbol{e}_1, \end{equation}
is independent of 
$\phi$ and 
$\boldsymbol {x}_{CM}$.
Open access
