Let
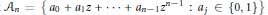 ${{A}_{n}}\,=\,\{{{a}_{0}}+{{a}_{1}}z+\,.\,.\,.\,+\,{{a}_{n-1}}{{z}^{n-1}}\,:\,{{a}_{j}}\,\in \,\{0,1\}\}$
, whose elements are called zero-one polynomials and correspond naturally to the
${{A}_{n}}\,=\,\{{{a}_{0}}+{{a}_{1}}z+\,.\,.\,.\,+\,{{a}_{n-1}}{{z}^{n-1}}\,:\,{{a}_{j}}\,\in \,\{0,1\}\}$
, whose elements are called zero-one polynomials and correspond naturally to the
 ${{2}^{n}}$
subsets of
${{2}^{n}}$
subsets of  $\left[ n \right]\,:=\,\{0,\,1,\,.\,.\,.\,,\,n-1\}$. We also let
$\left[ n \right]\,:=\,\{0,\,1,\,.\,.\,.\,,\,n-1\}$. We also let
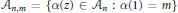 ${{A}_{n,m\,}}\,=\,\{\alpha \left( z \right)\,\in \,{{A}_{n}}\,:\,\alpha \left( 1 \right)\,=\,m\}$
, whose elements correspond to the
${{A}_{n,m\,}}\,=\,\{\alpha \left( z \right)\,\in \,{{A}_{n}}\,:\,\alpha \left( 1 \right)\,=\,m\}$
, whose elements correspond to the
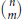 $\left( _{m}^{n} \right)$
subsets of
$\left( _{m}^{n} \right)$
subsets of  $\left[ n \right]$ of size
$\left[ n \right]$ of size 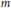 $m$, and let
$m$, and let
 ${{B}_{n}}\,=\,{{A}_{n+1}}\,\backslash \,{{A}_{n}}$
, whose elements are the zero-one polynomials of degree exactly
${{B}_{n}}\,=\,{{A}_{n+1}}\,\backslash \,{{A}_{n}}$
, whose elements are the zero-one polynomials of degree exactly  $n$.
$n$.
Many researchers have studied norms of polynomials with restricted coefficients. Using
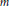 $\|\alpha {{\|}_{p}}$
to denote the usual
$\|\alpha {{\|}_{p}}$
to denote the usual
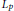 ${{L}_{p}}$
norm of
${{L}_{p}}$
norm of  $\alpha$ on the unit circle, one easily sees that
$\alpha$ on the unit circle, one easily sees that
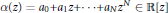 $\alpha \left( z \right)\,=\,{{a}_{0}}+{{a}_{1}}z+.\,.\,.+{{a}_{N}}{{z}^{N}}\,\in \,\mathbb{R}\left[ z \right]$
satisfies
$\alpha \left( z \right)\,=\,{{a}_{0}}+{{a}_{1}}z+.\,.\,.+{{a}_{N}}{{z}^{N}}\,\in \,\mathbb{R}\left[ z \right]$
satisfies
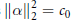 $\|\alpha \|_{2}^{2}\,=\,{{c}_{0}}$
and
$\|\alpha \|_{2}^{2}\,=\,{{c}_{0}}$
and
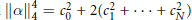 $\|\alpha \|_{4}^{4}\,=\,c_{0}^{2}\,+\,2\left( c_{1}^{2}\,+\,.\,.\,.\,+\,c_{N}^{2} \right)$
, where
$\|\alpha \|_{4}^{4}\,=\,c_{0}^{2}\,+\,2\left( c_{1}^{2}\,+\,.\,.\,.\,+\,c_{N}^{2} \right)$
, where
 ${{c}_{k}}\,:=\,\sum _{j=0}^{N-k}\,{{a}_{j}}{{a}_{j+k}}\,\text{for}\,\text{0}\le \,\text{k}\,\le N$.
${{c}_{k}}\,:=\,\sum _{j=0}^{N-k}\,{{a}_{j}}{{a}_{j+k}}\,\text{for}\,\text{0}\le \,\text{k}\,\le N$.
If
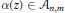 $\alpha \left( z \right)\,\in \,{{A}_{n,m}}$
, say
$\alpha \left( z \right)\,\in \,{{A}_{n,m}}$
, say
 $\alpha \left( z \right)\,=\,{{z}^{{{\text{ }\!\!\beta\!\!\text{ }}_{1}}}}\,+\,.\,.\,.\,+\,{{z}^{{{\text{ }\!\!\beta\!\!\text{ }}_{m}}}}$ where
$\alpha \left( z \right)\,=\,{{z}^{{{\text{ }\!\!\beta\!\!\text{ }}_{1}}}}\,+\,.\,.\,.\,+\,{{z}^{{{\text{ }\!\!\beta\!\!\text{ }}_{m}}}}$ where 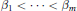 ${{\beta }_{1}}\,<\,.\,.\,.\,<\,{{\beta }_{m}}$
, then
${{\beta }_{1}}\,<\,.\,.\,.\,<\,{{\beta }_{m}}$
, then
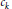 ${{c}_{k}}$
is the number of times
${{c}_{k}}$
is the number of times  $k$ appears as a difference
$k$ appears as a difference
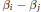 ${{\beta }_{i}}\,-\,{{\beta }_{j}}$
. The condition that
${{\beta }_{i}}\,-\,{{\beta }_{j}}$
. The condition that
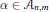 $\alpha \,\in \,{{A}_{n,m}}$
satisfies
$\alpha \,\in \,{{A}_{n,m}}$
satisfies
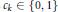 ${{c}_{k}}\,\in \,\{0,1\}$
for
${{c}_{k}}\,\in \,\{0,1\}$
for 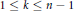 $1\,\le \,k\,\le \,n\,-\,1$ is thus equivalent to the condition that
$1\,\le \,k\,\le \,n\,-\,1$ is thus equivalent to the condition that
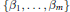 $\{{{\beta }_{1}},\,.\,.\,.\,,\,{{\beta }_{m}}\}$
is a Sidon set (meaning all differences of pairs of elements are distinct).
$\{{{\beta }_{1}},\,.\,.\,.\,,\,{{\beta }_{m}}\}$
is a Sidon set (meaning all differences of pairs of elements are distinct).
In this paper, we find the average of
 $\left\| \alpha \right\|_{4}^{4}$
over
$\left\| \alpha \right\|_{4}^{4}$
over
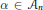 $\alpha \,\in \,{{A}_{n}}$,
$\alpha \,\in \,{{A}_{n}}$, 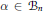 $\alpha \,\in \,{{B}_{n}}$ and
$\alpha \,\in \,{{B}_{n}}$ and  $\alpha \,\in \,{{A}_{n,m}}$. We further show that our expression for the average of
$\alpha \,\in \,{{A}_{n,m}}$. We further show that our expression for the average of
 $\left\| \alpha \right\|_{4}^{4}$
over
$\left\| \alpha \right\|_{4}^{4}$
over
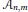 ${{A}_{n,m}}$
yields a new proof of the known result: if
${{A}_{n,m}}$
yields a new proof of the known result: if
 $m\,=\,o\left( {{n}^{1/4}} \right)$
and
$m\,=\,o\left( {{n}^{1/4}} \right)$
and 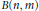 $B\left( n,\,m \right)$ denotes the number of Sidon sets of size
$B\left( n,\,m \right)$ denotes the number of Sidon sets of size 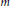 $m$ in
$m$ in  $\left[ n \right]$, then almost all subsets of
$\left[ n \right]$, then almost all subsets of  $\left[ n \right]$ of size
$\left[ n \right]$ of size 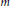 $m$ are Sidon, in the sense that
$m$ are Sidon, in the sense that
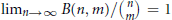 ${{\lim }_{n\to \infty }}\,B\left( n,\,m \right)/\left( _{m}^{n} \right)\,=\,1$.
${{\lim }_{n\to \infty }}\,B\left( n,\,m \right)/\left( _{m}^{n} \right)\,=\,1$.