Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T18:45:11.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal Inner Functions on the Ball

Published online by Cambridge University Press:  20 November 2018

Frédéric Bayart
Frédéric Bayart*
Affiliation:
Laboratoire Bordelais d’Analyse et de Géométrie, UMR 5467, Université Bordeaux 1, 33405 Talence Cedex, France. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that given any sequence of automorphisms 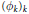${{\left( {{\phi }_{k}} \right)}_{k}}$ of the unit ball 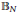${{\mathbb{B}}_{N}}$ of 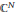${{\mathbb{C}}^{N}}$ such that 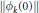$\left\| {{\phi }_{k}}\left( 0 \right) \right\|$ tends to 1, there exists an inner function $I$ such that the family of “non-Euclidean translates” 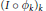${{\left( I\,\text{o}\,{{\phi }_{k}} \right)}_{k}}$ is locally uniformly dense in the unit ball of 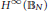${{H}^{\infty }}\left( {{\mathbb{B}}_{N}} \right)$ .

Keywords

32A3530D5047B38inner functionsautomorphisms of the balluniversality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 4 , 01 December 2008 , pp. 481 - 486
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Alexandrov, A. B., Function theory in the ball. In: Several Complex Variables. II, Encyclopaedia of Mathematical Sciences, Springer-Verlag, Berlin, 1994.Google Scholar
[2] Bayart, F., Universal radial limits of holomorphic functions. Glasg Math. J. 47(2005), no. 2, 261–267.Google Scholar
[3] Chee, P. S., Universal functions in several complex variables. J. Austral. Math. Soc. A28(1979), no. 2, 189–196.Google Scholar
[4] Gauthier, P. M. and Xiao, J., The existence of universal inner functions on the unit ball of ℂ N . Canad. Math. Bull. 48(2005), no. 3, 409–413.Google Scholar
[5] Gorkin, P. and Mortini, R., Universal Blaschke products. Math. Proc. Cambridge Philos. Soc. 136(2004), no. 1, 175–184.Google Scholar
[6] Heins, M., A universal Blaschke product. Archiv Math. 6(1954), 41–44.Google Scholar
[7] Nestoridis, V., Universal Taylor series. Ann. Inst. Fourier (Grenoble) 46(1996), no. 5, 1293–1306.Google Scholar
[8] Rudin, W., Function Theory in the Unit Ball of ℂ N. Grundlehren der Mathematischen Wissenschaften 241, Springer-Verlag, New York, 1980.Google Scholar