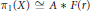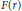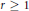Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Khan, Qayum
2012.
Homotopy invariance of 4-manifold decompositions: Connected sums.
Topology and its Applications,
Vol. 159,
Issue. 16,
p.
3432.