Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-11T05:05:58.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Summation of Series over Bourget Functions

Published online by Cambridge University Press:  20 November 2018

Mirjana V. Vidanović ,
Slobodan B. Tričković  and
Miomir S. Stanković
Mirjana V. Vidanović
Affiliation:
Department of Mathematics, Faculty of Environmental Engineering, University of Niš, 18000 Niš, Serbia. e-mail: [email protected]@znrfak.ni.ac.yu
Slobodan B. Tričković
Affiliation:
Department of Mathematics, Faculty of Civil Engineering, University of Niš, 18000 Niš, Serbia. e-mail: [email protected]
Miomir S. Stanković
Affiliation:
Department of Mathematics, Faculty of Environmental Engineering, University of Niš, 18000 Niš, Serbia. e-mail: [email protected]@znrfak.ni.ac.yu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we derive formulas for summation of series involving J. Bourget's generalization of Bessel functions of integer order, as well as the analogous generalizations by H. M. Srivastava. These series are expressed in terms of the Riemann 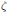$\zeta$ function and Dirichlet functions 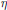$\eta$, 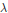$\lambda$, 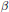$\beta$, and can be brought into closed form in certain cases, which means that the infinite series are represented by finite sums.

Keywords

33C1011M0665B10Riemann zeta functionBessel functionBourget functionDirichlet function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 4 , 01 December 2008 , pp. 627 - 636
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Abramowitz, M. and Stegun, A., eds., Handbook ofMathematical Functions, with Formulas, Graphs and Mathematical Tables. Dover, New York, 1972.Google Scholar
[2] Bourget, J., Mémoire sur les nombres de Cauchy et leur application à divers problèmes de mécanique céleste. J. de Math.(2) 6(1861), 33–54.Google Scholar
[3] Gorowara, K. K., On Bourget's function Jn,k(z). Ganita 22(1971), no. 1, 21–26.Google Scholar
[4] Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals, Series and Products. Sixth edition. Academic Press, San Diego, CA, 2000.Google Scholar
[5] Prudnikov, A. P., Brychkov, Y. A., and Marichev, O. I., Integrals and Series, Volume 1, Elementary Functions. Gordon and Breach Science Publishers, New York, 1986.Google Scholar
[6] Srivastava, H. M., A note on functions analogous to Bourget's function. Ganita 19(1968), no. 2, 45–48.Google Scholar
[7] Stanković, M. S., Vidanović, M. V., and Tričković, S. B., On the summation of series involving Bessel or Struve functions. J. Math. Anal. Appl. 247(2000), no. 1, 15–26.Google Scholar
[8] Tričković, S. B., Vidanović, M. V., and Stanković, M. S., On the summation of series in terms of Bessel functions. Z. Anal. Anwend. 25(2006), no. 3, 393–406.Google Scholar
[9] Tričković, S. B., Vidanović, M. V., and Stanković, M. S. On the summation of trigonometric series. Integral Transforms Spec. Funct. 19(2008), no. 6, 441–452.Google Scholar
[10] Watson, G. N., A Treatise on the Theory of Bessel Functions. Second edition. Cambridge University Press, Cambridge, 1944.Google Scholar