1. Let (xn, Xn) denote a basis for a Banach space (X, ∥ • ∥) of measurable functions in (0, 1).
It is shown in [2] and [9] that the equivalence of the norms
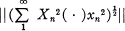
and ∥ • ∥ is equivalent to the unconditionality of the basis (xn, Xn). In [8] a weaker relationship between these norms is exploited to establish the existence of an element of L1(E) for each E ⊂ (0, 1), |£| > 0, whose Haar series expansion is conditionally convergent in the norm of L\(E).
In this note, a Lemma of Orlicz [7] is generalized to provide a relationship between 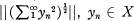 , and the changes in sign that are tolerated in
, and the changes in sign that are tolerated in 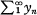 without disruption of norm convergence.
without disruption of norm convergence.

 a covering of
a covering of 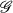 of
of 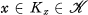 and an open set
and an open set  such that
such that 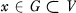 . In such a case
. In such a case 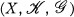 .
.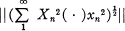
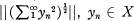 , and the changes in sign that are tolerated in
, and the changes in sign that are tolerated in 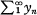 without disruption of norm convergence.
without disruption of norm convergence.