Research Article
A class of majorant functions for contractors and equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 51-58
-
- Article
-
- You have access
- Export citation
Matrix quadratic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-401
-
- Article
-
- You have access
- Export citation
Jackson's Theorem for locally compact abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 59-66
-
- Article
-
- You have access
- Export citation
Padé approximation and orthogonal polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-270
-
- Article
-
- You have access
- Export citation
Entire functions mapping countable dense subsets of the reals onto each other monotonically
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-70
-
- Article
-
- You have access
- Export citation
Submartingales and stochastic stability
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-276
-
- Article
-
- You have access
- Export citation
Ascoli theorems and the pseudocharacter of mapping spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 403-408
-
- Article
-
- You have access
- Export citation
Recurrent tensors and holonomy group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-77
-
- Article
-
- You have access
- Export citation
Some remarks on coherent soluble groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 277-279
-
- Article
-
- You have access
- Export citation
Commutative Banach algebras with non-unique complete norm topology
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 409-420
-
- Article
-
- You have access
- Export citation
A new definition of discrete analytic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 281-291
-
- Article
-
- You have access
- Export citation
On the edge-reconstruction of graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-84
-
- Article
-
- You have access
- Export citation
Path decompositions of digraphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-427
-
- Article
-
- You have access
- Export citation
Diffraction of planetary waves by an infinite strip
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-304
-
- Article
-
- You have access
- Export citation
Two-variable laws for a class of finite simple groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 85-89
-
- Article
-
- You have access
- Export citation
The CREAM conjecture for the subvarieties of certain abelian-by-nilpotent varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-451
-
- Article
-
- You have access
- Export citation
A note on the summation of an infinite series involving a hypergeometric function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-309
-
- Article
-
- You have access
- Export citation
Proof of a conformal mapping relationship
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 91-94
-
- Article
-
- You have access
- Export citation
Nonoscillation of arbitrary order retarded differential equations of non-homogeneous type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 453-458
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Almost periodic generalized functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 311-312
-
- Article
-
- You have access
- Export citation

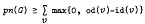 max{0, od(
max{0, od(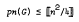 with equality holding if
with equality holding if 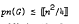 for any digraph
for any digraph 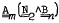 are CREAM in the sense of Higman when
are CREAM in the sense of Higman when