Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-16T01:18:33.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Path decompositions of digraphs

Published online by Cambridge University Press:  17 April 2009

Brian R. Alspach  and
Norman J. Pullman
Brian R. Alspach
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, British Columbia, Canada
Norman J. Pullman
Affiliation:
Department of Mathematics, Queen's University, Kingston, Ontario, Canada.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A path decomposition of a digraph G (having no loops or multiple arcs) is a family of simple paths such that every arc of G lies on precisely one of the paths of the family. The path number, pn(G) is the minimal number of paths necessary to form a path decomposition of G.

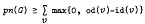We show that pn(G) ≥ max{0, od(v)-id(v)} the sum taken over all vertices v of G, with equality holding if G is acyclic. If G is a subgraph of a tournament on n vertices we show that pn(G) ≤ 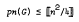with equality holding if G is transitive.

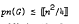We conjecture that pn(G) ≤ for any digraph G on n vertices if n is sufficiently large, perhaps for all n ≥ 4.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 10 , Issue 3 , June 1974 , pp. 421 - 427
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Erdös, P., “Some unsolved problems in graph theory and combinatorial analysis”, Combinatorial mathematics and its applications, 97–109 (Proc. Conf. Math. Institute, Oxford, Jul, 1969. Academic Press, London and New York, 1971).Google Scholar
[2]Harary, Frank, Schwenk, Allen J., “Evolution of the path number of a graph: covering and packing in graphs, II”, Graph theory and computing, 39–45 (Academic Press, New York and London, 1972).CrossRefGoogle Scholar
[3]Lovasz, L., “On covering of graphs”, Theory of graphs, 231–236 (Proc. Colloq. Tihany, Hungary, 09, 1966. Academic Press, New York and London, 1968).Google Scholar
[4]Stanton, R.G., Cowan, D.D., James, L.O., “Some results on path numbers”, Proceedings of the Louisiana Conference on Combinatorics, Graph Theory and Computing (1970), 112–135 (Louisana State University, Baton Rouge, 1970).Google Scholar