Large variations in values of the diffusion coefficient for snow have been reported in the literature. Some authors (Yosida and others, 1955; Yen, 1963) have claimed that the diffusion coefficient does not vary with density. Others (Colbeck, 1993; Arons and Colbeck, 1995) have reported that the diffusion coefficient decreases with an increase in mean pore length, and that it does not necessarily change with snow density. This appears to be inconsistent, since density and mean pore space are related for a given mass of snow and therefore these parameters cannot be taken independently. On the other hand, experimental results show an increase in grain-growth rate with decrease in snow density. In this paper, particulate and continuum approaches have been used to obtain the mass diffusivity Treating snow as a particulate medium, the one-dimensional model of grain growth from Satyawali (1994) has been extended. This approach has been integrated into the SNOWPACK model (Lehning and others, 1998) that predicts the rate of grain growth for a dry snowpack subject to a temperature gradient. The expression for effective vapor-diffusion coefficient resulting from the present study is
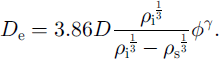
To test this equation, several experiments similar to those of Yosida and others (1955) have been conducted assuming that snow is a continuous medium. In this approach Fick’s law of diffusion is used to obtain direct experimental determinations of the diffusion coefficient. The experimental results have been compared to estimates of D∊ calculated from the above equation and it is shown that results are inconsistent at the upper and lower sample boundaries. This paper describes the features of snow metamorphism, in particular grain growth driven by an applied temperature gradient, and discusses the mass-diffusivity coefficient derived from the particle theory of Colbeck (1993).