Introduction

Preferential deposition of snow and redistribution of already deposited snow are both governed by the interaction between topography, vegetation and wind, and play an extremely important role in the build-up of the seasonal snow cover in alpine terrain. Their influence on avalanche activity cannot be overestimated, and avalanche forecasters have long been asking for an operational assessment of snowdrift.

Because of its importance, snowdrift has been studied intensively. Most of the studies have sought a physical understanding (Reference MellorMellor, 1965; Reference RadokRadok, 1977; Reference Anderson, Sorensen and WillettsAnderson and others, 1991; Reference BintanjaBintanja, 1998; Reference GauerGauer, 1998). It is only more recently that attempts have been undertaken to combine physical principles with experimental results (Reference MeisterMeister, 1989; Reference CastelleCastelle, 1995; Reference McKenna Neuman and MaljaarsMcKenna Neuman and Maljaars, 1997) to build model descriptions of snowdrift (Reference Liston, Brown and DentListon and others, 1993; Reference Pomeroy, Gray and LandinePomeroy and others, 1993; Reference GauerGauer, 1998; Reference Listen and SturmListon and Sturm, 1998). Only one prototype wind-drift model, which includes a detailed analysis of the snow cover (Reference Brun, David, Sudul and BrunotBrun and others, 1992), has so far been used for avalanche forecasting (Reference Guyomarc’h and MerindolGuyomarc’h and Merindol, 1998).

The new SNOWPACK model developed at the Swiss Federal Institute for Snow and Avalanche Research (Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others, 1999) is a one-dimensional momentum, mass- and energy-balance model. Its current version includes important features such as a numerical solution of the instationary heat-transfer and creep/settlement equations, a complete surface-energy balance, phase changes, water transport and snow microstructure development (metamorphism). The microstructural parameters are linked to the thermal conductivity and the snow viscosity. The Lagrangian finite-element solution allows for a realistic representation of the layered snow-cover structure. The model is already in operational use. It calculates the local snow-cover characteristics for approximately 50 automatic Swiss high-Alpine snow and weather stations located 2000–3000 m a.s.l. The measurements of air temperature, humidity, wind, snow-surface temperature, reflected shortwave radiation, ground temperature and snow height are used as boundary conditions for the model. Of special importance is the snow height, which is used to determine the amount of new snow (Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others, 1999). Although the stations have been selected for negligible snowdrift influence, some stations show significant snowdrift influence for certain wind directions. We demonstrate that a simple model of snowdrift applied to the SNOWPACK model calculations and driven by the meteorological input data from the automatic stations yields reliable estimates of local snowdrift and improves the seasonal snow-cover simulation considerably. The magnitude of local snowdrift as estimated by the model is operationally available to the Swiss national avalanche warning service and local avalanche experts.

Model Formulation

The drift routine is an integral part of the SNOWPACK model. The finite-element structure of the model (Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others, 1999) is ideal for modelling erosion and deposition of snow layers. The model first determines a threshold wind speed for erosion of the focal snowpack dependent on our microstructural parameters: grain-size, bond size, coordination number and sphericity of the uppermost snow element. In the absence of better knowledge, we assume a logarithmic wind profile. Starting with an estimate based on our own measurements for the roughness length, z₀ (m), depending on the grain-size, r_g (m),

we solve iteratively for the friction velocity, u* (m s^–1), and z₀:

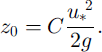
Here the model grain radius, r_g, the measured wind speed, ω (ms–1 at height z (m) above the ground and the von Kármán constant, k (0.4), are used. This formulation of the roughness length (Reference OwenOwen, 1964) takes into account that the roughness length increases in the presence of snowdrift and is proportional to the height of the saltation layer. The parameter C is set to 0.12 (Reference Listen and SturmListon and Sturm, 1998). We follow Reference SchmidtSchmidt (1980) for the formulation of the threshold friction velocity,_u*t(ms^ȡ1):

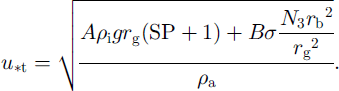
All his geometrical expressions have been included in the parameters A (0.018) and B (0.0135). SP ([0;1]) is the model sphericity, N₃ is the model coordination number, τ_b is the model bond radius, a is a reference shear strength set to 300 Pa and _A and ρ_a (kg m^–3) are the densities of ice and air, respectively. From the threshold friction velocity we can determine a threshold wind velocity using Equation (2) and compare the threshold wind speed to the measured wind speed. The wind-speed sensor at the Interkantonales Mess- und Informations system (IMIS) stations (Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others, 1999) is approximately 7.5 m above ground, and for the comparison we take into account the actual depth of the snow cover. If the measured wind speed is below the threshold, no erosion of already deposited snow is assumed. If the wind speed indicates erosion, we calculate a mass flux or transport rate. We distinguish between two transport modes: saltation of snow particles and transport in suspension (Reference GauerGauer, 1998). For the mass flux in saltation, Q_salt (kg m–1 s^–1), the parameterization of Reference Pomeroy and GrayPomeroy and Gray (1990) is adapted:

The mass flux in suspension, Q_susp (kg m–1 s^–1), results from the integration:

The reference height, z_ref(m) (m), is the height of the saltation layer and is proportional to the roughness length. Thus, it can be parameterized using Equation (3) with the constant, C, set to 1.6 (Reference Greeley and IversenGreeley and Iversen, 1985). From the one-dimensional diffusion equation, we obtain the snow-particle mass-concentration profile, c(z) (kg m^–3):

A settling velocity, s, of 0.3 m s–1 is assumed. The concentration at the height of the saltation layer, c(z_ref), is parameterized by (Liston and Sturm, 1998):

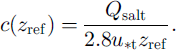
The implementation in SNOWPACK is such that for each time-step the erodibility of the uppermost layer is checked and if the snow-dependent threshold wind speed is reached, the layer is eroded and the total mass flux according to Equations (5) and (6) is calculated. The same procedure is then applied to the next layer until a layer is reached which cannot be eroded under the current weather and snow conditions. From the mass flux, we construct a semi-quantitative drift index by averaging all the mass fluxes for the past 24 or 6 hours.Footnote * This index is calculated for all IMIS stations and is available in real time to our national avalanche forecasting group and to about 200 local forecasters/committees.

The current operational implementation does not yet take into account the drift contribution from snow precipitation, because we have no direct measurement of precipitation at the IMIS stations. The precipitation rates are estimated from the difference between measured and modelled snow heights under the assumption of no drift influence (Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others, 1999). This estimation becomes obsolete for the stations where we observe snowdrift and use the drift model to describe possible erosion of the snow cover.

For winter 1999/2000 it is planned to have an independent estimation of precipitation for all stations, based on a three-dimensional kriging interpolation of available measurements at the automatic stations from the meteorological institute and a meteorological model analysis. Also note that because of the new snow-estimation procedure, possible deposition of snow at some stations due to wind drift cannot be distinguished from snowfall. However, the drift index should also indicate this mass flux as long as the threshold friction velocity is reached.

Results

We present seasonal snow-cover simulations for two IMIS station: Klosters and Simplon. Klosters shows no significant snowdrift influence, while Simplon is heavily influenced by erosion of the snow cover. Figure 1 shows a comparison between measured and modelled snow depths for Klosters when the snowdrift erosion mechanism is switched off. The settling rates are well predicted by the model, and the two curves show a very good agreement using the settling laws and new snow treatment described in Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others (1999). By contrast, Figure 2a shows a great difference between measured and modelled snow depths at Simplon where erosion of the snow cover is not taken into account. The result with the snowdrift routine switched on is presented in Figure 2b. A considerable improvement in the modelled snow depth is visible. There are still periods when erosion is underestimated by the model (e.g. after 27 October) or when the model erodes too much snow (e.g. after 25 February). However, we want to emphasize that most of the drift events are well represented by our simple drift formulation. The problem of exaggerated erosion can and must be fixed for the operational application. For this purpose, we simply require the modelled snow depth to be greater than the measured one in order to allow erosion. Figure 3 focuses on the intense avalanche period of January-February 1999 and shows the comparison between simulation without snowdrift (Fig. 3a) and simulation with snowdrift, including the application of the erosion-limitation criterion (Fig. 3b). The limited-erosion check ensures that the seasonal snow-cover simulation is consistent. In case of overestimated erosion, the new snow routines would add new snow to the simulation as soon as the snowfall conditions are fulfilled. An erroneous build-up of the seasonal snow cover would result. A further advantage of this erosion check is that in case of snow deposition at the station the drift index will react properly and show mass transport as long as the friction velocity is reached, because the new snow layers (which have small threshold friction velocities according to Equation (4)) will not be eroded.

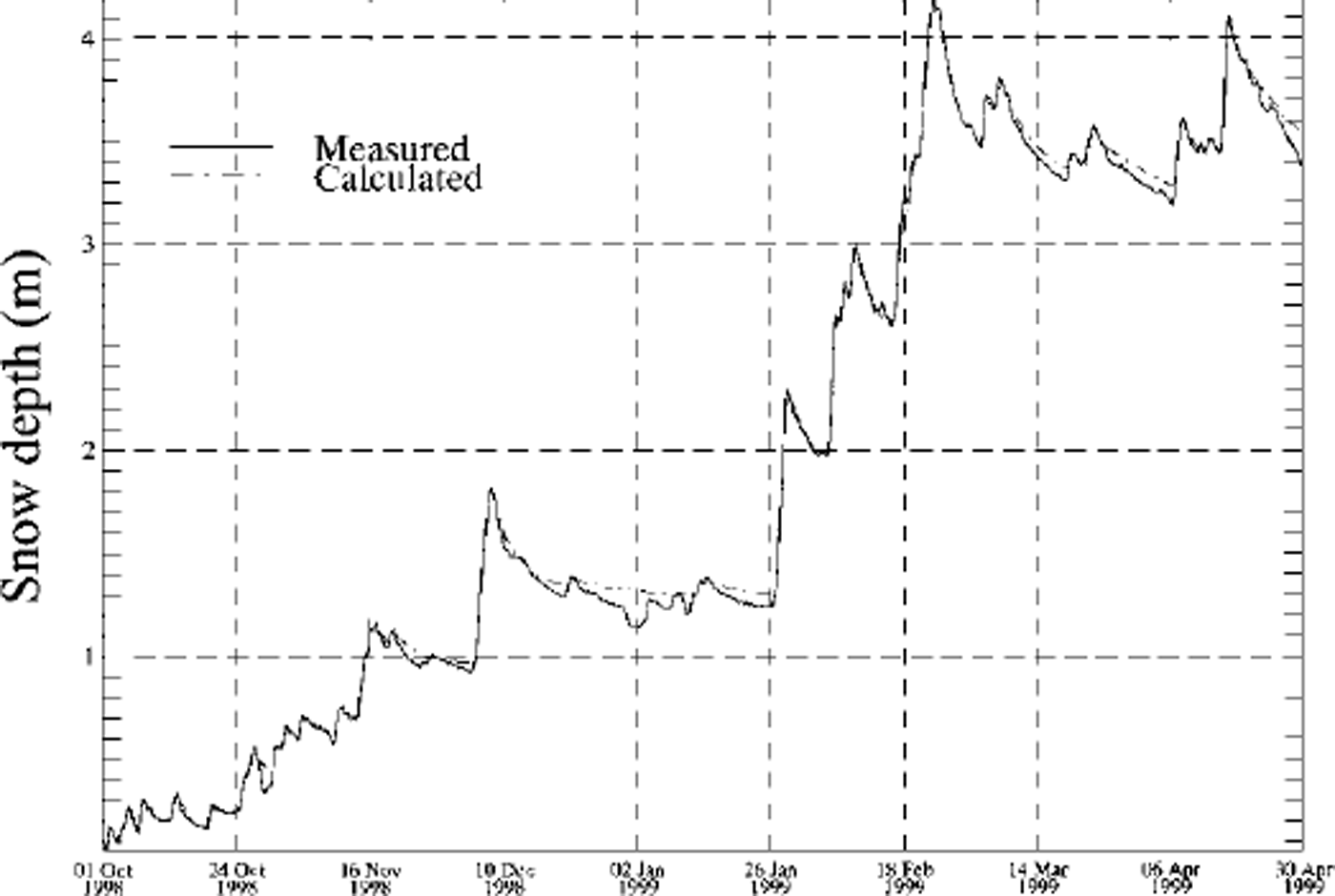
Fig. 1. Comparison between measured and modelled snow depth for the station Klosters. The model is run without the snowdrift routine. The station shows negligible snowdrift influence. Due to measurement errors, the measured curve is always less smooth than the model curve.

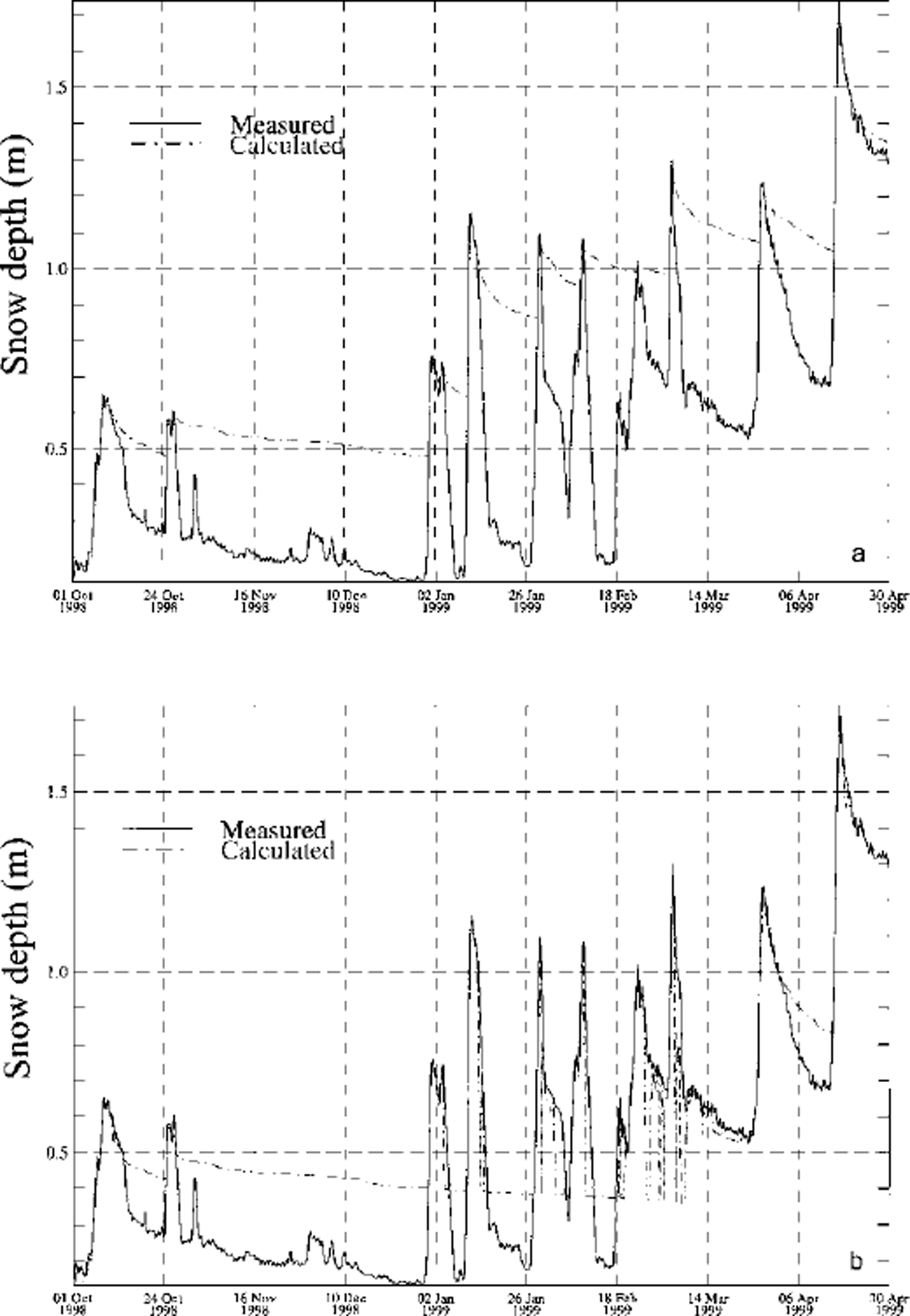
Fig. 2. (a) The station Simplon shows a significant snowdrift influence resulting in considerable disagreement between modelled and measured snow depth when snowdrift is not taken into account, (b) The snowdrift routine improves the simulation.

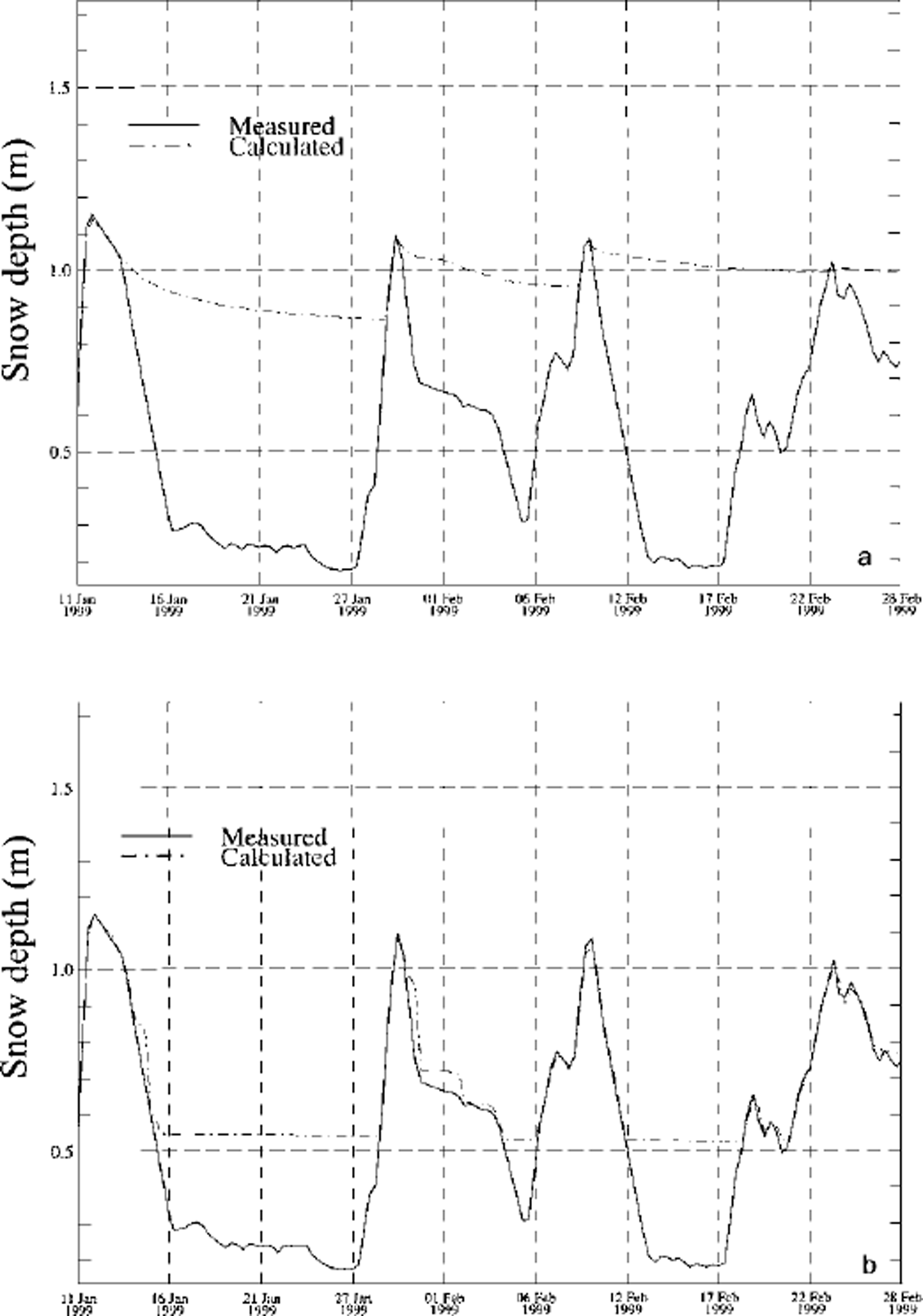
Fig. 3. During the period of high avalanche activity in January-February 1999, four large snowfall events were observed at Simplon. The new snow had regularly been eroded following the snowfall events (a) in the model without snowdrift. Using the limitation of possible erosion by the measured snow height, a more realistic representation of the seasonal snow-cover development results (b) with the snowdrift model.

The formulation of the grain-wind interaction can be improved. The reason for the underestimation of erosion as seen in Figure 3b is found by inspecting the modelled grain type of the layer where the erosion stops (Fig. 4). The layer of depth hoar which had previously been subjected to marginal melting (Ao) cannot be eroded. Figure 2b shows that this is the layer which the model failed to erode after 27 October. The SNOWPACK metamorphism routines tend to overestimate the development rate of faceted crystals and depth hoar (see Reference Lehning, Bartelt, Brown, Russi, Stöckli and ZimmerliLehning and others (1999) for a snow-pit evaluation). This erroneous development already prevented the erosion of the layer following the 27 October drift event (not shown). This demonstrates that a correct description of the seasonal snow-cover development including metamorphism and past drift events is required in order to predict current snowdrift. Despite the limitation of the current formulations, the drift model provides valuable information for the avalanche warning service regarding the drift periods. Figure 5 shows the measured wind speed for the February period (Fig. 5a) and the drift index as obtained from the model (Fig. 5b). All drift periods are associated with high wind speeds, but a high wind speed does not necessarily mean a drift period. Since the avalanche forecaster needs to get a fast overview of the situation for the whole of Switzerland, such an index helps to filter the crucial information from the mass of raw data available.

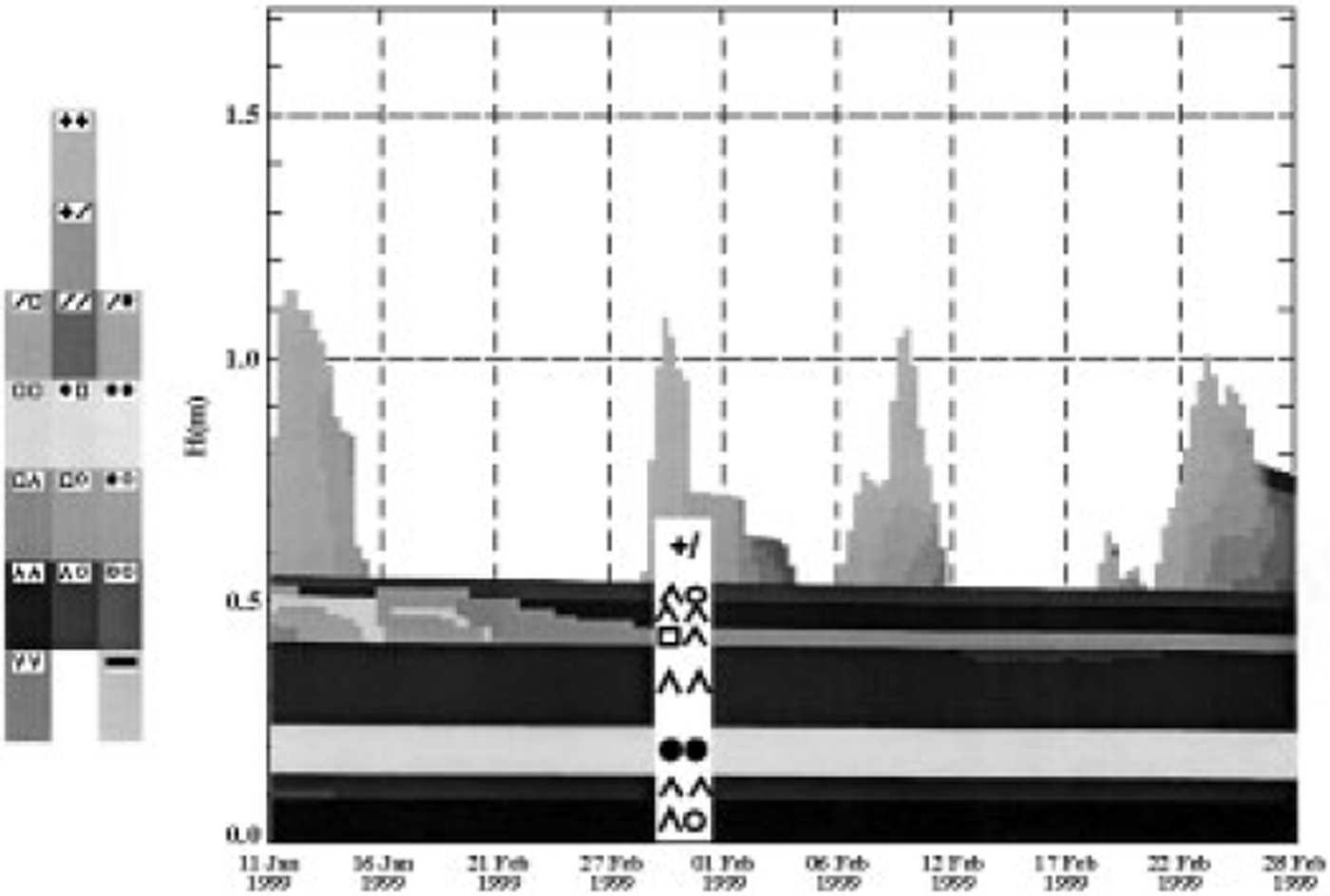
Fig. 4. Simulation of the grain types in SNOWPACK for the high-avalanche-actwity period in 1999 at station Simplon. The modelled layer of depth hoar prevents erosion.

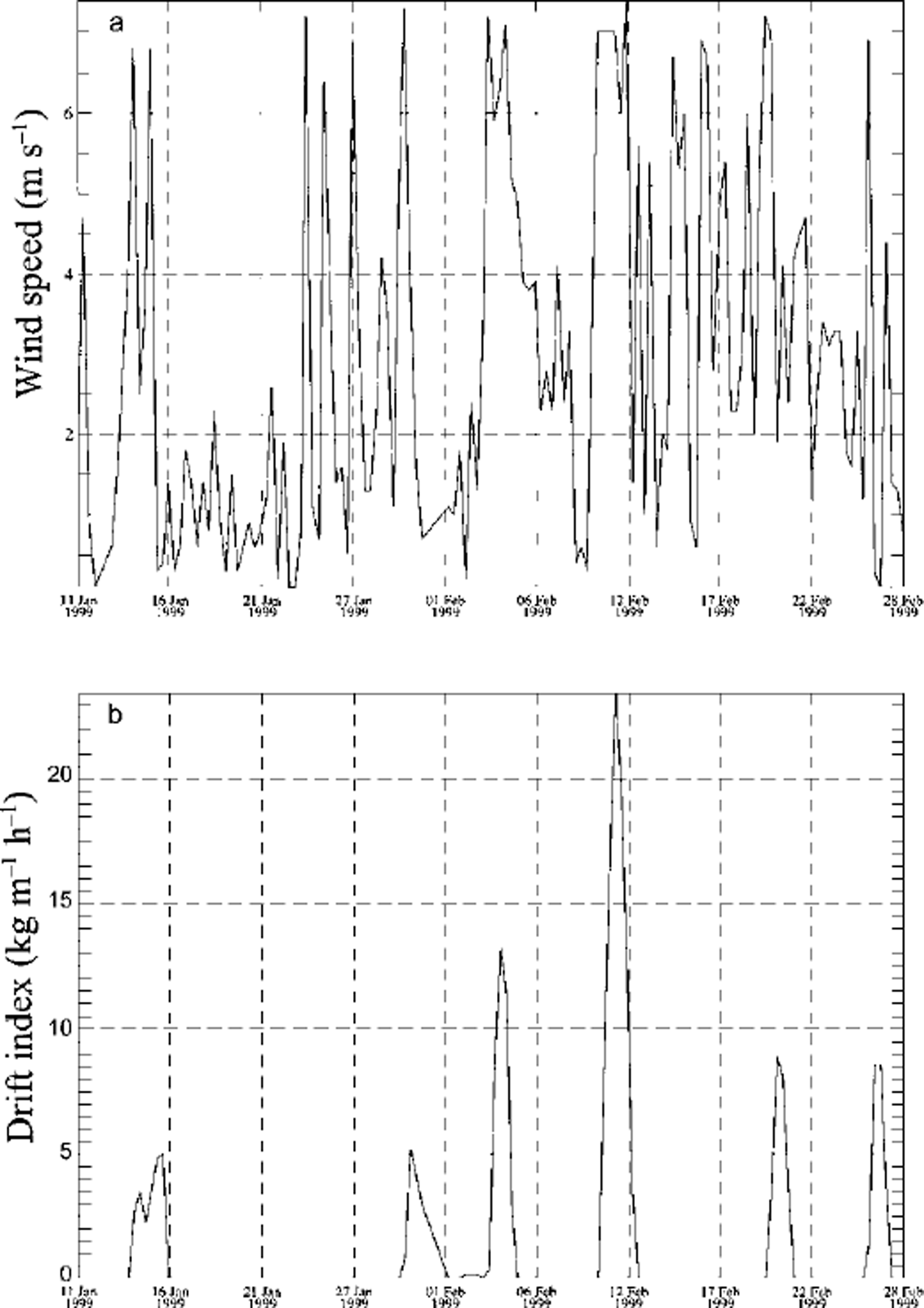
Fig. 5. Measured wind speeds (a) and snowdrift index (b) for station Simplon. The drift index allows ready identification of the occurrence and magnitude of drift periods.

Conclusions, Limitations and Outlook

We presented a snowdrift implementation coupled to the snow-cover model SNOWPACK. The simple snowdrift index as presented has been shown to improve the seasonal snow-cover simulations at IMIS snow stations that show the influence of wind drift. The index based on the calculation of a mass flux is a local indicator for snowdrift and, as such, valuable for the avalanche warning service. The erodibility of the snow cover is assessed by analyzing the microstructural properties as calculated by SNOWPACK. The interaction between the grains and the wind field is based on a physical approach following Reference OwenOwen (1964). The following limitations have to be kept in mind when using the index:

1. (a) The index represents local conditions at the station and is not representative for a larger area.

2. (b) The index in its current implementation does not yet take drift from precipitation into account.

3. (c) The formulation of mass flux is based on equilibrium conditions which might not be reached in the Alpine terrain considered.

4. (d) We assume a logarithmic wind profile which is not influenced by surrounding topography.

We are working to overcome these limitations. Using high-resolution wind-field simulations based on a mesoscale atmospheric prediction model and driven by the operational weather-forecast model output, together with a distributed approach to snow-cover modelling, we aim to estimate snowdrift effects over three-dimensional topography. As already mentioned, an independent estimation of precipitation will soon be available and the current drift index will be improved. Wind-tunnel and field studies will be performed to clarify and improve the drift formulation itself with regard to the interaction between atmospheric turbulence and the snow cover. Finally, the presentation of the control run with unrestricted erosion has shown that the formulation of metamorphism within the snow cover also needs to be improved.