Introduction
Passive microwave sensors are a valuable tool for investigating snow properties because the emission spectra of snowpacks show characteristic signatures. They depend on snow type and snow properties (Reference MatzlerMatzler, 1994). However, to understand the signatures and to quantitatively use them in remote sensing, a physical model is needed. To date, only a few models, often with a limited range of application, have been published. This was the motivation to develop the Microwave Emission Model of Layered Snowpacks (MEMLS; Reference Wiesmann and MatzlerWiesmann and Matzler, 1999; Reference Matzler and WiesmannMatzler and Wiesmann, 1999) which is a multi-polarization, multiple-scattering radiative transfer model, using a six-flux approach to describe volume scattering and absorption, and taking into account trapped radiation due to internal reflection.
One of the major limitations of these models is the necessity to obtain detailed parameters describing the medium. The overall quality of the simulated responses depends on the accuracy of the structural parameters feeding the model, especially when the scattering mechanisms are complex. Up to now, we have used ground measurements to provide input parameters (Reference PulliainenPulliainen and others, 1998; Reference Wiesmann and MatzlerWiesmann and Matzler, 1999). However, these parameters are usually difficult to estimate, especially because of the vertical inhomogeneity of the snowpack (e.g. large number of characteristic layers) and the different approaches used to characterize the snow texture (e.g. grain-size, correlation length).
Here we use snow physical models to provide the input parameters for MEMLS. Such models have been developed to predict the mechanical, thermal and optical properties for various applications, such as climate modeling, avalanche forecasting and hydrology. Recently, snow-cover models were also used for remote-sensing applications (Reference Galantowicz and EnglandGalantowicz and England, 1997; Reference Shih, Ding, Kong and YangShih and others, 1997). In our work we use two different models, namely, SNTHERM.89 and Crocus. SNTHERM, a one-dimensional mass- and energy-balance model of snow physics, was developed at the U. S. Army Cold Regions Research and Engineering Laboratory (CRREL) for predicting temperature profiles within snow and frozen soil (Reference JordanJordan, 1991). The model is formulated to consider a snow cover over soil with high vertical and temporal resolution. Crocus is a one-dimensional numerical energy and mass-evolution model of snow cover, developed by Météo France. Its main objective is operational avalanche forecasting (Reference Brun, Martin, Simon, Gendre and ColéouBrun and others, 1989, Reference Brun, David, Sudul and Brunot1992). Both models use a set of meteorological parameters as input.
The combination of a snow model with the microwave model makes it possible to estimate the microwave emission of a snow-covered terrain from meteorological data. Difficulties arise because snow grains are not clearly delineated on a microscopic scale and cannot be easily quantified in terms of shape and size.
This paper presents the combined forward models (Fig. 1) of the snowpack which first solves for snowpack and soil state (by means of Crocus or SNTHERM, respectively), given external atmospheric forcing, then calculates emissivity by means of MEMLS. The results are compared with measured snow profiles (Reference AmmannAmmann, 1997) and in situ radiometric measurements (Reference Wiesmann, Strozzi and WeiseWiesmann and others, 1996,Reference Wiesmann, Matzler and Weise1998). The results are in reasonable agreement with in situ observations, but discrepancies are found for the polarization difference. The results demonstrate the potential for retrieving snow data from microwave satellite measurements by constraining the snowpack state with local meteorological data through a numercial snow-physical model.
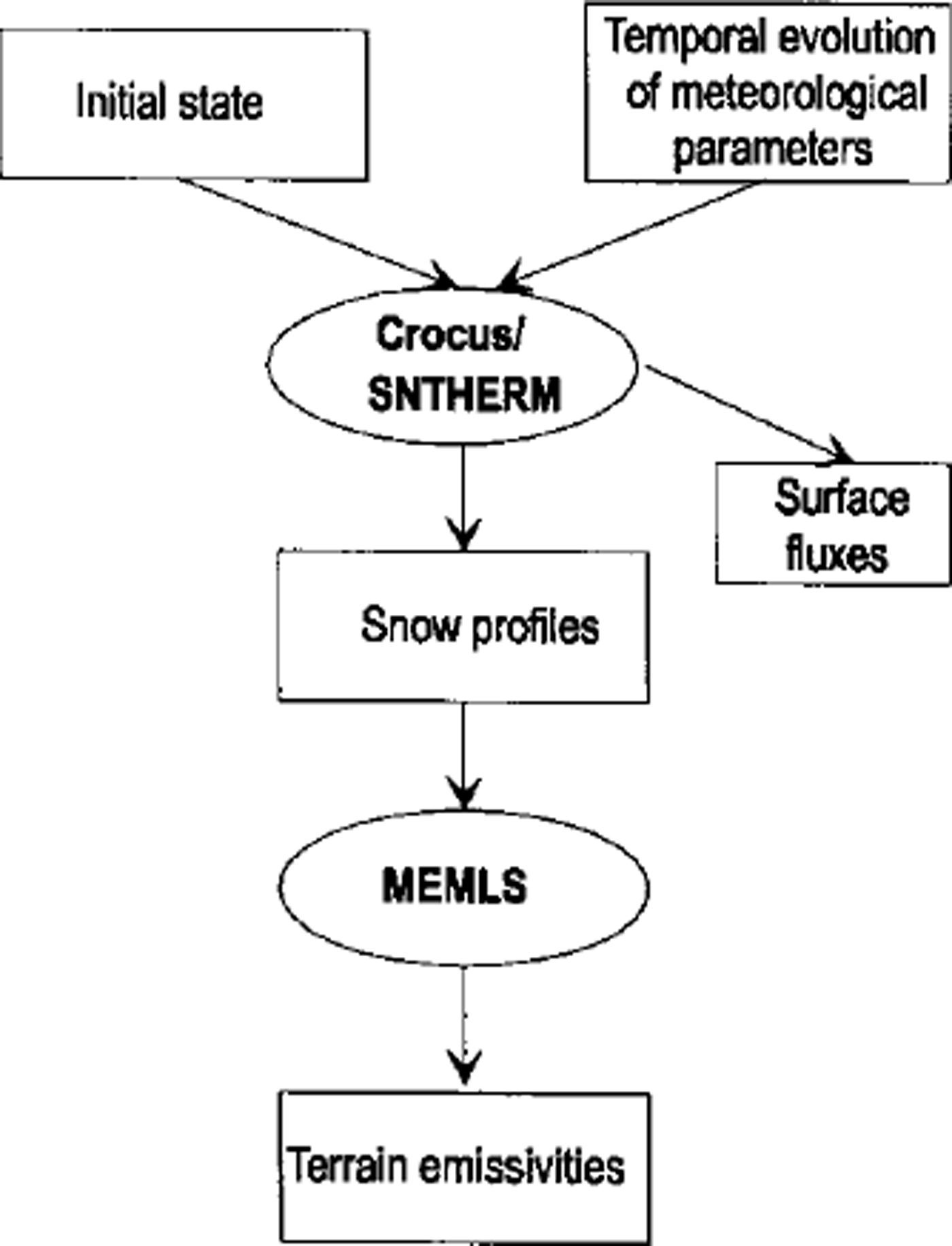
Fig. 1. The snow profiles generated by the snow models Crocus and SNTHERM are used within the microwave model MEMLS to compute the terrain emissvity and brightness temperature at a given frequency, polarization and incidence angle. merical snow-physical model.
Because microwaves are sensitive to snow parameters that are difficult to measure (crusts, texture, liquid-water content, etc.), MEMLS and microwave measurements can help to further develop and validate snowpack models, and therefore contribute to a better understanding of snow physics.
Snowpack Simulation
In Crocus the computed snow profile is characterized by layer number j., layer thickness d, temperature Ts, density A liquid-water content W, two variables for grain description sgran1 and sgran2, date when the layer was created, and the historical grain-description parameter mshist. The grain-description parameters sgranl and sgran2 contain information about the dendricity sphericity and size of the snow grains. For example, it is possible to calculate the optical diameter from these parameters (Reference Brun, David, Sudul and BrunotBrun and others, 1992; Météo France, 1996a). The precipitation date of the layer makes it easy to follow the changes of a selected layer in the snowpack. The mshist parameter indicates if the grains were in contact with liquid water.
In SNTHERM (Reference JordanJordan, 1990) the numerical snow profile is characterized by layer number j., layer thickness d, temperature Ts, density p, liquid-water content W and phase P. The diameter of the hydrometeors ds (provided with the meteorological data) is assumed ds = 0.1mm in accordance with the optical diameter of fresh snow in Crocus. There are two ways of handling the albedo of the snow.
One is to have a constant albedo a (a = 0.78), the other to use a variable approach based on Reference MarksMarks (1988). In this work we used only SNTHERM with constant albedo because the variable-albedo option led to unrealistic behavior.
Memls
The microwave emission model is explained in detail by Reference Wiesmann and MatzlerWiesmann and Matzler (1999). The model covers the frequency range 5–100 GHz, and the snow cover is considered as a stack of n horizontal layers. Each layer is characterized by thickness, correlation length, density, liquid-water content and temperature. Whereas the absorption is computed by a physical model, the scattering coefficient is determined empirically from measured radiometric properties, correlation length and density, based on Reference Wiesmann, Matzler and WeiseWiesmann and others (1998). Similar results are obtained from a physical scattering model (Reference Matzler and WiesmannMatzler and Wiesmann, 1999). The primary output parameter is the upwelling brightness temperature Tb at a given linear polarization, frequency and incidence angle for a given snowpack and ground, and for a given illumination by downwelling sky radiation Tsky. Taking different values of Tsky, the scene emissivity ∊ = (Tb – Tsky)/(Tp – Tsky) can be obtained, as can the effective, physical –scene temperature Tp (see Reference Wiesmann and MatzlerWiesmann and Matzler, 1999, equation (8)).
Connecting the Snow-Physical and Microwave Models
All models describe the snowpack by a stack of homogeneous snow layers, defined by snow-physical parameters Ts, p, W, d and one or two structural parameters. Therefore the output of the snow physical models can almost directly be used as inputs to the microwave model. However, to reduce computation time and limit the number of layers, succeeding layers of similar properties are combined. It is important to note that the description of the snow-grain characteristics differs from model to model. While the microwave model uses a two-point description of the snow texture (by means of a correlation length Pec fitted to an exponential autocorrelation function), the snow models describe the snow by discrete particles. In Reference MatzlerMatzler (1997) it is shown that Pec is not related to the maximum extent, but in all of the cases studied, ρec is close to the minimum characteristic extent of the grains. In the optical range the scattering is also related to this minimum extent. Within the snow-physical models the snow-grain diameters are used to compute the albedo of the snow. Therefore we should be able to make a good guess for ρec from the grain diameter provided by the snow models. Here the correlation length ρec is assumed to be proportional to the grain diameter ds.
Crocus/MEMLS
In Reference Brun, David, Sudul and BrunotBrun and others (1992) a new way of quantifying snow metamorphism was introduced which allowed a description of snow with parameters evolving continuously throughout time. The snow grains are described by sphericity, dendricity and grain-size. In Crocus this information is provided by sgran1 and sgran2 (Météo France, 1996a,Reference Franceb). If we relate the Crocus key snow types, fresh snow (optical grain diameter dcrocus = 0.1mm) and faceted crystals (Crocus = 0.4 mm), with the corresponding correlation lengths of 0.035 and 0.11mm, respectively (Reference WiesmannWiesmann, 1997; Reference Wiesmann, Matzler and WeiseWiesmann and others, 1998), we obtain a relation between Crocus and ρec. Comparing pit profiles of known correlation length and computed Crocus data, we obtain a better assumption by

Sntherm/Memls
In SNTHERM the only texture parameter is the optical grain diameter dSNTHERM. Assuming a linear relation between ρec and dSNTHERM and comparing SNTHERM computed profiles with pit profiles, we obtain best results for:
Model Validation and Data Analysis
In our study we used data of the Swiss Federal Institute of Snow and Avalanche Research (SLF) from the alpine test site, Weissfluhjoch, Davos, Switzerland, at 2540 ma.s.l. The meteorological data were acquired by an automatic station at the test site. Air temperature, relative humidity, wind speed, wind direction, incoming and outgoing short- and longwave radiation, and precipitation are available on a half-hourly basis. The surface-based radiometric measurements (Reference Wiesmann, Strozzi and WeiseWiesmann and others, 1996) were made close to the SLF test site.
Development of the snowpack during the test season
Figure 2b shows the evolution of the observed snowpack at the test site during winter 1995–96 (Reference AmmannAmmann, 1997). The first snow from the beginning of November became slightly wet during the middle of the month, and a hard melt-freeze crust formed at the surface. The larger snowfall of 18–20 November coupled with strong wind from the northwest led to a relatively dense layer of small grains. The snowpack was then subjected to strong temperature-gradient metamorphism until mid-December, resulting in the formation of larger-faceted crystals throughout the snow cover. January was very dry, and a high temperature gradient was observed in the snowpack. From 18 to 23 February, heavy snowfall (46 cm in the test field) with strong wind led to hard layers. In April the snow temperature increased, and in the second half of the month conditions became isothermal. At the end of May the snowpack was still 1 m thick, and 2 weeks later the snow was gone.
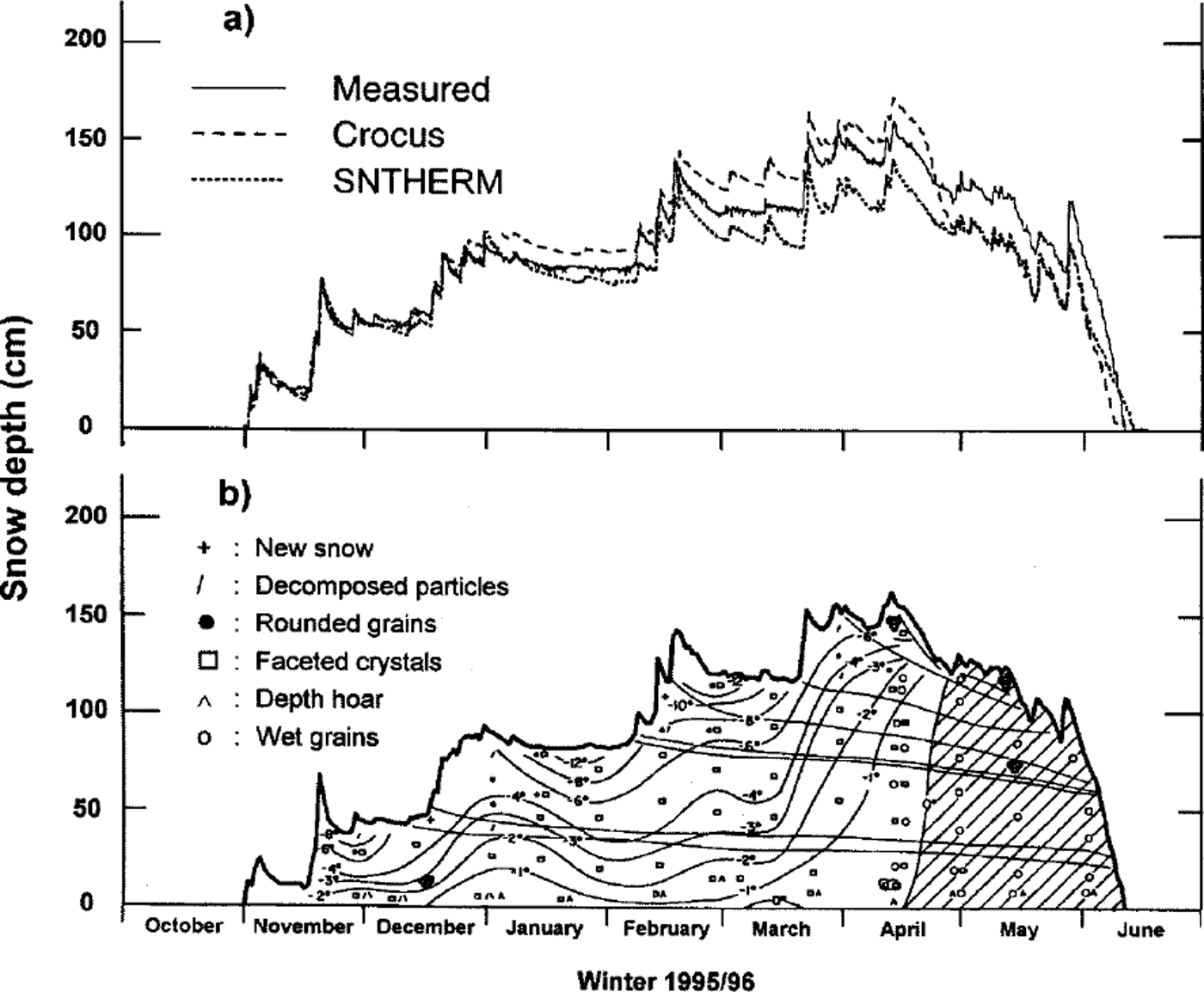
Fig. 2. (a) The development ofthe snow depth as measured by the automatic station (solid line) and computed by Crocus ( dashed line) and SNTHERM (dotted line), ( b) The development of grain shapes, snow depth (cm) and temperature (˚C) of the snowpack at the test site Weissfluhjoch Davos during winter 1995/96 (from Reference AmmannAmmann, 1997).
Evaluation of the temporal behavior of the simulated snowpack
The maximum water equivalent, 462 mm we., measured on 16 April 1996, compares well with the values of 433 and 432 mm simulated by Crocus and SNTHERM, respectively This shows that the models represent the mass balance well even though the difference in snow depth may sometimes be large, as shown in Figure 2a. We should keep in mind that even at a site like Weissfluhjoch, the observed snow depth varies by at least ±10 cm (about ±30 mmwe.) across the study plot. Whereas the differences during the accumulation period are mainly due to the way the models estimate new-snow density, the combination of a decreasing albedo with a strongly increasing shortwave contribution to the energy balance may explain the observed discrepancies during ablation. Comparison of the Crocus albedo with measurements (incoming and outgoing short- and longwave radiation is measured at the test site on a half-hourly basis) shows good agreement: a mean albedo of 0.84 ±0.05 prevails during the accumulation period and decreases steadily to around 0.65 during ablation. Thus, except for the onset of ablation, Crocus simulates the decreasing snow depth quite well during the latter period. Similarly, a constant albedo of 0.78 performs well in SNTHERM, whereas the variable albedo of SNTHERM seems not to represent wet snow conditions very well.
Finally, we would like to address the issue of the energy balance at the surface. As long as no melting occurs, the energy balance is well represented by the snow surface temperature. Fortunately, the latter is accurately measured at Weissfluhjoch (Reference WeilenmannWeilenmann, 1998). Throughout the accumulation period (dry snowpack), both models do equally well, with a tendency to underestimate the surface temperature by a few °C (Reference WiesmannWiesmann, 1998).
For a detailed evaluation of the internal behavior of the snowpack, the reader is referred to the two case studies below, as well as to Reference FierzFierz (1998).
Temporal emissivity behavior βτom Crocus/ MEMLS
Figure 3 shows simulated emissivities at 50° incidence angle for 11, 35 and 94 GHz at both h- and v-polarization vs time based on Crocus profiles. The emissivity is calculated for every simulated snow profile, i.e. at 0500, 0800,1100,1300 and 1500 h UT each day. The soil-snow reflectivity is assumed constant (0.1 at h-pol, 0.05 at v-pol). The soil temperature is assumed equal to the temperature of the lowest layer.
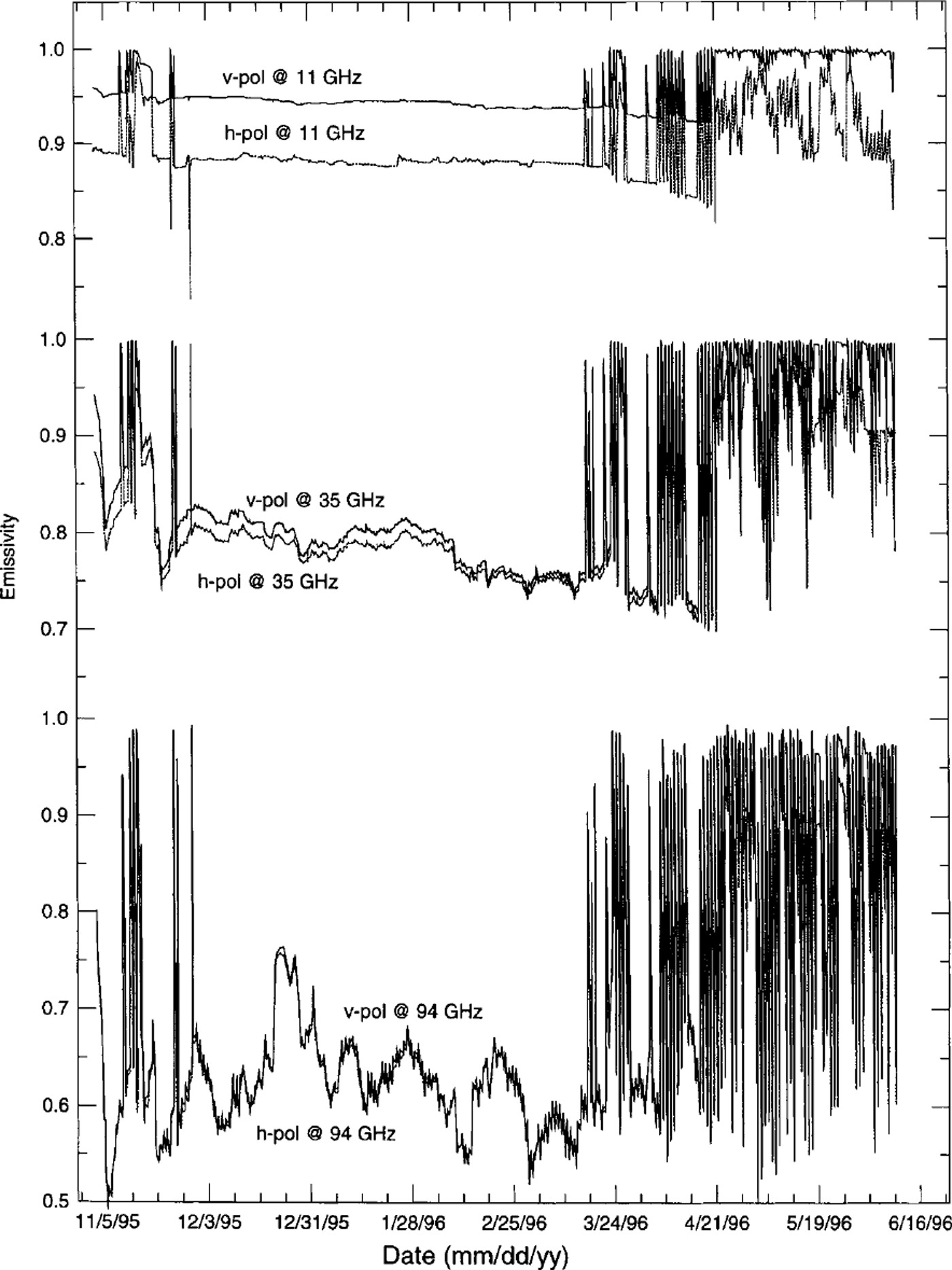
Fig. 3. Snowpack emissivity ev, eh at 50° incidence angle vs time, computed from Crocus profiles. Frequency from top to bottom: 11, 35 and 94 GHz.
At all frequencies four periods can be clearly distinguished. The first period starts on 5 November and lasts until the end of November. In this period the first snowfall events are observed, and during the day the snow is wetted occasionally. During the second period, from the beginning of December until mid-March, the temperature is well below zero, and dry winter snow is observed. In the third period, after mid-March, snow starts to melt during the day and refreezes during the night, leading to dramatic diurnal emissivity changes. Finally, during the fourth period, starting on 19 April, the snow cover contains permanently wet layers and becomes thoroughly wet (Fig. 2b).
The melt events in the first period lead to an increase in absorption in the snowpack and therefore to the characteristic peaks of the emissivity. This effect can be seen during the first period. In addition, some characteristic decreases at 11 GHz h-pol can be observed during wet-snow events. This effect, already seen in the field data of Reference MatzlerMatzler (1987), is due to the enhancement of surface reflection by the wet-snow surface at horizontal polarization. Due to the ongoing metamorphism a decreasing trend in emissivity is observed in the second period. While the emissivity is very stable at 11 GHz, it is variable at 94 GHz. At the higher frequencies, snowfall events and changes in the top layers dominate the signal. During the third period, the emissivity decreases with time due to the strong effect of melt metamorphism on the snow grains. Occasional, and later diurnal, melt events lead again to dramatic emissivity peaks. In the fourth period, the characteristic signature of wet snow is seen as the snowpack becomes isothermal. The sporadic low emissivities are induced by refrozen layers at the top of the snowpack.
In general, the simulation gives a reasonable temporal evolution of the emissivity. However, the polarization difference is underestimated at the higher frequencies.
Temporal emissivity behavior from SNTHERM/ MEMLS
Figure 4 shows simulated emissivities at 50° incidence angle for 11,35 and 94 GHz at both h- and v-polarization based on hourly SNTHERM profiles. The soil-snow reflectivity is assumed constant (0.1 at h-pol, 0.05 at v-pol). The soil temperature is taken from the top soil layer.

Fig. 4. Snowpack emissvity ev, eh at 50° incidence angle, computed from SNTHERM profiles. The frequency from top to bottom: 11, 35 and 94 GHz. separating dendritic and non-dendritic snow:
Again, at all frequencies four periods can be distinguished. They show emissivity similar to that observed in Figure 3, but at slightly different times. More wet-snow events are shown, mainly due to the higher temporal resolution. During the second period, the emissivity behavior at 11 GHz is similar to that in the Crocus/MEMLS simulation. At the higher frequencies the emissivities are of comparable size, but the two major snowfall events (end of 1995 and end of February 1996) dominate the temporal variability much more. In the third period, a characteristic decrease in emissivity of the refrozen snow is expected at all frequencies. A decrease is indeed observed at the beginning of the third period, but after 26 March the emissivity increases to a constant value of 0.77 at 35 and 94 GHz, and to 0.72 at 94 GHz. Due to the diurnal melt-freeze cycles, the emissivity is characteristically high during the day, and decreases again during the night. The fourth period is dominated by the absorption in the completely wet snowpack, leading to high emissivity values.
Case studies with available microwave observations
In this section we focus on two characteristic situations (19 December and 17 January), chosen because of the available microwave measurements and pit profiles (Reference Wiesmann, Strozzi and WeiseWiesmann and others, 1996). The first situation is characterized by several melt-freeze crusts. The microwave measurements are from 19 December; the pit profile is from the day before. The second situation is from a period of low precipitation and low temperatures. Microwave measurements of 17 January are available. The pit profile is from 2 days before. The Crocus and SNTHERM profiles are of the dates and times of the pit profiles. The detailed profiles are shown in Reference WiesmannWiesmann (1998).
19 December 1995
On 18 December the pit profile shows 52 cm of snow, fresh snow on top, underlain by a melt-freeze crust (Knauer layer) at 45 cm, and faceted snow below, in which two additional melt-freeze crusts are embedded at heights of 10 and 33 cm. The densities of the crusts are assumed to be 370 kg m–3 at 10 and 33 cm, and 300 kg m–3 at 45 cm. The Crocus profile shows 64 cm of snow with a mixture of thin, fresh and decomposed snow layers on top, underlain by faceted snow with four layers that underwent melting (indicated by the mshist flag). These layers can be considered as crusts, but compared with the pit profile the densities are much lower.
No grain-type information is offered by SNTHERM. The snow depth of the SNTHERM profile is about 60 cm. The density rises with snow depth from 100 kg m–3 on top to 300 kg m–3 at the bottom of the snowpack. No melt-freeze crusts are indicated.
Both computed profiles show more snow than the snow pits. For the microwave model it is important that the location and properties of density jumps (e.g. crusts), the correlation length and the density profile are in good agreement with the pit profile. The location of the crusts, the type of snow grains and the layer density of the Crocus profile fit the pit profile well, but the density of the crusts is too low. The SNTHERM profile is in good agreement with the pit profile for the grain-size (except for the fresh snow on top, where a comparison is not reasonable). However, the crusts are not observed and the density is too high at the bottom of the pack. Therefore we would expect good agreement of the computed emissivity with the measurement for the simulation with Crocus data. From the SNTHERM data we expect differences due to the high density at the bottom and the lack of crusts.
In Figure 5 the computed emissivity spectra (lines) are compared with the corresponding ground measurements (symbols) at frequencies of 11, 21, 35 and 94 GHz. Figure 5a shows the emissivity computed from the pit profile. The simulation fits the measurements quite well, but the polarization difference at 94 GHz is underestimated. Because of the small penetration depth, at 94 GHz the signal is mainly influenced by the top 10 cm where fresh snow consisting of oblate grains is present. If these grains are not isotropically oriented (e.g. new snow fallen during calm wind conditions (Reference Svendsen, Matzler and GrenfellSvendsen and others, 1987)), we observe different characteristic correlation lengths in the horizontal and vertical directions. This effect is not taken into account in MEMLS. The dashed (v-pol) and dash-dotted (h-pol) lines in Figure 5b show the emissivity computed from the Crocus profile. At v-pol they are in reasonable agreement with the measurement. However, the polarization difference is much smaller for the computed values. If the density of the melt-freeze crust at 45 cm is increased to p = 370 kg m–3 (Knauer layer), the polarization difference increases, and the results (v-pol: solid line; h-pol: dotted line) are in better agreement with the measurements, indicating the importance of accurate modeling of crusts. For the SNTHERM profile (Fig. 5c) a similar effect is noticed. The polarization difference is too small (v-pol.: dashed line; h-pol: dash-dotted line). If a melt-freeze crust is artificially added to the profile at 45 cm, the polarization difference increases to the measured difference. However, the absolute values of the emissivities at 21 and 35 GHz are smaller than observed in situ, while at 94 GHz the model overestimates the emissivity This indicates that the scattering from the top layer is underestimated, whereas the lower layers contribute too much. The reason is a slight error in the modeling of the correlation length or grain-size in some layers.
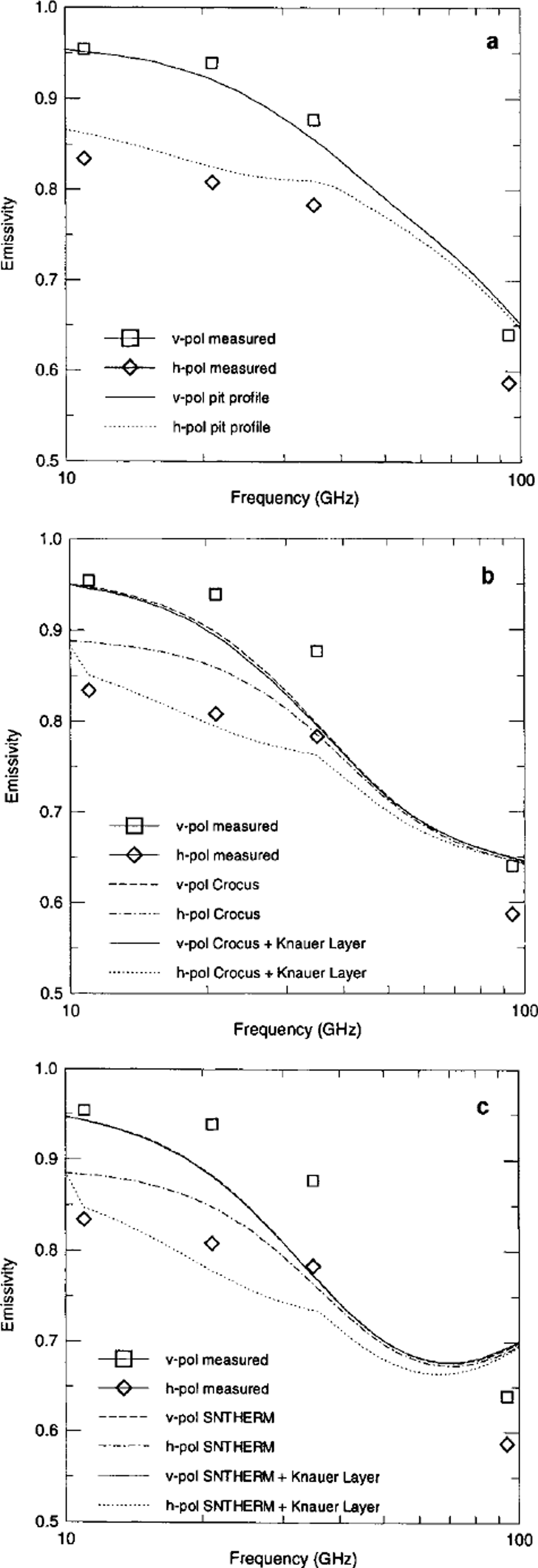
Fig. 5. Computed and measured emissvity spectra, 19 December, for simulations using (a) pit profile, (b) Crocus profile and ( c) SNTHERM profile. Incidence angle 9 = 50°.
17 January 1996
On 15 January a typical winter-snow situation is observed with faceted snow on top, hard densified snow in the middle and coarse-grained snow (depth hoar) at the bottom, and with a strong temperature gradient. The snow depth is 92 cm. Additionally, the pit profile shows a thin surface crust with surface hoar on top. Surface hoar, when subsequently buried by new snow, may form a so-called weak layer within the snowpack. Such layers are a prerequisite for the formation of dangerous snow-slab avalanches. However, neither the surface crust nor the surface hoar is simulated by the snow models. The evolution with time of these snow surface conditions is described by Reference FierzFierz (1998). The temperature gradients of the three models are in good agreement. The Crocus density profile also shows the maximum density in the middle of the snowpack as observed in situ. The snow depth is 94 cm. Although the densities are within a reasonable error range of the pit profile, they are always smaller than the measured densities. The densities of the SNTHERM profile increase with snow depth from 150 to 360 kg m–3. Therefore the characteristic hard, dense area in the middle of the snowpack is not recognized. The snow depth is 80 cm. The grain-sizes from the Crocus profile are rather small compared with the SNTHERM and pit profiles. However, the computed correlation lengths are comparable. Since the density of thick (incoherent) layers has only a minor influence on the microwave signal, we would expect good agreement of the simulated emissivities of both profiles with the in situ measurements.
Indeed, the emissivity spectra of 17 January shown in Figure 6 are in good agreement with the in situ measurements. However, the emissivity at v-polanzation seems to be slightly underestimated. Therefore the polarization difference is smaller than the measured difference. The computed emissivity spectra from Crocus (Fig. 6b) and SNTHERM profiles (Fig. 6c) are in very good agreement with the emissivities computed from the pit profile (Fig. 6a). Again, minor differences are observed at 94 GHz.
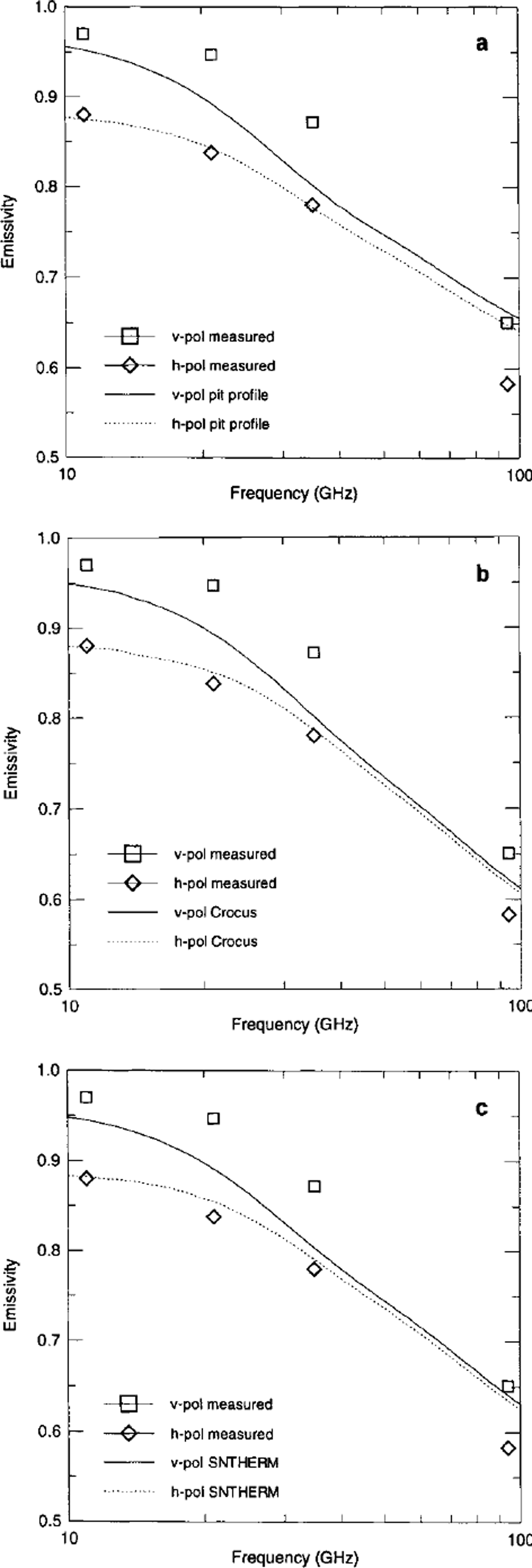
Fig. 6. Computed and measured emissivity spectra, 17 January, for simulations using (a) pit profile, (b) Crocus profile and ( c) SNTHERM profile. Incidence angle 9 = 50°. and snow sections according to Reference Wiesmann, Matzler and WeiseWiesmann and others (1998)) to improve the interface.
Discussion
The snowpack emissivities of both combinations, Crocus/ MEMLS and SNTHERM/MEMLS, are in reasonable agreement with in situ measurements. The results confirm the ability to compute the snowpack emissivity by means of a combined snow-physical and snow-emission model. The computed temporal behavior of the emissivity of winter 1995/96 is reasonable (Figs 3 and 4). Four periods, characterized by the liquid-water content of the snow, are determined, corresponding to fresh snow in autumn, dry winter snow, melted and refrozen snow and isothermal snow. While the first and second periods are dominated by volume scattering due to fresh snow, the other periods are dominated by the strong absorption of wet snow in alternation with strong volume scattering by refrozen surface crusts. The curves of the two combinations behave differently during the second period. While the signal of the SNTHERM/MEMLS model is dominated by the two larger snowfall events (Fig. 4), the signal of the Crocus/MEMLS model shows more variability This effect indicates that the snow models have different ways of computing the grain-size of fresh snow. In the third period, Crocus/MEMLS indicates the characteristic decrease in emissivity due to the refrozen crusts. This effect is less pronounced in SNTHERM/MEMLS. Very good agreement of model computations with ground measurements was obtained for the winter-snow situation of 17 January (Fig. 6). However, two problems arose that need special attention in future:
-
(a) The snow models and the microwave model have different approaches to the characterization of snow texture.
-
(b) The computed polarization difference is often too small.
Problem (a) was discussed earlier in this paper. The assumption that correlation length is linearly related to grain-size gave reasonable results, but it is a purely empirical access and might depend on the situation. There are two ways to improve the interface: (1) adapt the snow-physical model to produce the correlation length, or (2) find an improved conversion algorithm to obtain the correlation length from the available model parameters. The latter, especially the combination with Crocus, looks promising because it provides not only grain-size, but also sphericity, dendncity and mshist. However, more work is needed (analysis of grains according to Reference Brun and PahautBrun and Pahaut (1991),
Considering problem (b), there are two possible reasons for the underestimation of the polarization difference. Firstly, MEMLS treats volume scattering within each layer as a polarization-independent process. This simplification is based on the observations of Reference Wiesmann, Matzler and WeiseWiesmann and others (1998). Nevertheless, volume scattering could be slightly stronger at horizontal polarization, especially if the snow grains show a preference for horizontal alignment, as can occur in fresh snow. Secondly and possibly more importantly, the density profile tends to average the actual vertical density variation, so the interface reflectivities tend to be underestimated. This is especially significant at horizontal polarization if thin crusts or thin weak layers are present. The crusts are not (SNTHERM), or not correctly (Crocus), simulated by the snow models. In Crocus the layers are observed. However, the simulated density of these layers is much lower than we expect from experience. The emissivity computed from both snow profiles underestimates the polarization difference, while the computed emissivity from the pit profile is in agreement with the measurement. If the observed crust at 45 cm is added to the simulated profiles, the polarization difference increases and the simulation is in good (Crocus) and in reasonable (SNTHERM) agreement. In Crocus profiles, crusts of refrozen snow can be located by means of the mshist parameter. This parameter indicates if the grains of a layer have been in contact with liquid water, and if they underwent one or several melt-freeze cycles. Hence, it is possible to identify the crusts in the Crocus profile. In the examples investigated, the density of these layers was similar to that of the neighboring layers, while a realistic density should be distinctly higher. In SNTHERM-simulated profiles there is no possibility of identifying a crust except from its higher density. Nevertheless, the actual sequence of weak and hard layers is very important for the microwave signal and therefore has to be taken into account by the snow model.
In summary, although the snow-physical models are not optimized to be used with the microwave model, promising results are observed. Several improvements of the combined model are indicated:
better physical modeling of densities of crusts and other thin layers
improved interface between the grain descriptions of the physical models and MEMLS
in MEMLS polarization effects should be further studied, especially for isotropic snow.
Conclusions and Outlook
An extended forward model of snowpack emissivity, consisting of the combination of physical snowpack models (SNTHERM and Crocus) with MEMLS, has been implemented and tested against ground-based snowpack and emissivity measurements. We presented comparisons of model snowpacks and observations and detailed analyses of the correspondence between computed and measured emissivity and observed snowpack state. The results show the potential of combined snow-physical and microwave-emission models for understanding snow signatures and developing algorithms for remote sensing of snow. The linear relation between grain-size and correlation length is satisfactory. To obtain better results, however, a better interface must be developed. Microwaves give insight into aspects of the snowpack that the eye cannot see, so the microwave model provides a new dimension in the observation and development of snow physics and snow models. Improvements of these models are needed. To further test and advance emissivity modeling, long-term emissivity measurements should be compared with simulated data.
There are several applications for the combination of snow-physical models with MEMLS:
A promising application is the extension of Crocus by SAFRAN (Système d’Analyse Fournissant des Renseignements Atmosphériques a la Neige; Reference Durand, Brun, Merindol, Guyomarc’h, Lesaffre and MartinDurand and others, 1993). SAFRAN is a sophisticated meteorological model, calculating the input variables for snow-cover simulations in a model topography over large areas (about 1000 km2). A combination of SAFRAN/Crocus with MEMLS offers the possibility of computing the emissivity of larger areas.
The combination with numerical weather forecasts provides the opportunity to simulate emissivity maps. Comparing these maps with real-time emissivity data makes it possible to validate weather forecasts on a large scale. On a local scale it can help to detect objects in, or changes of, the snowpack.
Using historical meteorological information, it is possible to simulate the emissivity of past conditions, providing a tool for re-analyzing historical satellite data.
With accurate knowledge of the surface emissivity it is possible to remotely sense atmospheric parameters from space. To date, however, this technique cannot be used over land, because the emissivity is variable, and thus not well known. MEMLS can contribute to the use of this technique over snow-covered terrain.
MEMLS can help to improve the snow-physical models, especially the quantitative understanding of snow metamorphosis and layer structure.
The presented model combinations can be used to generate fast, simple emission models for microwave remote sensing adapted to specific climate and seasonal conditions.
Acknowledgements
We would like to thank R. Jordan of CRREL for her kind help and patience in answering questions on SNTHERM. The Crocus model was used under licence from Météo France. This work was supported by Snowtools, a European Environment and Climate Project. Financial support was provided by the Swiss Bundesamt für Bildung und Wissenschaft and by the European Commission (contract Nos. BBW 95.0847 and NENV4–CT96–0304).








