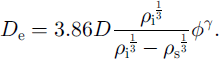Notation

Introduction
Snow can be viewed from two entirely different standpoints: first as a continuum, and second as a particulate medium. The metamorphic processes that profoundly affect mechanical properties are most conveniently examined using the particle approach. In this paper both approaches are used to obtain the diffusion coefficient for snow. The phenomenon of mass transfer in dry snow can play a substantial role in metamorphism because of the high porosity of snow and the possibility of a large temperature gradient. It has also been reported (Reference YosidaYosida and others, 1955) that sublimation is the grain-growth mechanism for dry snow. The mass-transfer rate is proportional to the water-vapor density gradient, which is a function of temperature gradient and mean temperature. The diffusion process in snow is important not only for mass redistribution and grain growth but also for heat transfer when snow is highly porous, accounting for up to 30% of the heat flux calculated using the reasoning of Reference YosidaYosida and others (1955). Reference Albert and McGilvaryAlbert and McGilvary (1992) report that the value actually contributes ω2%, but they assumed vapor to be unsaturated in their modeling of forced air flow.
It is not yet possible to measure the true thermal conductivity of snow because the separate contributions of sensible- and latent-heat transport cannot be isolated. We therefore observe effective rather than absolute values. The effective diffusion coefficient obtained by Reference YosidaYosida and others (1955) is nearly constant for snow densities of 80–510 kg mȡ3. The grain-growth rates obtained by various authors (e.g. Reference Giddings and LaChapelleGiddings and LaChapelle, 1962; Reference De Quervain and KingeryDe Quervain, 1963; Reference AkitayaAkitaya, 1974; Reference MarboutyMarbouty 1980; Reference ColbeckColbeck, 1983; Reference Satyawali and AgrawalSatyawali, 1994) do not support this finding, but these authors assumed a constant value for the diffusion coefficient that controls grain growth. Evidence from the field and laboratory confirms that diffusion mass transfer should decrease with an increase in snow density. Only Reference ColbeckColbeck (1993) and Reference Arons and ColbeckArons and Colbeck (1995) have considered the change in diffusion coefficient with snow density and pore space.
A diffusion coefficient that varies with atmospheric pressure was used in the grain-growth model of Reference Giddings and LaChapelleGiddings and LaChapelle (1962), but it does not show large variation and is independent of snow density. These grain-growth results are consistent with Giddings and LaChapelle’s proposed model because they considered the influence of snow density on grain growth. Their model shows a decrease in grain growth with increase in snow density. Reference De Quervain and KingeryDe Quervain (1963) also used the diffusion coefficient of water vapor into air for his varying-snow-porosity model. The approach taken by these authors varies, and the question of how the diffusion coefficient depends on density remains unresolved (as also suggested by Reference ColbeckColbeck, 1993). For a review of previous theoretical and experimental work done on vapor flow see Reference ColbeckColbeck (1993) and Reference Arons and ColbeckArons and Colbeck (1995). With the aim of determining the diffusion coefficient, we present a simple model and new experimental results on grain-growth rates. Results from several direct measurements of mass transfer (following Reference YosidaYosida and others, 1955) are also presented and discussed.
Theory
Water-vapor diffusion, caused by a temperature gradient, is the dominant mechanism responsible for the process of grain growth. The microscopic temperature gradient between source and sink (Fig. 1) for an infinite number of grains is given by Reference YosidaYosida and others (1955) as

where 2a is the grain length and h ― 2a is the pore length. In Equation (1) it is clear that G0 is always greater than G, but a and h are difficult to measure because grains and pores are not regularly arranged. A hypothetical model for the arrangement of grains and pores within the snow is introduced for better understanding of the water-vapor diffusion process and the actual temperature gradient between snow grains.
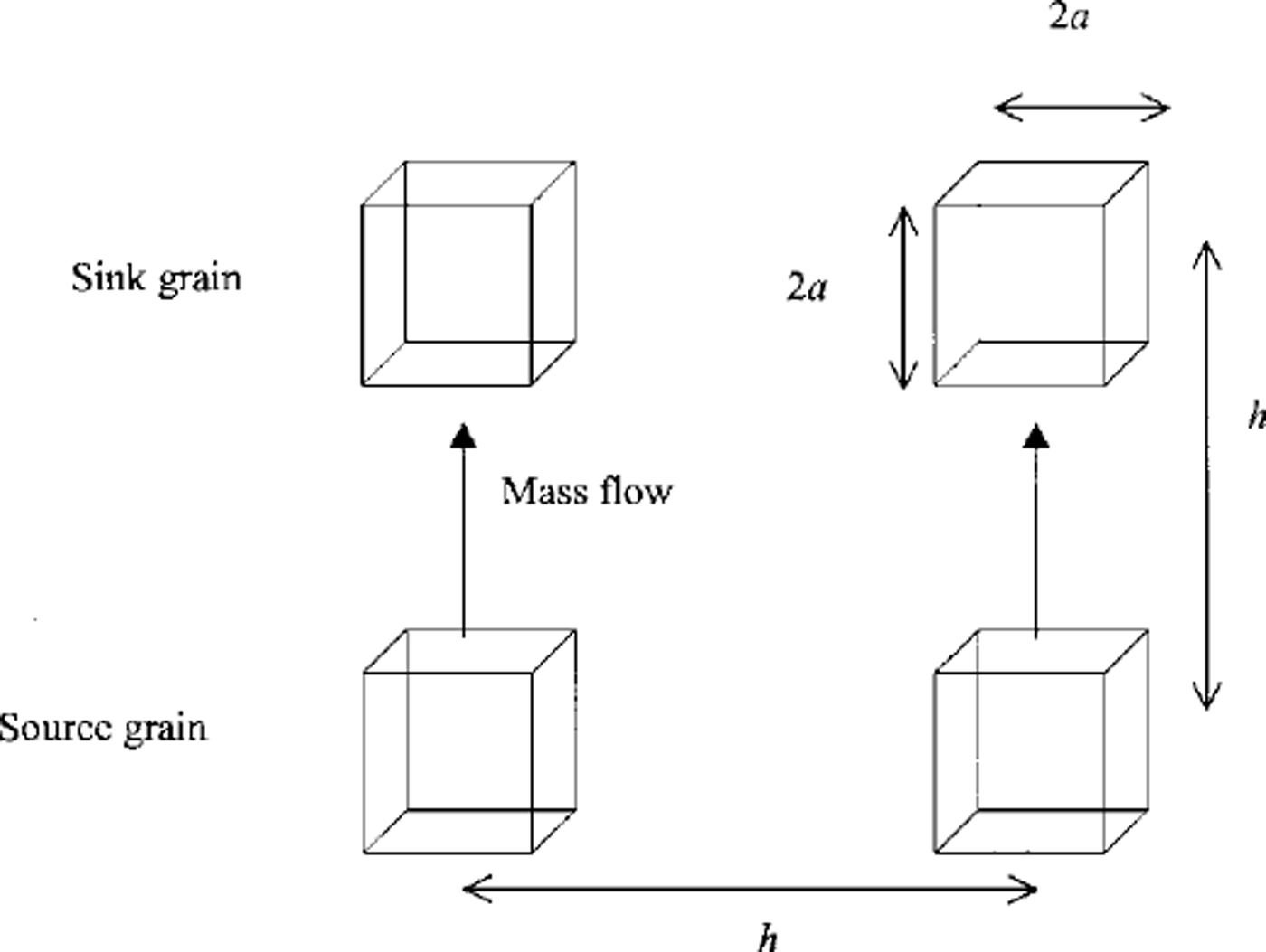
Fig. 1. Packing of snow grains considered for model calculation. Each ice cube represents a grain in this model. Sink and source grains are represented as top and bottom grains.
For cubic packing of snow grains of length 2a and centre-to-centre distance h (Fig. 1), porosity 0 can be obtained as
Porosity can also be expressed in terms of density as 0 = [1 ― (ρs/ρi)}, and therefore Equation (1) can be written as

Using Fick’s law of diffusion, mass flux for snow can be written as
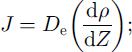
applying the latent-heat equation and ideal gas law, Equation (4) can be written as
We now write an equation for mass transfer between snow grains. As we do not know the value of D∊ for snow, we replace D∊ by D for snow grains, and G by G0. D∊ will be obtained after comparing the measured grain-growth rate with that predicted using the following procedure. The vapor flux between the snow grains (Fig. 1) can be written as
We assume that the mass flux from regions of higher vapor concentration to regions of lower vapor concentration affects the grain growth uniformly, that vapor deposits on the growing-grain surface as a solid ice and that growing grains do not act as a vapor sink. From Equation (5), grain growth can be written as
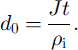
Thus far, we do not know the constant De , and hence Equation (7a) cannot be used to predict grain growth. We therefore replace J by J’ in Equation (7a), and write the grain-growth equation as

Grain-Length Modification Factor
It is known that growth rate is less in high-density than in low-density snow, hence Equation (7b) cannot correctly predict the grain growth. It has been observed that grain length does not vary linearly with porosity, so a non-linear dependency of porosity will be introduced into Equation (7b). The increase in grain length can now be described as dA φr where A and 7 are empirical constants. Equation (7b) can then be written as

The new term φr introduced in Equation (8) will be called the ˚grain-length modification factor". To obtain the value of 7, the following regression analysis has been used.


where n is the number of data points and Sl and s2 are constants.
Grain-Growth Experiments and Model Results
A series of tests on grain growth was performed in the laboratory to evaluate the constants s l and s2
so that 7 could be evaluated. This result can be obtained by comparing Equation (8) with the measured grain length. Grain length was measured according to Reference Satyawali and AgrawalSatyawali (1994), assuming that the equivalent diameter of the long (and the perpendicular
![]() Cl) short axis (c2) is Experimental results gave an approximate value of 4.6 for 7 and 3.86 for A, using Equations (9a) and (9b). The constants were obtained from 47 laboratory experiments conducted on different snow densities. The average temperature, average temperature gradient, initial snow density and initial grain length during these experiments are given in Table 1. SN 1–47 are the results of laboratory experiments, and SN 48–64 are the results of field measurements. In the laboratory, snow samples were subjected to temperature gradients of-21 °C m–1 to –92°C m–1 and temperatures of-2.8° to –18.4°C. These ranges bracket the typical range of field conditions. The laboratory tests were performed mainly on high-density snow.
Cl) short axis (c2) is Experimental results gave an approximate value of 4.6 for 7 and 3.86 for A, using Equations (9a) and (9b). The constants were obtained from 47 laboratory experiments conducted on different snow densities. The average temperature, average temperature gradient, initial snow density and initial grain length during these experiments are given in Table 1. SN 1–47 are the results of laboratory experiments, and SN 48–64 are the results of field measurements. In the laboratory, snow samples were subjected to temperature gradients of-21 °C m–1 to –92°C m–1 and temperatures of-2.8° to –18.4°C. These ranges bracket the typical range of field conditions. The laboratory tests were performed mainly on high-density snow.
Table 1. Results of laboratory experiments (SNI–47) and field measurements (SN48–64) used to determine values of r and A
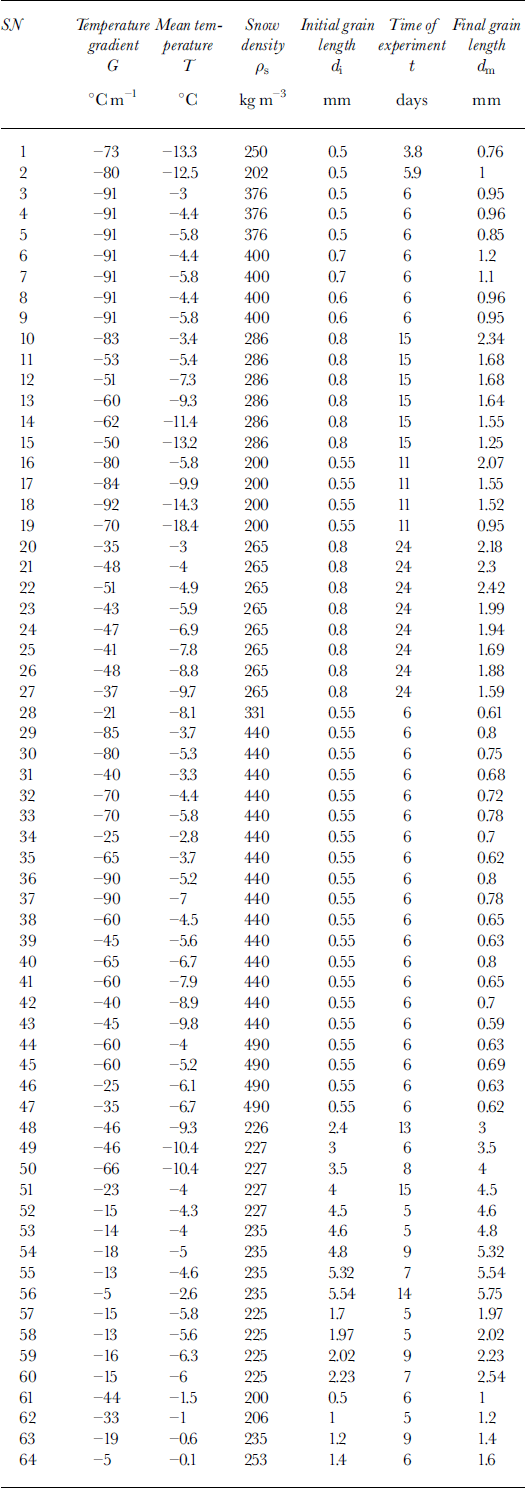
The variation of grain-length modification factor with snow density is shown in Figure 2. Points indicate minimum and maximum error levels associated with the calculation. Reference Lehning, Bartelt, Brown and HestnesLehning and others (1998) incorporated this formulation in the Swiss SNOWPACK model and it gives satisfactory results for the case of an externally applied temperature gradient. The one-dimensional vapor flux can be obtained from Equations (5) and (6), and comparison can then be made between the grain-growth equations (7b) and (8). The resulting expression for the effective diffusion coefficient is

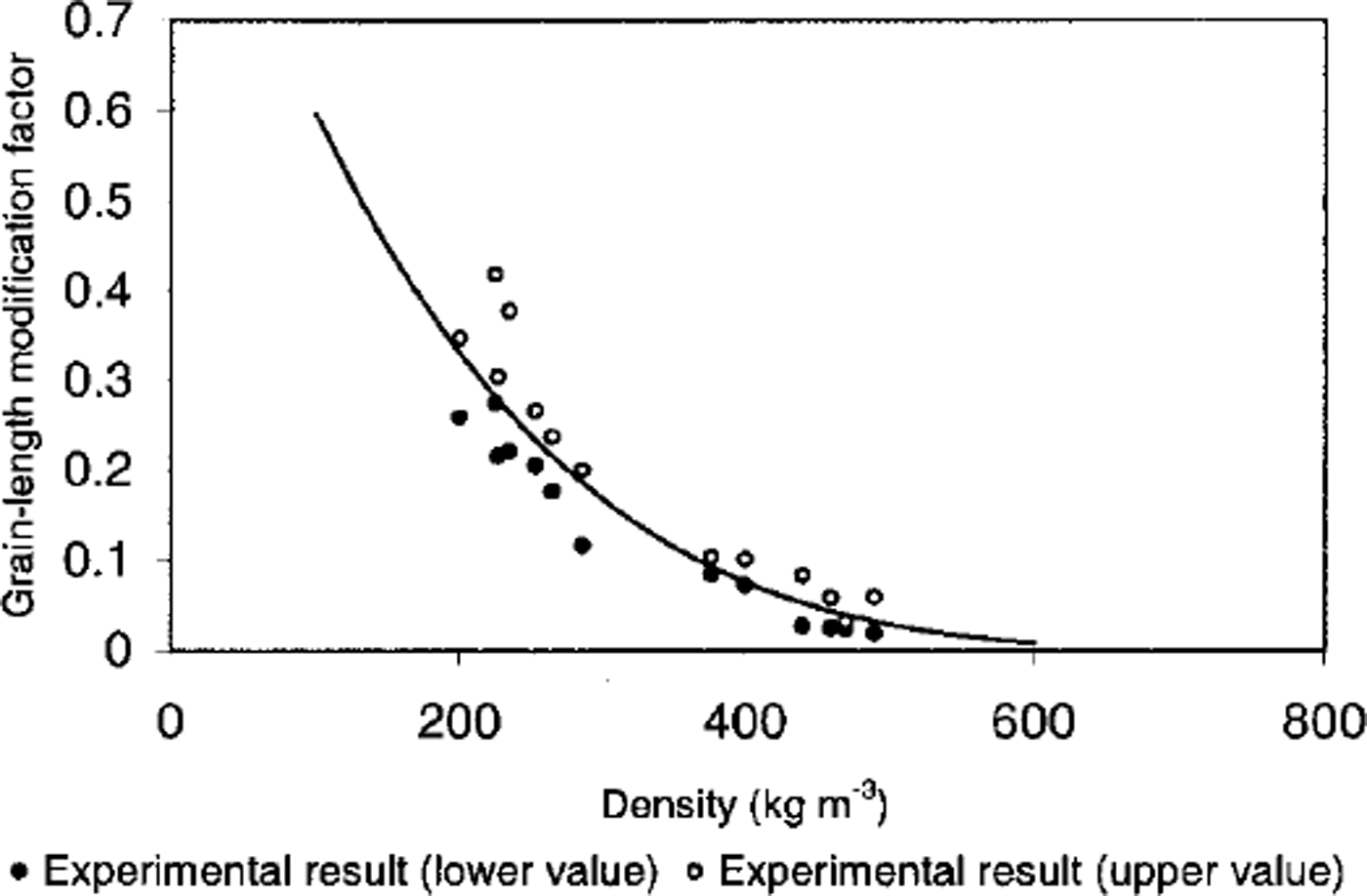
Fig. 2. Plot of grain-length modification factor vs density. Curve shows experimental results obtained in cold laboratory; points represent the maximum error.
Colbeck’s Particle-To-Particle Model
Here the aim is not to discuss the complete theory of Reference ColbeckColbeck (1983, Reference Colbeck1993) but to find a possible solution for the diffusion coefficient based on his three-dimensional model. The grain-growth theory of Reference ColbeckColbeck (1983) computes the temperature difference between source and sink particles, and the resulting mass growth rate is given by
Equation (11) neglects the Kelvin effect, which was shown to be very small (Reference ColbeckColbeck, 1983). Finally, Reference ColbeckColbeck (1983) approximates the change in particle radius for a spherical particle of mean radius a’ as

where dp/dT can be obtained from the Clausius-Clapeyron equation and the ideal gas law (Reference ColbeckColbeck, 1990).
For natural snow, C/a’ and g/a’ are difficult to measure. However, if accurate information about the grain- and pore- length distribution is available, C/a’ and g/a’ can be obtained. Reference ColbeckColbeck (1993) approximated g by h’, the centre-to-centre spacing in a cubic arrangement of particles, and took C/a’ = 1.65(a’/h’)52. Therefore Equation (12) can be expressed as
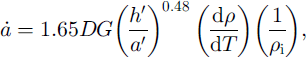
and h’/a’ can be written as [(4π)/3(1–N)] where N = [1 ― (ρs/ρi)} denotes the porosity for a model having spherical grains. The increase in grain length can now be written as
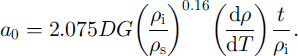
Next we compare the results from the three-dimensional approach of Equation (14) with those from the one-dimensional model of Equation (8). After matching the similar parameters of Equation (14) with those for the one-dimensional model, one obtains

for the effective diffusion coefficient. In arriving at Equation (15) it is important to note that for given values of temperature, temperature gradient and time, the only parameter left after comparing Equation (8) with Equation (14) is snow density, and this contributes differently in the two approaches.
Equation (15) predicts a slight decrease in the effective diffusion coefficient with increasing snow density. The predictions of Equations (10) and (15) are compared in Figure 3. The experimental results clearly show a large variation compared to those based on Equations (10) and (15). However, results from Reference ColbeckColbeck (1993) shown in Figure 4 indicate an increase in diffusion coefficient with increasing snow density, in contrast to the predictions of Equations (10) and (15). The source of the discrepancy is that Reference ColbeckColbeck (1993) approximated vapor flow over an area h2, whereas elsewhere in that contribution he stated that the diffusion coefficient varies with mean pore length. From the present experimental work, the distributions of pore length and grain length are not available to validate Colbeck’s theory; however, experimental results on grain growth give some idea of the influence of snow density on vapor flow.

Fig. 3. Variation of diffusion coefficient of water vapor into snow with change of snow density under temperature gradient.

Fig. 4. Effective diffusion coefficient vs snow density from a particle-to-particleflow model (Reference ColbeckColbeck, 1993).
Diffusion Coefficient by Direct Mass-Loss Experiments
Four direct tests on snow samples were performed in the cold laboratory to obtain the diffusion coefficient. This result can be obtained directly from Equation (4) by measuring the mass loss due to diffusion at a given height of snow sample. The approach is similar to Reference YosidaYosida and others (1955) except that nylon mesh was used in our experiment in place of metallic mesh.
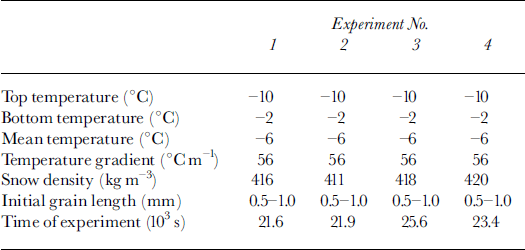
Figure 5 shows a schematic diagram of the experimental set-up. Figure 6 shows the metamorphic apparatus used for the grain-growth and diffusion experiments. For all four experiments the bottom temperature of the apparatus was kept warmer than the top temperature. Vapor pressure was calculated using the latent-heat equation, and mass loss due to diffusion was measured with an electronic weighing machine (AT-201) able to operate at –5°c with a readability of l0–8kg. For all four experiments we have attempted to impose approximately the same values of temperature gradient, mean temperature, snow density and initial grain length. The duration of the experiments was 6–7 hours. Experimental conditions are summarized inTable 2, and the results are presented in Figure 7. Examination of Figure 7 reveals that mass loss at the bottom and top of the sample exceeds that from the sample interior. This discrepancy can be explained as follows: Snow at upper and lower sample boundaries is always in contact with air (low moisture content); because snow is highly saturated, enhanced rates of vapor transfer will occur at the boundaries, yielding increased mass loss from the sample. To avoid this, experiments should be conducted in an isolated system, where total mass can be kept constant. At present we have only these four experimental results for comparison. Finally, I assume that natural convection of air in the snow samples does not occur. However, data presented for SN 1–19 inTable 1 are close to the conditions for natural convection (Reference AkitayaAkitaya, 1974).
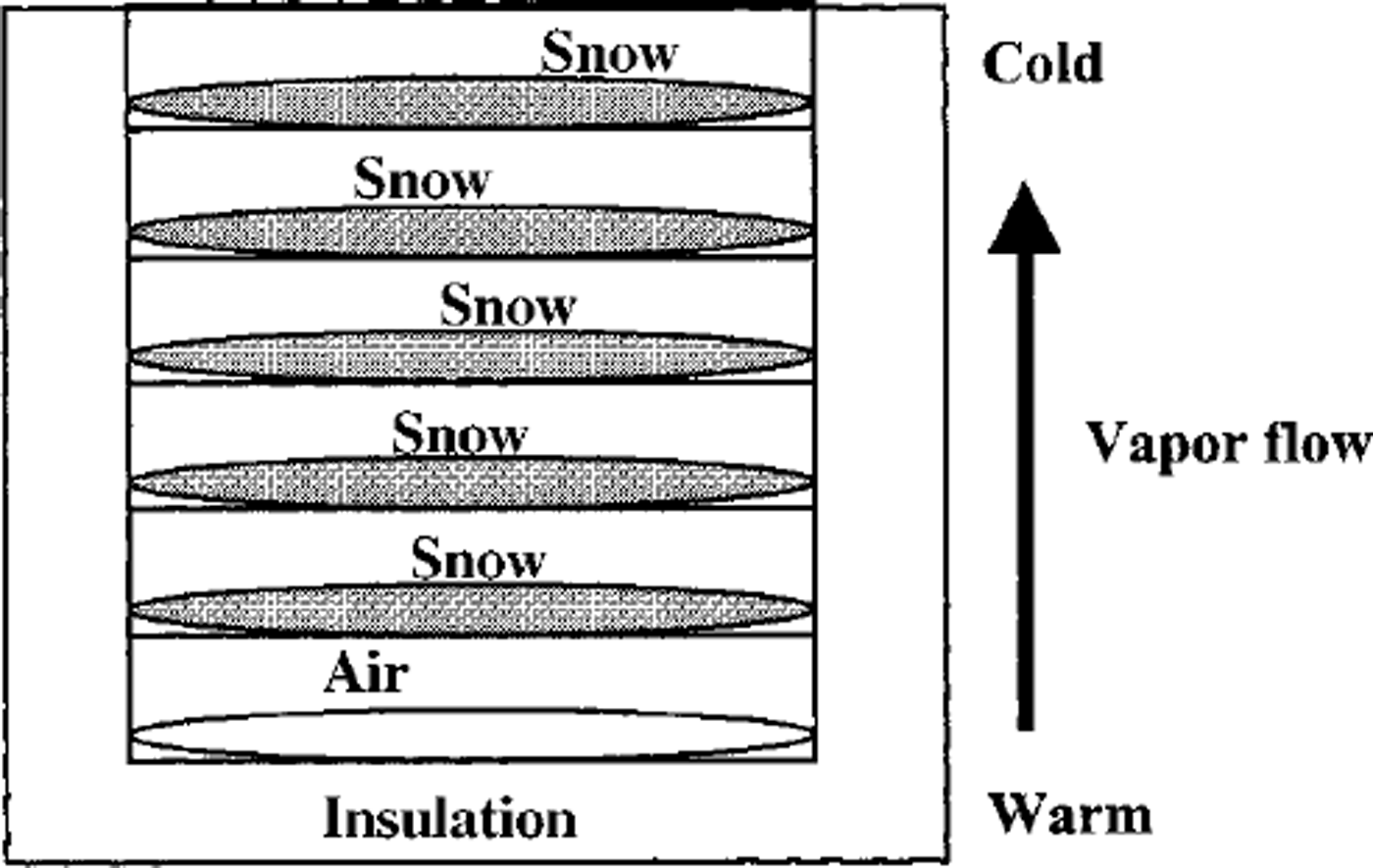
Fig. 5. Schematic diagram of the experimental set-up during direct mmass- loss experiments.

Fig. 6. Metamorphic apparatus used during grain-growth and diffusion experiments.
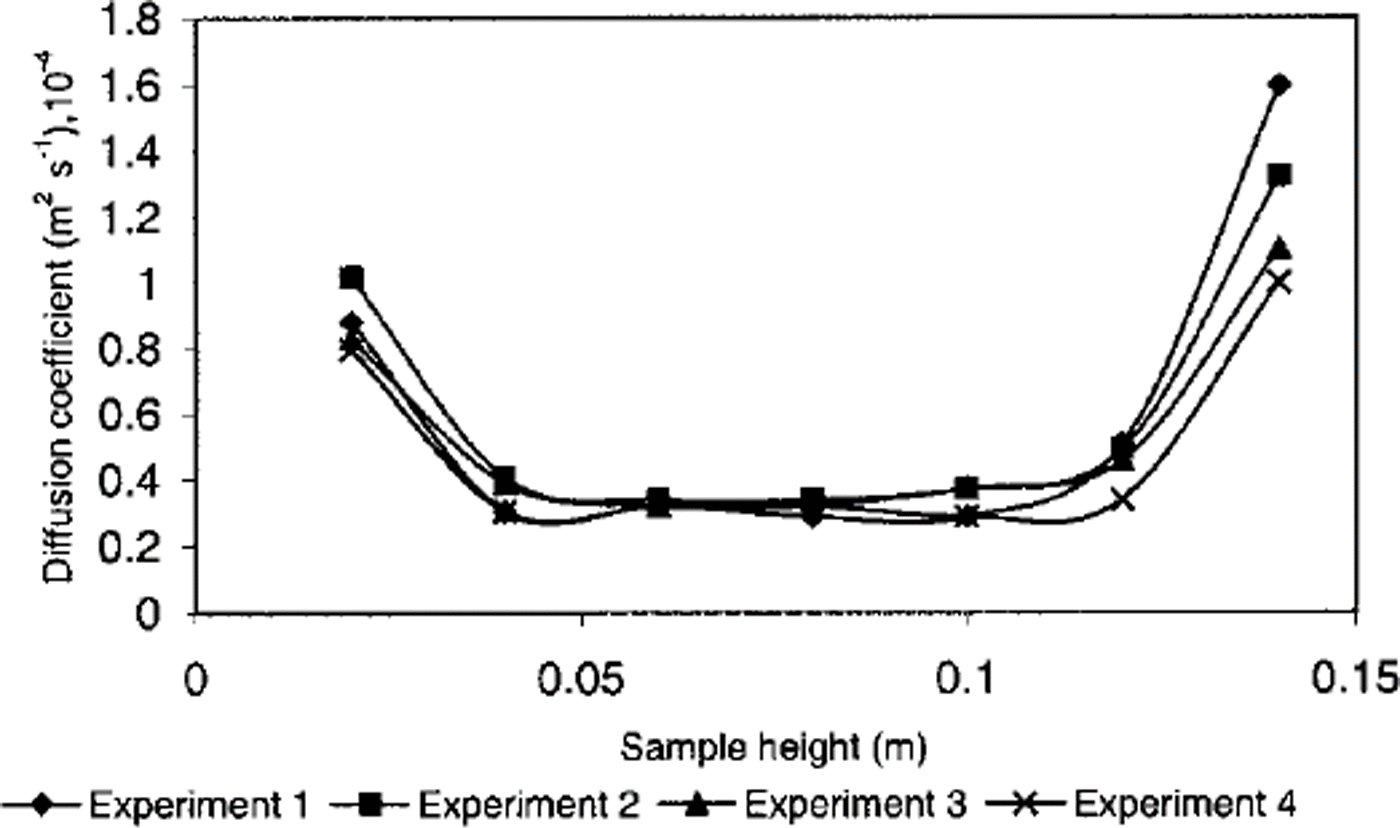
Fig. 7. Variation of diffusion coefficient values from the direct tests, at different heights of the snow sample.
Table 2. Values derived from direct mass-loss experiments
Conclusion
Snow can been treated either as a particulate medium or as a continuum. Under the influence of a temperature gradient the effective vapor-diffusion coefficient for snow is much greater than that for air. The one-dimensional grain-growth model of Reference Satyawali and AgrawalSatyawali (1994) and Equation (10) predict the variation of diffusion coefficient with snow density. Experiments on grain growth have not yet been conducted for snow density in the range 300–400 kg m–3; more experiments will be required to test the model at these values. The theory of Reference ColbeckColbeck (1993) indicates that the diffusion coefficient increases with snow density, but this seems unlikely; in the same paper it is shown that the diffusion coefficient should decrease slowly as pore length increases. Colbeck’s theory explains Reference YosidaYosida and others’ (1955) results on varying snow densities. Similar tests to those of Reference YosidaYosida and others (1955) have been conducted in the present experimental determinations of the diffusion coefficient. Unfortunately, for all four experiments the snow density was essentially the same, and a meaningful comparison cannot be drawn at this stage. In future, the pore- and grain-length distribution should also be monitored for better understanding of vapor flow with time during the grain-growth experiments. For the present, results from the one-dimensional model look satisfactory.
Acknowledgements
I thank Maj. Gen. S. S. Sharma, Director SASE, for permitting me to present this paper at the conference. I would also like to thank G. K. C. Clarke and M. R. Albert for their helpful technical review and useful discussion. I also thank one anonymous reviewer for criticism and comments. This work was supported at SASE, Manali.