Introduction
Snow compaction and changes of physical properties result from irreversible structural changes in the open system. It is unlikely that this process develops at a constant rate throughout the density range, from soft new snow to solid ice. Evolution by stages is more typical of a complex system; its progress is determined by the fact that each successive state is related to the transformation of matrix elements at earlier stages. When compaction has progressed to a certain level, the evolution switches to another mechanism. For snow the critical density values are –140, 330, 550, 710 and 830 kg m–3. The compaction process is divided into a series of stages (Reference MaenoMaeno, 1978; Reference PatersonPatterson, 1994; Reference Frolov, Fedyukin and YamshchikovFrolov and Fedyukin, 1996). Some of them were identified on the basis of changes in the compaction rate observed during constant-stress controlled experiments. Many physical properties of snow, if plotted against snow density, also show noticeable changes near the ˚critical" points. This is true, in particular, of elastic-wave velocity, heat conductivity, electrical resistivity and strength (Reference FrolovFrolov, 1998).
The ice matrix of snow is formed by interconnected ice grains. Any changes in grain number and in connecting elements (bonds) result in changes of snow density and of physical characteristics. It must be taken into account that different arrangements of ice grains (ice-matrix configurations) at the same density can give different physical properties. To obtain reliable data on the physical properties and texture of snow, the representative volume must include ≥ 1000 interconnected grains. Investigations of such large systems, aimed at finding regularities in changes of the snow texture and physical properties during compaction, would necessarily be very complicated. The use of a model which could adequately describe changes in snow physical properties on the basis of possible changes of ice-matrix configuration and of snow-texture parameters could therefore be advantageous.
This paper presents an analytical estimation of certain mechanical properties of dry granular snow and discusses the mechanisms of snow compaction obtained using a theoretical model. The model is based on a spatial regular lattice, formed by points (grains, spherical or polyhedral) connected by rigid bonds. The regular lattice is only an approximation of the actual grain arrangement which is characterized by the probability of local variations in grain dimensions and packing as well as in the thickness and length of intergranular bonds. Nevertheless, the assumption of regular packing allows us to relate the snow compaction and changes in mechanical properties to the changes in textuσl parameters. In particular, it appears possible to relate the critical densities to successive changes in the coordination number (Reference Golubev and FrolovGolubev and Frolov, 1998).
Background
The ice matrix of snow may be represented as a spatial regular lattice, built of spheres with diameter D, placed a distance L apart and interconnected by rigid cylindrical bonds with diameter d. Figure la shows contacting ice grains forming chains in snow texture. Figure 1b-d give examples of spatial regular packing with coordination number (j) equal to 3, 4 and 6, respectively. For these cases the snow density may be described by the following equation (Reference GolubevGolubev, 1982; Reference Golubev and FrolovGolubev and Frolov, 1998):
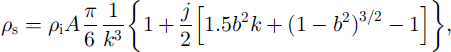
where Pi is the density of solid ice, k = L/D is the index of texture looseness, b = d/D is the index of bond rigidity and A = f(j) is the grain-packing factor, equal to 0.285 at j = 3, to 0.6 at j = 4 and to 1.0 at j = 6.

Fig. 1. Structure of natural, rounded snow (a) and the spatial regular packing with j = 3 (b), j = 4 (c) and j = 6 (d).
Figure 2 shows relative snow density (Ps/Pi) plotted against textural indexes k and b at fixed coordination-number values. The factors that produce the greatest variation in snow density are the coordination number j and the index of texture looseness k. The values of j and k directly influence the number of grains that are principal constituents of the snow texture. Length and, consequently, mass of intergranular bonds also change with changes of k. The dependence of ρs on b results only from changes in the bonds’ mass with changes in their thickness, so this parameter is important for density only in the region of high values of k. Variations of the relative snow density over the possible range of k and of b are as follows: ρs/ρi = 0.07–0.22 at j = 3; ρs/Pi = 0.14–0.47 at j = 4; and ρs/ρi = 0.21–0.72 at j = 6. Average values of ρs/Pi at these coordination numbers are therefore 0.14, 0.30 and 0.50, respectively The latter value coincides precisely with relative density in case of cubical packing j = 6 of spherical grains in contact with each other. At ρs/ρi ≤ 0.14 the coordination number j = 3 (or less). According to Figure 2, for 0.14 ≤ ρs/ρi ≤ 0.22 the coordination-number ice matrix can be 3 (if k ≤ 1.05) or 4 (if k ≤ 1.25). When the relative density is 0.22 ≤ ρs/Pi ≤ 0.47, the coordination number may correspond to 4 (if A: ≤ 1.15) and to 6 (if k ≥ 1.05).

Fig. 2. Relative snow density vs structural parameters.
In Equation (1) the contribution of the bonds to snow density is described by the expression in square brackets multiplied by j / 2 This component may reach 12% of the density at high coordination numbers (j ≥ 6) and high rigidity index (b = 0.5), and with loosely packed grains (k = 1.4), which are unlikely in granular snow. In real snow of medium density b ≤ 0.3 and k ≤ 1.2, where correction for bonds does not exceed 2–5%, a simpler equation may be used to describe the snow density:
It has previously been shown (Reference GolubevGolubev, 1982) that snow mechanical properties, including Young’s modulus E and
Poisson’s ratio v, may be described by structural indexes as follows:
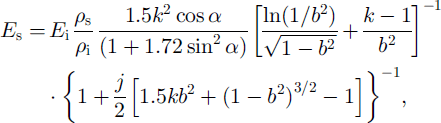
and
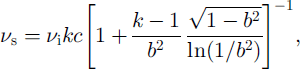
where Ei and vi are Young’s modulus and Poisson’s ratio of solid ice, a is standard deviation of the elements from the symmetry axes in regular packing (a = 30° at j = 3, a = 35° at j = 4 and a = 0° at j ≥ 6) and c is the parameter describing the lateral deformation of the medium as a function of the coordination number j (c = (j ― 2)/4 at j < 6 and c = 1 at j ≥ 6). The expression in square brackets in Equation (3), as in Equation (1), describes the relationship between snow density and bonds’ mass, and in most cases may be omitted as it differs insignificantly from 0 ( ω5%).
It follows from Equations (1–4) and Figure 2 that changes in snow-texture indexes k, b and j must result in essential changes in density and in mechanical properties; the significance of any given parameter may vary with the snow density which also implies changes in the pattern of the relationship between snow density and its properties, and therefore the stadial character of the gravitational compaction process.
Results and Discussion
The snow-compaction mechanism
In granular snow a volume equal to Vs = (πD3/6)(ρf/ρs) corresponds to each grain. The ice grain itself occupies only part of the volume (Vg = πD3/6), while share of pore space is Vp = (πD3/6)[(ρi/ρs)–1]. The ratio between Vp and Vs, and the ratio between pore volume in snow and that of the ice matrix itself, is the coefficient of porosity Kp = Vρ/Vg = [(ρi/ρs) – 1]. According to Equation (2), this coefficient may be described as
Figure 3 demonstrates the relationship between Kp and ρs/ρi and gives the intervals of ρs/ρi for some coordination number j at k = 0.9–1.35. At j = 3 and j = 4, with k = 0.95–1.3, the relative snow density may vary from 0.37 to 0.07, while Kp lies within the range 3 to >10. Therefore, as the volume of pores surrounding each grain is several times greater than the volume of the grain itself, other grains from the overlying layer may easily displace (fall down) into the free space, resulting in rapid snow compaction. At j = 6 and k = 0.95–1.15, the relative density ρs/ρi is 0.6–0.35 and Kp = 0.5–2. The pore volume around grains exceeds the volume of the grain only by a factor of 2 or less. Therefore, other grains from adjacent layers may migrate into pore space only if the packing of grains within a given layer changes its regularity (e.g. in grain aggregates, with k and j having much above average values).
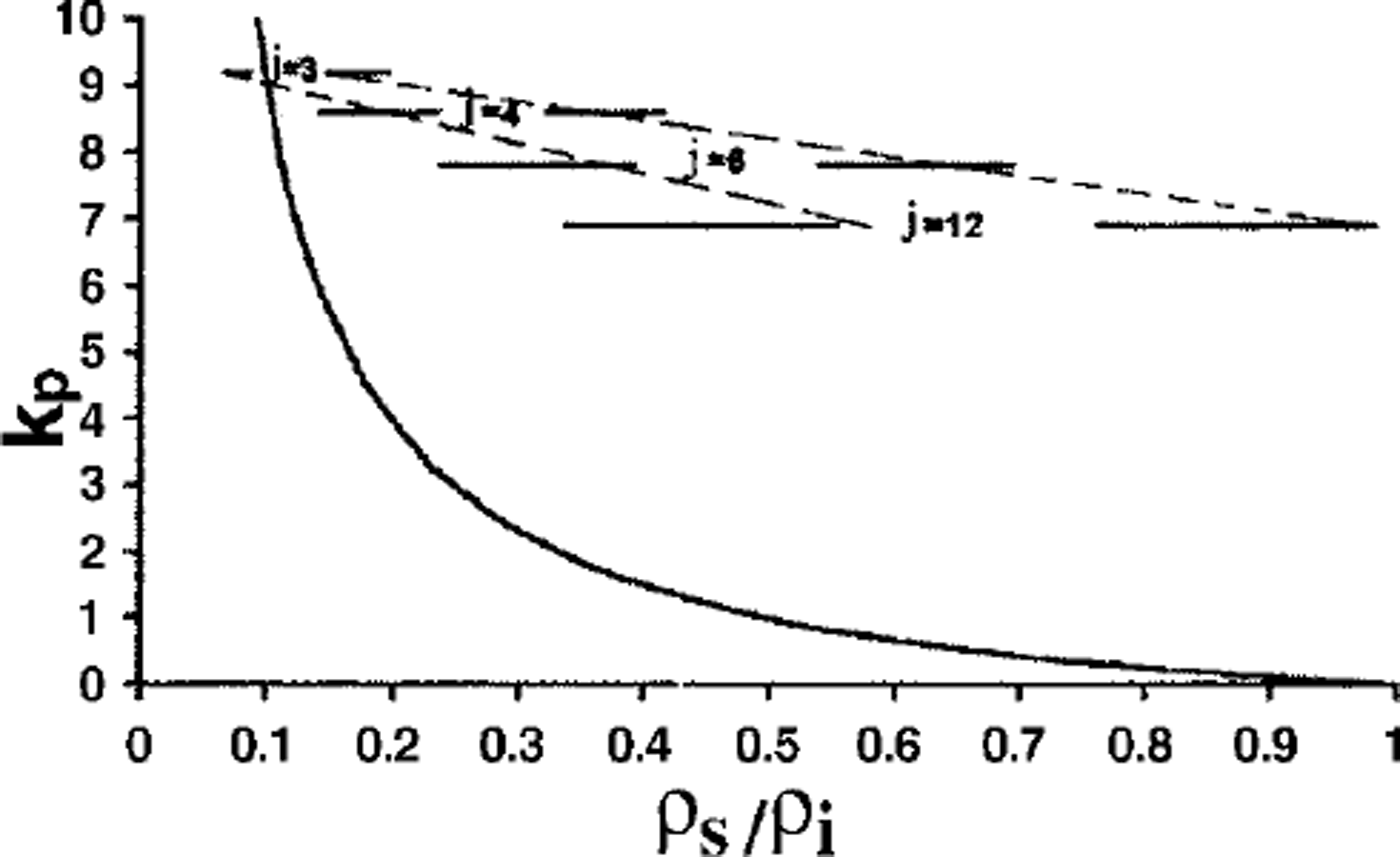
Fig. 3. Porosity factor Kp vs relative snow density. Solid horizontal lines show the ranges ρs/ρi for various coordination numbers. Dashed lines show areas of ρs /ρi at the most probable k values (see text).
Figure 4 shows the number of grains, m, in a layer of thickness L, which must move from their original position in order to accommodate an additional grain. At densities ρs/ρi ≤ 0.25 (which corresponds to Kp ≥ 3) the pore space around each grain within a layer may hold at least one more grain without changes of parent grains’ position in the given layer. Within this area, the snow-compaction mechanism may be considered as a process of accumulation of local disturbances in regular grain arrangement due to movement of grains from adjacent layers. As a result, the index of texture looseness k decreases while coordination number j grows. Finally, there occurs a transition to a higher order of the ice-matrix symmetry.
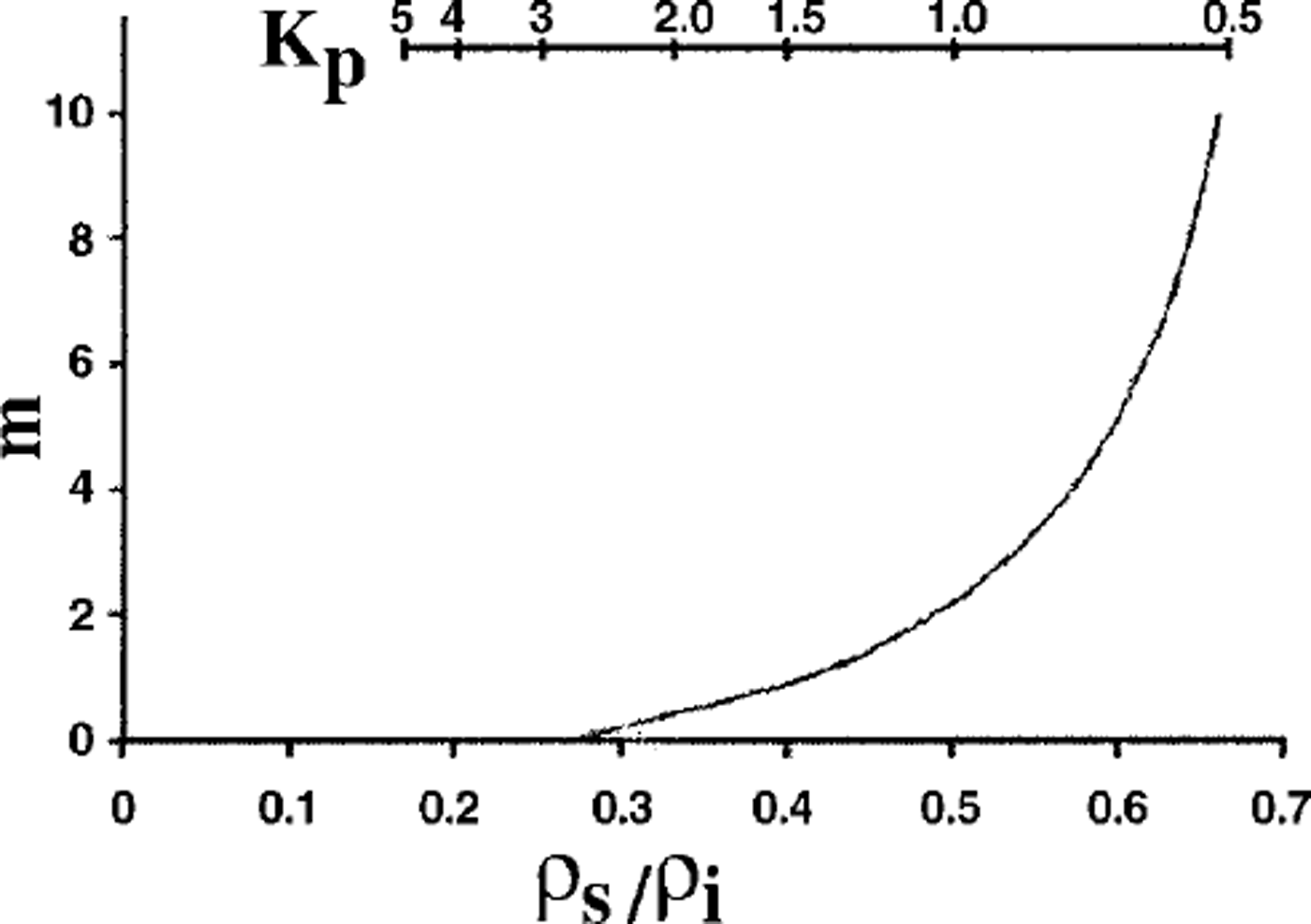
Fig. 4. m(see text) vs ρs/ρi (or Kρ).
At 0.3 ≤ ρs/ρi ≤ 0.5, grains from adjacent layers ˚fall down" only if each one or two grains are displaced from their regular position; this is attributed to the presence of more closely packed aggregates in the layer due to local anomalies of k. Evidently, the rate of compaction will be lower for such a two-stage process.
At ρs/ρi ≥ 0.5 and Kp ≤ 1 grains are practically in contact with each adjacent grain (k ≈ 1.0). The free pore space required for grains to move from one layer to another occurs only in the presence of closely packed aggregates. The grain number in the aggregates must be at least 4 if ρs/ρi = 0.5, and up to 10 if the density increases to ρs/ρi = 0.65. It seems unlikely that individual grains migrate into pore space freed during the formation of such local aggregates. Snow compaction within this density range will be mostly due to grain deformation, which implies a progressive decrease in compaction rate.
It seems that the snow-compaction mechanism changes from the partial breaking of bonds between groups of grains, and migration of those groups into adjacent layers (at j = 3), to individual grain migration within the same layer, resulting in the formation of more closely packed aggregates and subsequent movement of grains from other layers into freed space (at j = 4–6). Finally, at j ≥ 6 the compaction is regulated only by the deformation of grains at their contact. Changes in the mechanism of compaction and of snow-texture transformation are confined to the following densities: ρs/Pi ≤ 0.27 with Kv ≥ 3 and m = 0; ρs/ρi ≈ 0.35 with Kp ≈ 2 and m ≈ 1; and ρs / Pi ≈ 0.5 with Kp ≤ l and m≥3.
Changes in mechanical properties
Reference GolubevGolubev (1982) and Reference Golubev and FrolovGolubev and Frolov (1998) applied the model to calculate Young’s modulus, Poisson’s ratio and the tensile strength of snow. The comparison between the calculated values and the experimental data showed sufficiently good agreement. A primary parameter, however, to be found by experiments is P- and S-wave velocity in a medium. Therefore it seems worthwhile to analyze the model’s potentialities calculating the wave velocities within snow using snow-structure parameters. As a first approximation, we take the familiar equation describing longitudinal wave velocities in a medium:
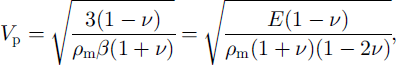
where E is Young’s modulus, Pm is the density, /3 is the volume compressibility coefficient and v is Poisson’s ratio. The relationships between Young’s modulus and Poisson’s ratio as a function of j , k and b (see Equations (3) and (4)) permit transformation of Equation (6) as follows:

where

Results of calculations by this equation for different k, b and j (from loose to compact snow) are shown in Figure 5. The diagrams show the range of velocities Vp for snow with various L and d at fixed density. It is seen that, unlike the density, the elastic-wave velocity depends on both k and b in a similar way. The velocities at the most probable k = 1.2–0.95 and b = 0.15–0.5 (corresponding to natural snow) show good agreement with generalized data of seismic-acoustic studies of snow cover performed in Antarctica, Greenland and the Khibines on the Kola Peninsula, Russia (Reference Frolov and FedyukinFrolov and Fedyukin, 1998). A comparison between velocity diagrams plotted for coordination numbers of grain packing equal to 3, 4 and 6 reveals that they overlap to a certain extent. The reason is that during development of snow-medium texture in which a minor coordination number (e.g. 3 or 4) predominates, the more rigid elements of texture with a greater coordination number (e.g. 4 or 6) are also involved in the medium. This fits well with the concept of snow packing as a large open system and confirms the adequacy of the developed model of grain packing. An inverse problem may also be approached. Using the experimentally measured P- and S-wave velocities and density, it is possible to estimate the snow-texture parameters and snow mechanical properties.

Fig. 5. Velocity of P-waves vs structural parameters.
As in Equation (6), the velocity may be expressed in terms of the medium volume compressibility coefficient /3. As snow is not a continuous medium but a differentially elastic one, it is essential to define its effective volume compressibility taking into account the solid constituents, the pores and the filling substance. Such an approach has been developed by M. Biot, F Gassmann, W. Dobrynin and others (see, e.g., Reference Bourbie, Coussy and ZinsznerBourbie and others, 1986; Reference Dobrymn, Vandelshtein and KozhevinkovDobrynin and others, 1991). In case of snow, which is a gas-saturated porous medium with practically no elastic bonds between solid and gaseous phases, volume compressibility coefficient /3 is
where p is the porosity and βρ, βi and βAk are the coefficients of volume compressibility for pores, ice and skeleton, respectively. Using Equations (3), (4) and (6), we can obtain an equation describing /3sk of snow in terms of its textural parameters:

Results of calculations using Equation (9) are given in Figure 6, which for the first time allows the prediction of changes in the volume compressibility of snow at different coordination numbers and varying k and b values. On the whole, this figure provides a reasonably accurate picture of the variations in snow rigidity. All the specific features mentioned with reference to Vp are typical of fl while calculated values of (3 do not contradict the data obtained for porous ice (-106 MPa–1). From Figure 6 it can be seen that /3 tends to 10˚3 MPa–1 in compact snow and increases to 10˚1 MPa–1 and more in loose granular snow. Figures 2, 5 and 6 show the areas with the most probable magnitudes of physical parameters (ρs/ρi, Vp and /3) based on analysis of j, , b and k values (Reference Golubev and FrolovGolubev and Frolov, 1998). These areas are in good agreement with experimentally measured magnitudes for real snow.

Fig. 6. Bulk compressibility factor vs snow structural parameters.
Conclusion
The presented results of our modelling of dry granular snow texture and physical properties demonstrate the potential of the suggested model. The regular lattice of bounded grains adequately represents the changes in snow physical properties during compaction.
The snow-compaction mechanism includes both deformation of grains (which depends considerably on the bond rigidity b and grain-packing index j) and grain displacement ("falling down" of individual grains and their groups) into free pore spaces in adjacent snow microlayers. During the process, more closely packed aggregates are formed and the texture parameters (first of all, j and k) undergo rapid changes. The prevalence of a certain type of texture transformation is manifested in that the gravitation compaction of snow proceeds in several steps delimited by ˚critical" snow densities.
The suggested analytical relationships between snow density, elastic wave velocity, volume compressibility and snow-texture parameters cover the whole range of possible values. The most probable configuration of the ice matrix in the snow can be deduced both from the snow-texture investigations and from the experimental data on the physical properties, mainly on mechanical parameters.
Acknowledgements
We wish to thank P. B. Grebennikov and D. M. Frolov for important contributions to the preparation of the manuscript. The research was supported in part by the foundation ˚Russian Universities ― Fundamental Research" and the Russian Fund for Basic Research (N98–05–64865).








