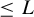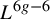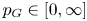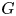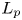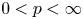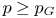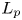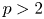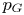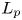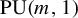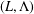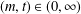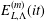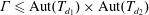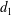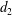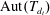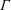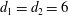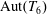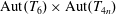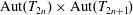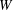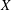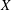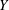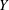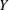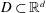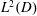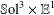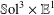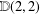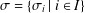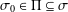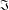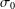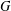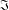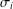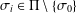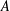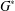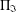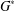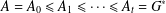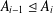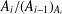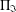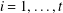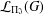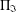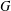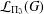43 results
Counting problems from the viewpoint of ergodic theory: from primitive integer points to simple closed curves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTATIONAL FLUID DYNAMICS SIMULATION OF OSCILLATORY FLOW IN PERIODIC MICROPORE STRUCTURES
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 398-400
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
16 - Classics of Elliptic Functions: Selected Properties
- from Part IV - Elliptic Functions: Classics, Geometry, and Dynamics
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 125-172
-
- Chapter
- Export citation
4 - Lattice-Based Integer Factorisation: An Introduction to Coppersmith’s Method
- from Part I - Cryptanalysis
-
- Book:
- Computational Cryptography
- Published online:
- 11 November 2021
- Print publication:
- 02 December 2021, pp 78-105
-
- Chapter
- Export citation
Multiplicative constants and maximal measurable cocycles in bounded cohomology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 3490-3525
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
- Print publication:
- February 2021
-
- Article
- Export citation
ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 118-125
- Print publication:
- August 2020
-
- Article
-
- You have access
- Open access
- Export citation
3 - Coset Progressions and Bohr Sets
-
- Book:
- Introduction to Approximate Groups
- Published online:
- 31 October 2019
- Print publication:
- 14 November 2019, pp 35-53
-
- Chapter
-
- You have access
- Export citation
New Simple Lattices in Products of Trees and their Projections
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 1624-1690
- Print publication:
- December 2020
-
- Article
- Export citation
Relations and trails in lattices of projections in W*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1189-1215
-
- Article
- Export citation
2 - Semihyperbolicity
- from Part One - LECTURES
-
- Book:
- Beyond Hyperbolicity
- Published online:
- 22 June 2019
- Print publication:
- 11 July 2019, pp 25-64
-
- Chapter
- Export citation
On the Weak Order of Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 299-336
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On an Enriques Surface Associated With a Quartic Hessian Surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 213-246
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Three Problems on Exponential Bases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 55-70
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
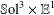 $\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDS
$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 46-56
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
ON THE LATTICE OF
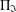 $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-SUBNORMAL SUBGROUPS OF A FINITE GROUP
$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-SUBNORMAL SUBGROUPS OF A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 233-244
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Sonic methods for measuring crystal orientation fabric in ice, and results from the West Antarctic ice sheet (WAIS) Divide
-
- Journal:
- Journal of Glaciology / Volume 63 / Issue 240 / August 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 603-617
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tabling with Sound Answer Subsumption
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 5-6 / September 2016
- Published online by Cambridge University Press:
- 14 October 2016, pp. 933-949
-
- Article
- Export citation