No CrossRef data available.
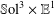 $\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDS
$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-MANIFOLDSPublished online by Cambridge University Press: 04 December 2017
We show that closed 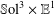 $\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-manifolds are Seifert fibred, with general fibre the torus, and base one of the flat 2-orbifolds
$\mathbb{S}\text{ol}^{3}\times \mathbb{E}^{1}$-manifolds are Seifert fibred, with general fibre the torus, and base one of the flat 2-orbifolds 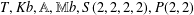 $T,Kb,\mathbb{A},\mathbb{M}b,S(2,2,2,2),P(2,2)$ or
$T,Kb,\mathbb{A},\mathbb{M}b,S(2,2,2,2),P(2,2)$ or 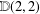 $\mathbb{D}(2,2)$, and outline how such manifolds may be classified.
$\mathbb{D}(2,2)$, and outline how such manifolds may be classified.