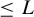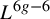1 Introduction
Let us begin our discussion by recalling a classic result in number theory: the prime number theorem. According to this theorem, the number
![]() $\pi (N)$
of positive prime integers p such that
$\pi (N)$
of positive prime integers p such that
![]() $p \leq N$
satisfies the following asymptotic estimate as
$p \leq N$
satisfies the following asymptotic estimate as
![]() $N \to \infty $
,
$N \to \infty $
,
where the symbol
![]() $\sim $
represents the fact that the following identity holds:
$\sim $
represents the fact that the following identity holds:
Analogous results also hold in the setting of hyperbolic surfaces. A closed geodesic on a hyperbolic surface is said to be primitive if it cannot be represented as a concatenation of multiple copies of a shorter closed geodesic. Given a closed, oriented hyperbolic surface X and a parameter
![]() $L> 0$
, denote by
$L> 0$
, denote by
![]() $c(X,L)$
the number of non-oriented, primitive closed geodesics on X of length
$c(X,L)$
the number of non-oriented, primitive closed geodesics on X of length
![]() $\leq L$
. The prime geodesic theorem states that, for any closed, connected, oriented hyperbolic surface X, the following asymptotic estimate holds as
$\leq L$
. The prime geodesic theorem states that, for any closed, connected, oriented hyperbolic surface X, the following asymptotic estimate holds as
![]() $L \to \infty $
,
$L \to \infty $
,
This result shows in particular that the asymptotics of
![]() $c(X,L)$
as
$c(X,L)$
as
![]() $L \to \infty $
do not depend on the geometry of X nor on its topology. The first proof of this theorem was given by Huber and Selberg using analytic methods. See [Reference BuserBus92, Ch. 9] for a detailed discussion of this proof. A dynamical proof of this result for more general negatively curved manifolds was given by Margulis in [Reference MargulisMar70]; this proof relates the exponential growth rate of the counting function of periodic orbits to the topological entropy of the geodesic flow on the manifold.
$L \to \infty $
do not depend on the geometry of X nor on its topology. The first proof of this theorem was given by Huber and Selberg using analytic methods. See [Reference BuserBus92, Ch. 9] for a detailed discussion of this proof. A dynamical proof of this result for more general negatively curved manifolds was given by Margulis in [Reference MargulisMar70]; this proof relates the exponential growth rate of the counting function of periodic orbits to the topological entropy of the geodesic flow on the manifold.
In the setting of hyperbolic surfaces, we can push our curiosity even further. A closed geodesic on a hyperbolic surface is said to be simple if it does not intersect itself. Given a closed, connected, oriented hyperbolic surface X and a parameter
![]() $L>0 $
, denote by
$L>0 $
, denote by
![]() $s(X,L)$
the number of simple closed geodesics on X of length
$s(X,L)$
the number of simple closed geodesics on X of length
![]() $\leq L$
. What are the asymptotics of this quantity as
$\leq L$
. What are the asymptotics of this quantity as
![]() $L \to \infty $
? Do they depend on the geometry of X? Do they depend on the topology of X?
$L \to \infty $
? Do they depend on the geometry of X? Do they depend on the topology of X?
These questions, which a priori seem very similar to those answered by the prime geodesic theorem, remained out of reach for quite a long time. The analytic perspective of Huber and Selberg was not of much use in this setting as it could not distinguish simple closed geodesics among primitive ones. Some progress toward answering these questions was made by Birman and Series [Reference Birman and SeriesBS85], McShane and Rivin [Reference McShane and RivinMR95a, Reference McShane and RivinMR95b], and Rivin [Reference RivinRiv01]. The first major breakthrough would come through the work of Mirkzakhani, who, in her thesis [Reference MirzakhaniMir04], proved the following result.
Theorem 1.1. [Reference MirzakhaniMir08b, Theorem 1.1]
Let X be a closed, connected, oriented hyperbolic surface of genus
![]() $g \geq 2$
. Then, there exists
$g \geq 2$
. Then, there exists
![]() $s(X)> 0$
such that the following asymptotic estimate holds as
$s(X)> 0$
such that the following asymptotic estimate holds as
![]() $L \to \infty $
:
$L \to \infty $
:
Mirzakhani’s proof of Theorem 1.1 uses ergodic theory in a crucial way. Her proof also makes important use of a couple of other breakthroughs in her work: her formulas for the total Weil–Petersson volumes of moduli spaces and her integration formulas over moduli space.
The tools developed by Mirzakhani in her thesis have broad-ranging consequences in many fields of mathematics. Perhaps most well known is her novel proof of Witten’s conjecture on intersection numbers of psi classes on moduli space of Riemann surfaces [Reference WittenWit91]. On a simpler note, let us highlight the following concrete consequence of her work.
Theorem 1.2. [Reference MirzakhaniMir08b, Corollary 1.4]
On any closed, oriented hyperbolic surface of genus
![]() $2$
, it is
$2$
, it is
![]() $48$
times more likely for a random long simple closed geodesic to be non-separating rather than separating.
$48$
times more likely for a random long simple closed geodesic to be non-separating rather than separating.
The main goal of this survey is to give a detailed account of Mirzakhani’s proof of Theorem 1.1 aimed at non-experts. We will draw inspiration from classic primitive lattice point counting results in homogeneous dynamics. Although we will cover the necessary background, the focus will be on understanding how the general principles that drive the proof in the case of lattices also apply in the setting of hyperbolic surfaces. In particular, we will take for granted several fundamental results about Teichmüller spaces and mapping class groups and focus on understanding their applications.
1.1 Organization of this survey
In §2, we study counting problems for primitive lattice points in the Euclidean plane. This discussion will later guide the proof of Theorem 1.1. In §3, we cover the background material on hyperbolic surfaces, Teichmüller spaces, and simple closed curves needed to understand the proof of Theorem 1.1. In §4, we discuss Mirzakhani’s famous formulas for the total Weil–Petersson volumes of moduli spaces and her famous integration formulas over moduli space. In §5, we give a complete proof of Theorem 1.1. In §6, we give a brief overview of several counting results for closed curves on surfaces and other related objects that have been proved since the debut of Mirkzakani’s thesis.
1.2 Other surveys
For a review of similar topics from a more algebro-geometric perspective, see [Reference WolpertWol13]. For a survey covering the full range of Mirzakhani’s outstanding research beyond the few results discussed here, see [Reference WrightWri20]. For discussions of geodesic counting theorems from the point of view geodesic currents, see [Reference Erlandsson and SoutoES22, Reference Erlandsson and UyanikEU20].
2 Counting primitive lattice points in the Euclidean plane
2.1 Outline of this section
In this section, we study counting problems for primitive lattice points in the Euclidean plane. The techniques introduced in this section will serve as a rough guide for the proof of Theorem 1.1 that will be discussed in §5.
2.2 Counting primitive integer points
Consider the integer lattice
![]() $\mathbb {Z}^2 \subseteq \mathbb {R}^2$
. In analogy with the definition of prime numbers, a vector
$\mathbb {Z}^2 \subseteq \mathbb {R}^2$
. In analogy with the definition of prime numbers, a vector
![]() $v \in \mathbb {Z}^2$
is said to be primitive if it cannot be written as a non-negative integer multiple of another vector in
$v \in \mathbb {Z}^2$
is said to be primitive if it cannot be written as a non-negative integer multiple of another vector in
![]() $\mathbb {Z}^2$
. Equivalently, a vector
$\mathbb {Z}^2$
. Equivalently, a vector
![]() $v = (a,b) \in \mathbb {Z}^2$
is said to be primitive if the greatest common divisor of a and b is
$v = (a,b) \in \mathbb {Z}^2$
is said to be primitive if the greatest common divisor of a and b is
![]() $1$
. Denote by
$1$
. Denote by
![]() $\smash {\mathbb {Z}^2_{\mathrm {prim}}} \subseteq \mathbb {Z}^2$
the subset of all primitive vectors of
$\smash {\mathbb {Z}^2_{\mathrm {prim}}} \subseteq \mathbb {Z}^2$
the subset of all primitive vectors of
![]() $\mathbb {Z}^2$
. See Figure 1. Notice
$\mathbb {Z}^2$
. See Figure 1. Notice
![]() $\smash {\mathbb {Z}^2_{\mathrm {prim}}} \subseteq \mathbb {Z}^2$
is not a sublattice, not even a subgroup. Denote by
$\smash {\mathbb {Z}^2_{\mathrm {prim}}} \subseteq \mathbb {Z}^2$
is not a sublattice, not even a subgroup. Denote by
![]() $\|\cdot \|$
the Euclidean norm on
$\|\cdot \|$
the Euclidean norm on
![]() $\mathbb {R}^2$
. For every
$\mathbb {R}^2$
. For every
![]() $L>0$
, consider the counting function
$L>0$
, consider the counting function

Figure 1 Primitive vectors of the integer lattice
![]() $\mathbb {Z}^2$
(colour online).
$\mathbb {Z}^2$
(colour online).
Just as in the case of the counting function
![]() $\pi (N)$
introduced in §1, we are interested in the asymptotics of
$\pi (N)$
introduced in §1, we are interested in the asymptotics of
![]() $p(\smash {\mathbb {Z}^2},L)$
as
$p(\smash {\mathbb {Z}^2},L)$
as
![]() $L \to \infty $
. The main goal of this section is to discuss a rather non-standard proof of the following classic result.
$L \to \infty $
. The main goal of this section is to discuss a rather non-standard proof of the following classic result.
Theorem 2.1. The following asymptotic estimate holds as
![]() $L \to \infty $
:
$L \to \infty $
:
To prove Theorem 2.1, we begin by rewriting the counting function
![]() $p(\mathbb {Z}^2,L)$
in a more convenient way. More concretely, notice that for every
$p(\mathbb {Z}^2,L)$
in a more convenient way. More concretely, notice that for every
![]() $L> 0$
,
$L> 0$
,
 $$ \begin{align*} p(\smash{\mathbb {Z}^2},L) &= \# \{v \in \smash{\mathbb {Z}^2_{\mathrm{prim}}} \colon \| v \| \leq L \} \\ &= \# \bigg\lbrace v \in \smash{\mathbb {Z}^2_{\mathrm{prim}}} \colon \bigg\| \dfrac{1}{L} \cdot v \bigg\| \leq 1 \bigg\rbrace \\ &= \# \bigg\lbrace v \in \dfrac{1}{L} \cdot \smash{\mathbb {Z}^2_{\mathrm{prim}}} \colon \| v \| \leq 1 \bigg\rbrace. \end{align*} $$
$$ \begin{align*} p(\smash{\mathbb {Z}^2},L) &= \# \{v \in \smash{\mathbb {Z}^2_{\mathrm{prim}}} \colon \| v \| \leq L \} \\ &= \# \bigg\lbrace v \in \smash{\mathbb {Z}^2_{\mathrm{prim}}} \colon \bigg\| \dfrac{1}{L} \cdot v \bigg\| \leq 1 \bigg\rbrace \\ &= \# \bigg\lbrace v \in \dfrac{1}{L} \cdot \smash{\mathbb {Z}^2_{\mathrm{prim}}} \colon \| v \| \leq 1 \bigg\rbrace. \end{align*} $$
It is natural then to study the rescaled lattice
![]() $\smash {{1}/{L} \cdot \mathbb {Z}^2_{\mathrm {prim}}} \subseteq \mathbb {R}^2$
as
$\smash {{1}/{L} \cdot \mathbb {Z}^2_{\mathrm {prim}}} \subseteq \mathbb {R}^2$
as
![]() $L \to \infty $
. We do this by means of a measure theoretic approach. For every
$L \to \infty $
. We do this by means of a measure theoretic approach. For every
![]() $L> 0$
, consider the counting measure on
$L> 0$
, consider the counting measure on
![]() $\mathbb {R}^2$
given by
$\mathbb {R}^2$
given by
 $$ \begin{align*} \nu_L^{\mathrm{prim}} := \frac{1}{L^2} \cdot \sum_{v \in \mathbb {Z}_{\mathrm{prim}}^2} \delta_{{1}/{L} \cdot v}. \end{align*} $$
$$ \begin{align*} \nu_L^{\mathrm{prim}} := \frac{1}{L^2} \cdot \sum_{v \in \mathbb {Z}_{\mathrm{prim}}^2} \delta_{{1}/{L} \cdot v}. \end{align*} $$
Notice that if
![]() $B \subseteq \mathbb {R}^2$
denotes the unit ball centered at the origin, then
$B \subseteq \mathbb {R}^2$
denotes the unit ball centered at the origin, then
This setup reduces the original problem of proving an asymptotic estimate for the counting function
![]() $p(\smash {\mathbb {Z}^2},L)$
to the problem of understanding the asymptotic behavior of the measures
$p(\smash {\mathbb {Z}^2},L)$
to the problem of understanding the asymptotic behavior of the measures
![]() $\nu _L^{\mathrm {prim}}$
as
$\nu _L^{\mathrm {prim}}$
as
![]() $L \to \infty $
.
$L \to \infty $
.
2.3 The Lebesgue measure
To develop some intuition, let us first consider a much simpler family of counting measures on
![]() $\mathbb {R}^2$
. For every
$\mathbb {R}^2$
. For every
![]() $L> 0$
, consider the counting measure
$L> 0$
, consider the counting measure
![]() $\nu _L$
on
$\nu _L$
on
![]() $\mathbb {R}^2$
given by
$\mathbb {R}^2$
given by
 $$ \begin{align} \nu_L := \frac{1}{L^2} \cdot \sum_{v \in \mathbb {Z}^2} \delta_{{1}/{L} \cdot v}. \end{align} $$
$$ \begin{align} \nu_L := \frac{1}{L^2} \cdot \sum_{v \in \mathbb {Z}^2} \delta_{{1}/{L} \cdot v}. \end{align} $$
Denote by
![]() $\nu $
the standard Lebesgue measure on
$\nu $
the standard Lebesgue measure on
![]() $\mathbb {R}^2$
. Based solely on geometric intuition, one expects that the following weak-
$\mathbb {R}^2$
. Based solely on geometric intuition, one expects that the following weak-
![]() $\star $
convergence of measures holds:
$\star $
convergence of measures holds:
Indeed, the area of a subset of
![]() $\mathbb {R}^2$
can be computed by counting the number of points of finer and finer lattices that are contained in the set. Recall that the precise definition of weak-
$\mathbb {R}^2$
can be computed by counting the number of points of finer and finer lattices that are contained in the set. Recall that the precise definition of weak-
![]() $\star $
convergence requires that, for every continuous, compactly supported function
$\star $
convergence requires that, for every continuous, compactly supported function
![]() $f \colon \mathbb {R}^2 \to \mathbb {R}$
, the following identity holds:
$f \colon \mathbb {R}^2 \to \mathbb {R}$
, the following identity holds:
The proof of equation (2.3) will be left as an exercise toward the end of this section. See Exercise 2.15. Let us point out for the moment that the main idea behind the proof of equation (2.3) is the fact that every weak-
![]() $\star $
limit point of the sequence of counting measures
$\star $
limit point of the sequence of counting measures
![]() $(\nu _L)_{L> 0}$
is translation invariant.
$(\nu _L)_{L> 0}$
is translation invariant.
2.4 Invariance of counting measures
The discussion above suggests that to prove an analog of equation (2.3) for the counting measures
![]() $(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
, one should try to understand the behavior of the weak-
$(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
, one should try to understand the behavior of the weak-
![]() $\star $
limit points of this sequence. A priori, one has no reason to expect the limit points of this sequence will be translation invariant, as we will conclude a fortiori. Nevertheless, there is still a relevant notion of invariance present in this setting. Indeed, consider the discrete matrix group
$\star $
limit points of this sequence. A priori, one has no reason to expect the limit points of this sequence will be translation invariant, as we will conclude a fortiori. Nevertheless, there is still a relevant notion of invariance present in this setting. Indeed, consider the discrete matrix group
 $$ \begin{align*} \mathrm{SL}(2,\mathbb {Z}) := \left\lbrace \left( \begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right) \in \mathrm{Mat}_{2\times2}(\mathbb {R})\ \bigg\vert \ a,b,c,d \in \mathbb {Z}, ab-cd = 1 \right\rbrace \end{align*} $$
$$ \begin{align*} \mathrm{SL}(2,\mathbb {Z}) := \left\lbrace \left( \begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right) \in \mathrm{Mat}_{2\times2}(\mathbb {R})\ \bigg\vert \ a,b,c,d \in \mathbb {Z}, ab-cd = 1 \right\rbrace \end{align*} $$
acting on
![]() $\mathbb {R}^2$
by linear transformations. The following crucial exercise will provide the notion of invariance we will use to study the counting measures
$\mathbb {R}^2$
by linear transformations. The following crucial exercise will provide the notion of invariance we will use to study the counting measures
![]() $(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
.
$(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
.
Exercise 2.3. Show that the
![]() $\mathrm {SL}(2,\mathbb {Z})$
orbit of the vector
$\mathrm {SL}(2,\mathbb {Z})$
orbit of the vector
![]() $(1,0) \in \mathbb {R}^2$
is precisely
$(1,0) \in \mathbb {R}^2$
is precisely
![]() $\mathbb {Z}^2_{\mathrm {prim}} \subseteq \mathbb {Z}^2$
. Conclude that any weak-
$\mathbb {Z}^2_{\mathrm {prim}} \subseteq \mathbb {Z}^2$
. Conclude that any weak-
![]() $\star $
limit point of the sequence
$\star $
limit point of the sequence
![]() $(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
is
$(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
is
![]() $\mathrm {SL}(2,\mathbb {Z})$
-invariant. Hint: Use Bézout’s identity for greatest common divisors.
$\mathrm {SL}(2,\mathbb {Z})$
-invariant. Hint: Use Bézout’s identity for greatest common divisors.
Exercise 2.3 ensures that any weak-
![]() $\star $
limit point of the sequence
$\star $
limit point of the sequence
![]() $(\nu _L^{\mathrm {prim}})_{L>0}$
is
$(\nu _L^{\mathrm {prim}})_{L>0}$
is
![]() $\mathrm {SL}(2,\mathbb {Z})$
-invariant. Using ergodic theory, we will show this property greatly constrains the possible weak-
$\mathrm {SL}(2,\mathbb {Z})$
-invariant. Using ergodic theory, we will show this property greatly constrains the possible weak-
![]() $\star $
limit points.
$\star $
limit points.
2.5 Ergodic theory
Let
![]() $(X,\mathcal {A})$
be a measurable space and G be a countable group acting on
$(X,\mathcal {A})$
be a measurable space and G be a countable group acting on
![]() $(X,\mathcal {A})$
by measure-preserving transformations. We say a
$(X,\mathcal {A})$
by measure-preserving transformations. We say a
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\mu $
on
$\mu $
on
![]() $(X,\mathcal {A})$
is G-invariant if
$(X,\mathcal {A})$
is G-invariant if
![]() $\mu (g.A) = \mu (A)$
for every measurable subset
$\mu (g.A) = \mu (A)$
for every measurable subset
![]() $A \in \mathcal {A}$
and every
$A \in \mathcal {A}$
and every
![]() $g \in G$
. Furthermore, we say a G-invariant measure
$g \in G$
. Furthermore, we say a G-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $(X,\mathcal {A})$
is G-ergodic if it admits no non-trivial G-invariant subsets, that is, if
$(X,\mathcal {A})$
is G-ergodic if it admits no non-trivial G-invariant subsets, that is, if
![]() $\mu (A) = 0$
or
$\mu (A) = 0$
or
![]() $\mu (X\setminus A) = 0$
for every
$\mu (X\setminus A) = 0$
for every
![]() $A \in \mathcal {A}$
such that
$A \in \mathcal {A}$
such that
![]() $g.A = A$
for every
$g.A = A$
for every
![]() $g \in G$
. Equivalently, a G-invariant measure
$g \in G$
. Equivalently, a G-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $(X,\mathcal {A})$
is ergodic if every G-invariant measurable function is constant almost everywhere with respect to
$(X,\mathcal {A})$
is ergodic if every G-invariant measurable function is constant almost everywhere with respect to
![]() $\mu $
. The following exercise characterizes G-invariant measures on
$\mu $
. The following exercise characterizes G-invariant measures on
![]() $(X,\mathcal {A})$
that are absolutely continuous with respect to a G-ergodic measure.
$(X,\mathcal {A})$
that are absolutely continuous with respect to a G-ergodic measure.
Exercise 2.4. Let
![]() $(X,\mathcal {A})$
be a measurable space and G be a countable group acting on
$(X,\mathcal {A})$
be a measurable space and G be a countable group acting on
![]() $(X,\mathcal {A})$
by measure-preserving transformations. Suppose that
$(X,\mathcal {A})$
by measure-preserving transformations. Suppose that
![]() $\nu $
is a G-ergodic measure on
$\nu $
is a G-ergodic measure on
![]() $(X,\mathcal {A})$
and that
$(X,\mathcal {A})$
and that
![]() $\mu $
is a G-invariant measure on
$\mu $
is a G-invariant measure on
![]() $(X,\mathcal {A})$
that is absolutely continuous with respect to
$(X,\mathcal {A})$
that is absolutely continuous with respect to
![]() $\mu $
. Show that
$\mu $
. Show that
![]() $\mu $
is a non-negative constant multiple of
$\mu $
is a non-negative constant multiple of
![]() $\nu $
. Hint: Show that the Radon–Nikodym derivative of
$\nu $
. Hint: Show that the Radon–Nikodym derivative of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\nu $
is G-invariant and use the G-ergodicity of
$\nu $
is G-invariant and use the G-ergodicity of
![]() $\nu $
to show this derivative is constant.
$\nu $
to show this derivative is constant.
In the setting of counting problems for primitive lattice points, the following ergodicity result will be relevant for us. Although we will not prove it in this survey, let us at least mention that this result can be proved using the ergodicity of the horocycle flow on the unit tangent of the modular curve
![]() $T^1\mathcal {M}_1 := \mathrm {SL}(2,\mathbb {Z}) \backslash \mathrm {SL}(2,\mathbb {R})$
; for a proof of this fact, we refer the reader to [Reference Bekka and MayerBM00].
$T^1\mathcal {M}_1 := \mathrm {SL}(2,\mathbb {Z}) \backslash \mathrm {SL}(2,\mathbb {R})$
; for a proof of this fact, we refer the reader to [Reference Bekka and MayerBM00].
Theorem 2.5. The Lebesgue measure
![]() $\nu $
on
$\nu $
on
![]() $\mathbb {R}^2$
is ergodic with respect to the linear action of
$\mathbb {R}^2$
is ergodic with respect to the linear action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
.
$\mathrm {SL}(2,\mathbb {Z})$
.
2.6 Portmanteau’s theorem
We now state a classic theorem of Portmanteau that gives useful alternative characterizations to the definition of weak-
![]() $\star $
convergence in equation (2.4); for a proof of this result, we refer the reader to [Reference BogachevBog18].
$\star $
convergence in equation (2.4); for a proof of this result, we refer the reader to [Reference BogachevBog18].
Theorem 2.6. Let X be a metric space and
![]() $(\mu _L)_{L>0}$
be a sequence of locally finite Borel measures on X converging in the weak-
$(\mu _L)_{L>0}$
be a sequence of locally finite Borel measures on X converging in the weak-
![]() $\star $
topology to a Borel measure
$\star $
topology to a Borel measure
![]() $\mu $
on X. Then, for every open subset
$\mu $
on X. Then, for every open subset
![]() $U \subseteq X$
,
$U \subseteq X$
,
Additionally, for every compact subset
![]() $K \subseteq X$
such that
$K \subseteq X$
such that
![]() $\mu (\partial K) = 0$
,
$\mu (\partial K) = 0$
,
2.7 Limit points of counting measures
Using Exercises 2.3 and 2.4, and Theorems 2.5 and 2.6, one can greatly restrict the possible weak-
![]() $\star $
limit points of the sequence of counting measures
$\star $
limit points of the sequence of counting measures
![]() $(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
.
$(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
.
Proposition 2.8. Every weak-
![]() $\star $
limit point
$\star $
limit point
![]() $\nu ^{\mathrm {prim}}$
of the sequence of counting measures
$\nu ^{\mathrm {prim}}$
of the sequence of counting measures
![]() $(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
is of the form
$(\smash {\nu _L^{\mathrm {prim}}})_{L>0}$
is of the form
![]() $\nu ^{\mathrm {prim}} = c \cdot \nu $
for some constant
$\nu ^{\mathrm {prim}} = c \cdot \nu $
for some constant
![]() $c\geq 0$
.
$c\geq 0$
.
Proof. Let
![]() $\smash {\nu ^{\mathrm {prim}}}$
be a weak-
$\smash {\nu ^{\mathrm {prim}}}$
be a weak-
![]() $\star $
limit point of the sequence
$\star $
limit point of the sequence
![]() $\smash {(\nu _L^{\mathrm {prim}})_{L>0}}$
. Exercise 2.3 guarantees that
$\smash {(\nu _L^{\mathrm {prim}})_{L>0}}$
. Exercise 2.3 guarantees that
![]() $\smash {\nu ^{\mathrm {prim}}}$
is
$\smash {\nu ^{\mathrm {prim}}}$
is
![]() $\mathrm {SL}(2,\mathbb {Z})$
-invariant. Theorem 2.5 ensures that the Lebesgue measure
$\mathrm {SL}(2,\mathbb {Z})$
-invariant. Theorem 2.5 ensures that the Lebesgue measure
![]() $\nu $
on
$\nu $
on
![]() $\mathbb {R}^2$
is ergodic with respect to the linear action of
$\mathbb {R}^2$
is ergodic with respect to the linear action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
. Thus, by Exercise 2.4, to prove
$\mathrm {SL}(2,\mathbb {Z})$
. Thus, by Exercise 2.4, to prove
![]() $\smash {\nu ^{\mathrm {prim}}} = c \cdot \nu $
for some constant
$\smash {\nu ^{\mathrm {prim}}} = c \cdot \nu $
for some constant
![]() $c \geq 0$
, it is enough to check that
$c \geq 0$
, it is enough to check that
![]() $\smash {\nu ^{\mathrm {prim}}}$
is absolutely continuous with respect to
$\smash {\nu ^{\mathrm {prim}}}$
is absolutely continuous with respect to
![]() $\nu $
.
$\nu $
.
To prove this, let us consider an arbitrary Borel measurable subset
![]() $A \subseteq \mathbb {R}^2$
such that
$A \subseteq \mathbb {R}^2$
such that
![]() $\nu (A) = 0$
. Our goal is to show that
$\nu (A) = 0$
. Our goal is to show that
![]() $\nu ^{\mathrm {prim}}(A) = 0$
. Let
$\nu ^{\mathrm {prim}}(A) = 0$
. Let
![]() $\delta> 0$
be arbitrary. The outer regularity of the Lebesgue measure
$\delta> 0$
be arbitrary. The outer regularity of the Lebesgue measure
![]() $\nu $
guarantees that one can find a countable collection of open squares
$\nu $
guarantees that one can find a countable collection of open squares
![]() $\{B_i\}_{i\in \mathbb{N}}$
such that
$\{B_i\}_{i\in \mathbb{N}}$
such that
To bound
![]() $\nu ^{\mathrm {prim}}(A)$
, let us first give a rough bound of the measure
$\nu ^{\mathrm {prim}}(A)$
, let us first give a rough bound of the measure
![]() $\nu ^{\mathrm {prim}}(B)$
of an arbitrary open square
$\nu ^{\mathrm {prim}}(B)$
of an arbitrary open square
![]() $B \subseteq \mathbb {R}^2$
. Denote by
$B \subseteq \mathbb {R}^2$
. Denote by
![]() $\epsilon> 0$
the side length of B. Notice that, for every
$\epsilon> 0$
the side length of B. Notice that, for every
![]() $L> 0$
,
$L> 0$
,
The set
![]() $L \cdot B \subseteq \mathbb {R}^2$
is an open square of side length
$L \cdot B \subseteq \mathbb {R}^2$
is an open square of side length
![]() $L \cdot \epsilon $
. Suppose
$L \cdot \epsilon $
. Suppose
![]() $L> 0$
is large enough so that this side length satisfies
$L> 0$
is large enough so that this side length satisfies
![]() $L \cdot \epsilon \geq 1$
. Consider the set
$L \cdot \epsilon \geq 1$
. Consider the set
![]() $S \subseteq \mathbb {R}^2$
obtained by taking the union of disjoint open squares of side length
$S \subseteq \mathbb {R}^2$
obtained by taking the union of disjoint open squares of side length
![]() $1/2$
centered at every point
$1/2$
centered at every point
![]() $v \in \mathbb {Z}^2 \cap (L \cdot B)$
. This set is contained in an open square
$v \in \mathbb {Z}^2 \cap (L \cdot B)$
. This set is contained in an open square
![]() $B' \subseteq \mathbb {R}^2$
of side length
$B' \subseteq \mathbb {R}^2$
of side length
![]() $L \cdot \epsilon + 1$
. It follows that
$L \cdot \epsilon + 1$
. It follows that
Putting together equations (2.7) and (2.8), we deduce
We now bound
![]() $\nu ^{\mathrm {prim}}(A)$
. Using the cover in equation (2.6) and the subadditivity of
$\nu ^{\mathrm {prim}}(A)$
. Using the cover in equation (2.6) and the subadditivity of
![]() $\nu ^{\mathrm {prim}}$
, we deduce
$\nu ^{\mathrm {prim}}$
, we deduce
Theorem 2.6 ensures that, for every
![]() $i \in \mathbb{N}$
,
$i \in \mathbb{N}$
,
The identity in equation (2.9) guarantees that, for every
![]() $i \in \mathbb{N}$
,
$i \in \mathbb{N}$
,
Putting together equations (2.10), (2.11), and (2.12), and using the inequality in equation (2.6), we deduce
As
![]() $\delta> 0$
is arbitrary, we conclude
$\delta> 0$
is arbitrary, we conclude
![]() $\nu ^{\mathrm {prim}}(A) = 0$
, thus finishing the proof.
$\nu ^{\mathrm {prim}}(A) = 0$
, thus finishing the proof.
2.8 The space of unimodular lattices
All that remains is to show that the constant
![]() $c \geq 0$
in the conclusion of Proposition 2.8 is positive, independent of the limit point
$c \geq 0$
in the conclusion of Proposition 2.8 is positive, independent of the limit point
![]() $\nu ^{\mathrm {prim}}$
, and actually equal to
$\nu ^{\mathrm {prim}}$
, and actually equal to
![]() $6/\pi ^2$
. We do this by considering an averaging argument over the space of unimodular lattices of
$6/\pi ^2$
. We do this by considering an averaging argument over the space of unimodular lattices of
![]() $\mathbb {R}^2$
up to rotation.
$\mathbb {R}^2$
up to rotation.
By definition, a lattice
![]() $\Lambda \subseteq \mathbb {R}^2$
is the
$\Lambda \subseteq \mathbb {R}^2$
is the
![]() $\mathbb {Z}$
-span of an
$\mathbb {Z}$
-span of an
![]() $\mathbb {R}$
-basis of
$\mathbb {R}$
-basis of
![]() $\mathbb {R}^2$
. A marking of a lattice
$\mathbb {R}^2$
. A marking of a lattice
![]() $\Lambda \subseteq \mathbb {R}^2$
is a choice of positively oriented
$\Lambda \subseteq \mathbb {R}^2$
is a choice of positively oriented
![]() $\mathbb {R}$
-basis
$\mathbb {R}$
-basis
![]() $(v_1,v_2)$
of
$(v_1,v_2)$
of
![]() $\mathbb {R}^2$
such that
$\mathbb {R}^2$
such that
![]() $\Lambda = \mathrm {span}_{\mathbb {Z}}(v_1,v_2)$
. The covolume of a lattice
$\Lambda = \mathrm {span}_{\mathbb {Z}}(v_1,v_2)$
. The covolume of a lattice
![]() $\Lambda := \mathrm {span}_{\mathbb {Z}}(v_1,v_2) \subseteq \mathbb {R}^2$
is defined as
$\Lambda := \mathrm {span}_{\mathbb {Z}}(v_1,v_2) \subseteq \mathbb {R}^2$
is defined as
![]() $\mathrm {covol}(\Lambda ) := |\mathrm {det}(v_1,v_2)|$
. This definition is independent of the choice of marking
$\mathrm {covol}(\Lambda ) := |\mathrm {det}(v_1,v_2)|$
. This definition is independent of the choice of marking
![]() $(v_1,v_2)$
. A lattice is said to be unimodular if it has unit covolume.
$(v_1,v_2)$
. A lattice is said to be unimodular if it has unit covolume.
Notice that the special linear group
 $$ \begin{align*} \mathrm{SL}(2,\mathbb {R}) := \left\lbrace \left( \begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right) \in \mathrm{Mat}_{2\times2}(\mathbb {R})\ \bigg\vert \ a,b,c,d \in \mathbb {R}, \thinspace ab-cd = 1 \right\rbrace \end{align*} $$
$$ \begin{align*} \mathrm{SL}(2,\mathbb {R}) := \left\lbrace \left( \begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right) \in \mathrm{Mat}_{2\times2}(\mathbb {R})\ \bigg\vert \ a,b,c,d \in \mathbb {R}, \thinspace ab-cd = 1 \right\rbrace \end{align*} $$
acts transitively on the set of unimodular lattices through its linear action on
![]() $\mathbb {R}^2$
. The stabilizer of the integer lattice
$\mathbb {R}^2$
. The stabilizer of the integer lattice
![]() $\mathbb {Z}^2 \subseteq \mathbb {R}^2$
is the group
$\mathbb {Z}^2 \subseteq \mathbb {R}^2$
is the group
![]() $\mathrm {SL}(2,\mathbb {Z}) \subseteq \mathrm {SL}(2,\mathbb {R})$
. We can thus identify the space of unimodular lattices of
$\mathrm {SL}(2,\mathbb {Z}) \subseteq \mathrm {SL}(2,\mathbb {R})$
. We can thus identify the space of unimodular lattices of
![]() $\mathbb {R}^2$
with the quotient
$\mathbb {R}^2$
with the quotient
![]() $T^1 \mathcal {M}_1 := \mathrm {SL}(2,\mathbb {R})/\mathrm {SL}(2,\mathbb {Z})$
. The corresponding identification maps the equivalence class of matrices
$T^1 \mathcal {M}_1 := \mathrm {SL}(2,\mathbb {R})/\mathrm {SL}(2,\mathbb {Z})$
. The corresponding identification maps the equivalence class of matrices
![]() $[A] \in T^1 \mathcal {M}_1$
to the lattice
$[A] \in T^1 \mathcal {M}_1$
to the lattice
![]() $A \cdot \mathbb {Z}^2 \subseteq \mathbb {R}^2$
.
$A \cdot \mathbb {Z}^2 \subseteq \mathbb {R}^2$
.
Notice that the special orthogonal group
 $$ \begin{align*} \mathrm{SO}(2) := \left\lbrace \left(\begin{array}{@{}c c@{}} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \in \mathrm{Mat}_{2 \times 2}(\mathbb {R}) \ \bigg\vert \ \theta \in [0,2\pi] \right \rbrace \end{align*} $$
$$ \begin{align*} \mathrm{SO}(2) := \left\lbrace \left(\begin{array}{@{}c c@{}} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \in \mathrm{Mat}_{2 \times 2}(\mathbb {R}) \ \bigg\vert \ \theta \in [0,2\pi] \right \rbrace \end{align*} $$
acts on the space of unimodular lattices through its linear action on
![]() $\mathbb {R}^2$
, or, equivalently, by left multiplication on
$\mathbb {R}^2$
, or, equivalently, by left multiplication on
![]() $T^1 \mathcal {M}_1$
. The corresponding quotient
$T^1 \mathcal {M}_1$
. The corresponding quotient
![]() $\mathcal {M}_1:= \mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})/\mathrm {SL}(2,\mathbb {Z})$
can thus be identified with the space of unimodular lattices of
$\mathcal {M}_1:= \mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})/\mathrm {SL}(2,\mathbb {Z})$
can thus be identified with the space of unimodular lattices of
![]() $\mathbb {R}^2$
up to rotation.
$\mathbb {R}^2$
up to rotation.
It will be convenient to consider the following alternative description of the space of unimodular lattices of
![]() $\mathbb {R}^2$
up to rotation. Denote the upper half-space by
$\mathbb {R}^2$
up to rotation. Denote the upper half-space by
The space
![]() $\mathbf {H}^2$
can be identified with the space
$\mathbf {H}^2$
can be identified with the space
![]() $\mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
of marked unimodular lattices of
$\mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
of marked unimodular lattices of
![]() $\mathbb {R}^2$
up to rotation via the map which sends
$\mathbb {R}^2$
up to rotation via the map which sends
![]() $z \in \mathbf {H}^2$
to the marked unimodular lattice
$z \in \mathbf {H}^2$
to the marked unimodular lattice
![]() $\Lambda (z) := \mathrm {span}_{\mathbb {Z}}(c_z e_1,c_z z) \subseteq \mathbb {R}^2$
, where
$\Lambda (z) := \mathrm {span}_{\mathbb {Z}}(c_z e_1,c_z z) \subseteq \mathbb {R}^2$
, where
![]() $c_z := \Im (z)^{-1/2}> 0$
; essentially, because rotations are allowed, prescribing any vector
$c_z := \Im (z)^{-1/2}> 0$
; essentially, because rotations are allowed, prescribing any vector
![]() $z \in \mathbf {H}^2$
generates an arbitrary marked unimodular lattice together with the vector
$z \in \mathbf {H}^2$
generates an arbitrary marked unimodular lattice together with the vector
![]() $(1,0) \in \mathbb {Z}^2$
after appropriately rescaling. The discrete group
$(1,0) \in \mathbb {Z}^2$
after appropriately rescaling. The discrete group
![]() $\mathrm {SL}(2,\mathbb {Z})$
acts properly discontinuously on
$\mathrm {SL}(2,\mathbb {Z})$
acts properly discontinuously on
![]() $\mathbf {H}^2$
by Möbius transformations in the following way:
$\mathbf {H}^2$
by Möbius transformations in the following way:
 $$ \begin{align*} \left(\begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right) \cdot z = \frac{az+b}{cz+d}, \quad z \in \mathbf{H}^2. \end{align*} $$
$$ \begin{align*} \left(\begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right) \cdot z = \frac{az+b}{cz+d}, \quad z \in \mathbf{H}^2. \end{align*} $$
The identification above intertwines this action with the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
by right multiplication. Thus, the quotient
$\mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
by right multiplication. Thus, the quotient
![]() $\mathcal {M}_1 := \mathbf {H}^2/\mathrm {SL}(2,\mathbb {Z})$
, commonly known as the modular curve, can be identified with the space of unimodular lattices of
$\mathcal {M}_1 := \mathbf {H}^2/\mathrm {SL}(2,\mathbb {Z})$
, commonly known as the modular curve, can be identified with the space of unimodular lattices of
![]() $\mathbb {R}^2$
up to rotation. See Figure 2 for a representation of this space using a fundamental domain of the action of
$\mathbb {R}^2$
up to rotation. See Figure 2 for a representation of this space using a fundamental domain of the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathbf {H}^2$
.
$\mathbf {H}^2$
.

Figure 2 A fundamental domain of the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathbf {H}^2$
and its quotient, the modular curve
$\mathbf {H}^2$
and its quotient, the modular curve
![]() $\mathcal {M}_1$
(colour online).
$\mathcal {M}_1$
(colour online).
Consider the Lebesgue class measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbf {H}^2$
given in coordinates
$\mathbf {H}^2$
given in coordinates
![]() $z = x + iy$
by
$z = x + iy$
by
Alternatively, after identifying
![]() $\mathbf {H}^2 = \mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
, the measure
$\mathbf {H}^2 = \mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
, the measure
![]() $\mu $
is obtained by integrating the
$\mu $
is obtained by integrating the
![]() $\mathrm {SO}(2)$
-direction of the Haar measure on
$\mathrm {SO}(2)$
-direction of the Haar measure on
![]() $\mathrm {SL}(2,\mathbb {R})$
. A direct computation shows that
$\mathrm {SL}(2,\mathbb {R})$
. A direct computation shows that
![]() $\mu $
is preserved by the action of
$\mu $
is preserved by the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathbf {H}^2$
; see Exercise 2.9. Denote by
$\mathbf {H}^2$
; see Exercise 2.9. Denote by
![]() $\smash {\widehat {\mu }}$
the local pushforward of
$\smash {\widehat {\mu }}$
the local pushforward of
![]() $\mu $
to the quotient
$\mu $
to the quotient
![]() $\mathcal {M}_1 := \mathbf {H}^2/\mathrm {SL}(2,\mathbb {Z})$
. More explicitly, this is the measure on
$\mathcal {M}_1 := \mathbf {H}^2/\mathrm {SL}(2,\mathbb {Z})$
. More explicitly, this is the measure on
![]() $\mathcal {M}_1$
obtained by restricting
$\mathcal {M}_1$
obtained by restricting
![]() $\mu $
to the fundamental domain of the action of
$\mu $
to the fundamental domain of the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathbf {H}^2$
in Figure 2. Local pushforwards of measures will be discussed in more detail in §3 following an approach independent of fundamental domains. Nevertheless, the explicit fundamental domain in Figure 2 is useful for computing the total mass
$\mathbf {H}^2$
in Figure 2. Local pushforwards of measures will be discussed in more detail in §3 following an approach independent of fundamental domains. Nevertheless, the explicit fundamental domain in Figure 2 is useful for computing the total mass
![]() $\smash {\widehat {\mu }(\mathcal {M}_1)}$
, as suggested in the following exercise.
$\smash {\widehat {\mu }(\mathcal {M}_1)}$
, as suggested in the following exercise.
Exercise 2.9. Using change of variables, show that the measure
![]() $\mu $
is preserved by the action of
$\mu $
is preserved by the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathbf {H}^2$
. Using Figure 2, show that
$\mathbf {H}^2$
. Using Figure 2, show that
![]() $\smash {\widehat {\mu }(\mathcal {M}_1)} = \pi /3$
.
$\smash {\widehat {\mu }(\mathcal {M}_1)} = \pi /3$
.
2.9 Averaging over the space of unimodular lattices
Let
![]() $\Lambda \in \mathcal {M}_1$
be a unimodular lattice of
$\Lambda \in \mathcal {M}_1$
be a unimodular lattice of
![]() $\mathbb {R}^2$
. A vector
$\mathbb {R}^2$
. A vector
![]() $v \in \Lambda $
is said to be primitive if it cannot be written as a non-negative integer multiple of another vector of
$v \in \Lambda $
is said to be primitive if it cannot be written as a non-negative integer multiple of another vector of
![]() $\Lambda $
. Denote by
$\Lambda $
. Denote by
![]() $\Lambda _{\mathrm {prim}} \subseteq \Lambda $
the subset of all primitive vectors of
$\Lambda _{\mathrm {prim}} \subseteq \Lambda $
the subset of all primitive vectors of
![]() $\Lambda $
. Recall that
$\Lambda $
. Recall that
![]() $\| \cdot \|$
denotes the Euclidean norm of
$\| \cdot \|$
denotes the Euclidean norm of
![]() $\mathbb {R}^2$
. For every
$\mathbb {R}^2$
. For every
![]() $L> 0$
, we consider the counting function
$L> 0$
, we consider the counting function
As one might already expect after considering the case of the integer lattice
![]() $\mathbb {Z}^2 \subseteq \mathbb {R}^2$
, explicitly describing
$\mathbb {Z}^2 \subseteq \mathbb {R}^2$
, explicitly describing
![]() $p(\Lambda ,L)$
for a given unimodular lattice
$p(\Lambda ,L)$
for a given unimodular lattice
![]() $\Lambda \in \mathcal {M}_1$
as a function of L is a particularly hard problem. Nevertheless, and perhaps surprisingly, the average
$\Lambda \in \mathcal {M}_1$
as a function of L is a particularly hard problem. Nevertheless, and perhaps surprisingly, the average
 $$ \begin{align*} \int_{\mathcal{M}_1} p(\Lambda,L) \thinspace d\widehat{\mu}(\Lambda) \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_1} p(\Lambda,L) \thinspace d\widehat{\mu}(\Lambda) \end{align*} $$
can be computed explicitly, as the next result shows.
Proposition 2.10. The following integration formula holds:
 $$ \begin{align*} \int_{\mathcal{M}_1} p(\Lambda,L) \thinspace d\widehat{\mu}(\Lambda) = 2 \cdot L^2. \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_1} p(\Lambda,L) \thinspace d\widehat{\mu}(\Lambda) = 2 \cdot L^2. \end{align*} $$
In §4, we will prove this result using a general local change of variables formula; see Exercise 4.3. From a more classical point of view, Proposition 2.10 is a consequence of Siegel’s famous integration formulas over
![]() $\mathcal {M}_1$
[Reference SiegelSie45].
$\mathcal {M}_1$
[Reference SiegelSie45].
To prove Theorem 2.1, we will need a more uniform control on the integrability of the counting functions
![]() $p(\Lambda ,L)$
as
$p(\Lambda ,L)$
as
![]() $L \to \infty $
. To this end, we consider the function
$L \to \infty $
. To this end, we consider the function
![]() $u \colon \mathcal {M}_1 \to \mathbb {R}$
given by
$u \colon \mathcal {M}_1 \to \mathbb {R}$
given by
Exercise 2.11. Show there exists a constant
![]() $C> 0$
such that for every
$C> 0$
such that for every
![]() $\Lambda \in \mathcal {M}_1$
and every
$\Lambda \in \mathcal {M}_1$
and every
![]() $L> 0$
,
$L> 0$
,
Additionally, show that the function
![]() $u \colon \mathcal {M}_1 \to \mathbb {R}$
is integrable with respect to the measure
$u \colon \mathcal {M}_1 \to \mathbb {R}$
is integrable with respect to the measure
![]() $\widehat {\mu }$
, that is,
$\widehat {\mu }$
, that is,
 $$ \begin{align*} \int_{\mathcal{M}_1} u(\Lambda) \thinspace d\widehat{\mu}(\Lambda) < \infty. \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_1} u(\Lambda) \thinspace d\widehat{\mu}(\Lambda) < \infty. \end{align*} $$
2.10 Convergence and compactness
Before proceeding with the proof of Theorem 2.1, let us discuss a couple of basic convergence and compactness criteria. To prove the sequence of counting measure
![]() $(\nu ^{\mathrm {prim}}_L)_{L> 0}$
on
$(\nu ^{\mathrm {prim}}_L)_{L> 0}$
on
![]() $\mathbb {R}^2$
converges in the weak-
$\mathbb {R}^2$
converges in the weak-
![]() $\star $
topology, we will use the following convergence criterion.
$\star $
topology, we will use the following convergence criterion.
Exercise 2.12. Let X be a metric space. Show that a sequence
![]() $(x_L)_{L>0}$
in X converges to
$(x_L)_{L>0}$
in X converges to
![]() $x \in X$
if and only if every subsequence of
$x \in X$
if and only if every subsequence of
![]() $(x_L)_{L>0}$
has a subsubsequence converging to x.
$(x_L)_{L>0}$
has a subsubsequence converging to x.
The following compactness criterion for the weak-
![]() $\star $
topology serves as a convenient tool for extracting convergent subsequences of locally finite measures on metric spaces. This result is a consequence of the well-known Banach–Alaoglu theorem in functional analysis.
$\star $
topology serves as a convenient tool for extracting convergent subsequences of locally finite measures on metric spaces. This result is a consequence of the well-known Banach–Alaoglu theorem in functional analysis.
Theorem 2.13. Let X be a metric space and
![]() $(\mu _n)_{n \in \mathbb{N}}$
be a sequence of locally finite measures on X. Suppose that the sequence
$(\mu _n)_{n \in \mathbb{N}}$
be a sequence of locally finite measures on X. Suppose that the sequence
![]() $(\mu _n(K))_{n \in \mathbb{N}}$
is bounded for every
$(\mu _n(K))_{n \in \mathbb{N}}$
is bounded for every
![]() $K \subseteq X$
compact. Then, the sequence
$K \subseteq X$
compact. Then, the sequence
![]() $(\mu _n)_{n \in \mathbb{N}}$
has a subsequence converging in the weak-
$(\mu _n)_{n \in \mathbb{N}}$
has a subsequence converging in the weak-
![]() $\star $
topology to a locally finite measure on X.
$\star $
topology to a locally finite measure on X.
2.11 Equidistribution of primitive integer points
We are finally ready to prove that the sequence of counting measure
![]() $\smash {(\nu ^{\mathrm {prim}}_L)_{L> 0}}$
on
$\smash {(\nu ^{\mathrm {prim}}_L)_{L> 0}}$
on
![]() $\mathbb {R}^2$
converges in the weak-
$\mathbb {R}^2$
converges in the weak-
![]() $\star $
topology to a constant multiple of the Lebesgue measure
$\star $
topology to a constant multiple of the Lebesgue measure
![]() $\nu $
. We will later deduce Theorem 2.1 directly from this result.
$\nu $
. We will later deduce Theorem 2.1 directly from this result.
Theorem 2.14. With respect to the weak-
![]() $\star $
topology for measures on
$\star $
topology for measures on
![]() $\mathbb {R}^2$
,
$\mathbb {R}^2$
,
Proof. By Exercise 2.12 applied to the space of regular measures on
![]() $\mathbb {R}^2$
with the weak-
$\mathbb {R}^2$
with the weak-
![]() $\star $
topology, it is enough to show every subsequence of
$\star $
topology, it is enough to show every subsequence of
![]() $\smash {(\nu ^{\mathrm {prim}}_L)_{L> 0}}$
has a subsubsequence converging to
$\smash {(\nu ^{\mathrm {prim}}_L)_{L> 0}}$
has a subsubsequence converging to
![]() $(6/\pi ^2) \cdot \nu $
in the weak-
$(6/\pi ^2) \cdot \nu $
in the weak-
![]() $\star $
topology. Theorem 2.13 and the bound in equation (2.9) ensure that every subsequence of
$\star $
topology. Theorem 2.13 and the bound in equation (2.9) ensure that every subsequence of
![]() $\smash {(\nu ^{\mathrm {prim}}_L)_{L> 0}}$
has a subsubsequence
$\smash {(\nu ^{\mathrm {prim}}_L)_{L> 0}}$
has a subsubsequence
![]() $\smash {(\nu ^{\mathrm {prim}}_{L_k})_{k \in \mathbb{N}}}$
converging in the weak-
$\smash {(\nu ^{\mathrm {prim}}_{L_k})_{k \in \mathbb{N}}}$
converging in the weak-
![]() $\star $
topology to a locally finite measure
$\star $
topology to a locally finite measure
![]() $\nu ^{\mathrm {prim}}$
on
$\nu ^{\mathrm {prim}}$
on
![]() $\mathbb {R}^2$
. By Proposition 2.8, it must be the case that
$\mathbb {R}^2$
. By Proposition 2.8, it must be the case that
![]() $\nu ^{\mathrm {prim}} = c \cdot \nu $
for some constant
$\nu ^{\mathrm {prim}} = c \cdot \nu $
for some constant
![]() $c \geq 0$
. It is enough then to show that
$c \geq 0$
. It is enough then to show that
![]() $c = 6/\pi ^2$
, independent of the subsubsequence considered. To prove this identity holds, we compute the following limit in two different ways:
$c = 6/\pi ^2$
, independent of the subsubsequence considered. To prove this identity holds, we compute the following limit in two different ways:
 $$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_1} \frac{p(\Lambda,L_k)}{L_k^2} \thinspace d\widehat{\mu}(\Lambda). \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_1} \frac{p(\Lambda,L_k)}{L_k^2} \thinspace d\widehat{\mu}(\Lambda). \end{align*} $$
The first computation is immediate. Directly from Proposition 2.10, we deduce
 $$ \begin{align} \lim_{k \to \infty} \int_{\mathcal{M}_1} \frac{p(\Lambda,L_k)}{L_k^2} \thinspace d\widehat{\mu}(\Lambda) = 2. \end{align} $$
$$ \begin{align} \lim_{k \to \infty} \int_{\mathcal{M}_1} \frac{p(\Lambda,L_k)}{L_k^2} \thinspace d\widehat{\mu}(\Lambda) = 2. \end{align} $$
The second computation requires more work. For every matrix
![]() $A \in \mathrm {SL}(2,\mathbb {R})$
, consider the subset
$A \in \mathrm {SL}(2,\mathbb {R})$
, consider the subset
Notice that
![]() $\nu (B_A) = 1$
for every
$\nu (B_A) = 1$
for every
![]() $A \in \mathrm {SL}(2,\mathbb {R})$
. Notice also that for every unimodular lattice
$A \in \mathrm {SL}(2,\mathbb {R})$
. Notice also that for every unimodular lattice
![]() $\Lambda := A \cdot \mathbb {Z}^2 \in \mathcal {M}_1$
with
$\Lambda := A \cdot \mathbb {Z}^2 \in \mathcal {M}_1$
with
![]() $A \in \mathrm {SL}(2,\mathbb {R})$
, and every
$A \in \mathrm {SL}(2,\mathbb {R})$
, and every
![]() $k \in \mathbb{N}$
,
$k \in \mathbb{N}$
,
 $$ \begin{align*} \frac{p(\Lambda,L_k)}{L_k^2} = \smash{\nu_{L_k}^{\mathrm{prim}}}(B_A). \end{align*} $$
$$ \begin{align*} \frac{p(\Lambda,L_k)}{L_k^2} = \smash{\nu_{L_k}^{\mathrm{prim}}}(B_A). \end{align*} $$
In this setting, as
![]() $\lim _{k \to \infty } \smash {\nu ^{\mathrm {prim}}_{L_k}} = c \cdot \nu $
in the weak-
$\lim _{k \to \infty } \smash {\nu ^{\mathrm {prim}}_{L_k}} = c \cdot \nu $
in the weak-
![]() $\star $
topology, Theorem 2.6 ensures that
$\star $
topology, Theorem 2.6 ensures that
 $$ \begin{align*} \lim_{k \to \infty} \frac{p(\Lambda,L_k)}{L_k^2} = \lim_{k \to \infty} \smash{\nu^{\mathrm{prim}}_{L_k}}(B_A) = c \cdot \nu(B_A) = c \cdot \pi. \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty} \frac{p(\Lambda,L_k)}{L_k^2} = \lim_{k \to \infty} \smash{\nu^{\mathrm{prim}}_{L_k}}(B_A) = c \cdot \nu(B_A) = c \cdot \pi. \end{align*} $$
Exercise 2.11 now allows us to use the dominate convergence theorem to deduce
 $$ \begin{align} \lim_{k \to \infty} \int_{\mathcal{M}_1} \frac{p(\Lambda,L_k)}{L_k^2} \thinspace d\widehat{\mu}(\Lambda) = c \cdot \frac{\pi^2}{3}. \end{align} $$
$$ \begin{align} \lim_{k \to \infty} \int_{\mathcal{M}_1} \frac{p(\Lambda,L_k)}{L_k^2} \thinspace d\widehat{\mu}(\Lambda) = c \cdot \frac{\pi^2}{3}. \end{align} $$
Putting together equations (2.15) and (2.16), we obtain
Solving for c, we conclude
![]() $c = 6/\pi ^2$
, and thus finish the proof.
$c = 6/\pi ^2$
, and thus finish the proof.
Exercise 2.15. Recall the definition of the sequence of counting measures
![]() $(\nu _{L})_{L> 0}$
on
$(\nu _{L})_{L> 0}$
on
![]() $\mathbb {R}^2$
in equation (2.2). Using the methods introduced in the proof of Theorem 2.14, show that equation (2.3) holds, that is, show that with respect to the weak-
$\mathbb {R}^2$
in equation (2.2). Using the methods introduced in the proof of Theorem 2.14, show that equation (2.3) holds, that is, show that with respect to the weak-
![]() $\star $
topology for measures on
$\star $
topology for measures on
![]() $\mathbb {R}^2$
,
$\mathbb {R}^2$
,
2.12 Counting primitive integer points
We are now ready to prove Theorem 2.1, the main result of this section. Let us restate this theorem in the following equivalent way.
Theorem 2.16. The following asymptotic estimate holds:
Proof. Recall that if
![]() $B \subseteq \mathbb {R}^2$
is the Euclidean unit ball centered at the origin, then, for every
$B \subseteq \mathbb {R}^2$
is the Euclidean unit ball centered at the origin, then, for every
![]() $L> 0$
,
$L> 0$
,
Using Theorems 2.14 and 2.6, we conclude
Exercise 2.17. Using Theorem 2.14, show that for every unimodular lattice
![]() $\Lambda \in \mathcal {M}_1$
,
$\Lambda \in \mathcal {M}_1$
,
Remark 2.18. Comparing Exercise 2.17 to Theorem 1.1, one can see that, very different to the case of unimodular lattices, the leading constant in Mirzakhani’s counting formula does depend on the underlying hyperbolic surface. Later, in Exercises 5.13 and 5.14, a more explicit description of this constant will be provided.
3 Hyperbolic surfaces, Teichmüller spaces, and simple closed curves
3.1 Outline of this section
In this section, we cover the background material needed to understand the proof of Theorem 1.1. The focus will be in developing geometric intuition rather than on giving complete proofs. Unless otherwise stated, all surfaces considered will be connected and orientable. Two excellent references for the topics that will be covered in this section are [Reference Farb and MargalitFM12, Reference MartelliMar23].
3.2 The hyperbolic plane
By definition, the hyperbolic plane
![]() $\mathbf {H}^2$
is the unique, up to isometry, two-dimensional simply connected Riemannian manifold of constant sectional curvature
$\mathbf {H}^2$
is the unique, up to isometry, two-dimensional simply connected Riemannian manifold of constant sectional curvature
![]() $-1$
. Recall that the hyperbolic plane can be modeled on the upper half space
$-1$
. Recall that the hyperbolic plane can be modeled on the upper half space
![]() $\{z \in \mathbf {C} \mid \Im (z)> 0\}$
by endowing it with the Riemannian metric
$\{z \in \mathbf {C} \mid \Im (z)> 0\}$
by endowing it with the Riemannian metric
 $$ \begin{align*} g := \frac{dx^2 + dy^2}{y^2}. \end{align*} $$
$$ \begin{align*} g := \frac{dx^2 + dy^2}{y^2}. \end{align*} $$
The geodesics of this metric are the lines and half circles of the upper half space perpendicular to the the real axis
![]() $\mathbb {R} \subseteq \mathbf {C}$
. See Figure 3. The orientation-preserving isometries of this metric can be identified with the group
$\mathbb {R} \subseteq \mathbf {C}$
. See Figure 3. The orientation-preserving isometries of this metric can be identified with the group
![]() $\mathrm {PSL}(2,\mathbb {R}) = \mathrm {SL}(2,\mathbb {R})/\{\pm \mathrm {Id}\}$
acting on
$\mathrm {PSL}(2,\mathbb {R}) = \mathrm {SL}(2,\mathbb {R})/\{\pm \mathrm {Id}\}$
acting on
![]() $\mathbf {H}^2$
by Möbius transformations:
$\mathbf {H}^2$
by Möbius transformations:
 $$ \begin{align*} \left( \begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right).z := \frac{az +b}{cz+d} \quad \text{for all } z \in \mathbf{H}. \end{align*} $$
$$ \begin{align*} \left( \begin{array}{@{}c c@{}} a & b \\ c & d \end{array}\right).z := \frac{az +b}{cz+d} \quad \text{for all } z \in \mathbf{H}. \end{align*} $$

Figure 3 The geodesics of the hyperbolic plane.
This group acts simply transitively on the unit tangent bundle of
![]() $\mathbf {H}^2$
; through this action, one can realize
$\mathbf {H}^2$
; through this action, one can realize
![]() $\mathbf {H}^2$
as the symmetric space
$\mathbf {H}^2$
as the symmetric space
![]() $\mathrm {SO}(2) \backslash \mathrm {SL}(2,\mathbb {R})$
. Such a large isometry group should hint at a rigid geometry: it becomes hard to distinguish objects up to isometry. The next exercise is an important manifestation of this idea.
$\mathrm {SO}(2) \backslash \mathrm {SL}(2,\mathbb {R})$
. Such a large isometry group should hint at a rigid geometry: it becomes hard to distinguish objects up to isometry. The next exercise is an important manifestation of this idea.
Exercise 3.1. Show that for every
![]() $(a,b,c) \in (\mathbb {R}_+)^3$
, there exists a unique, up to isometry, hyperbolic right-angled hexagon with alternating edge lengths
$(a,b,c) \in (\mathbb {R}_+)^3$
, there exists a unique, up to isometry, hyperbolic right-angled hexagon with alternating edge lengths
![]() $(a,b,c)$
. Hint: Consider a configuration as in Figure 4 and study how the length
$(a,b,c)$
. Hint: Consider a configuration as in Figure 4 and study how the length
![]() $c(y)$
varies as the parameter y varies.
$c(y)$
varies as the parameter y varies.

Figure 4 Right-angled hyperbolic hexagons are rigid.
Despite Exercise 3.1, hyperbolic geometry in dimension
![]() $2$
remains quite flexible, as we will see below. In higher dimensions, the picture becomes incredibly rigid; curious readers are invited to investigate Mostow’s rigidity theorem [Reference MostowMos68].
$2$
remains quite flexible, as we will see below. In higher dimensions, the picture becomes incredibly rigid; curious readers are invited to investigate Mostow’s rigidity theorem [Reference MostowMos68].
3.3 Hyperbolic surfaces
A hyperbolic surface is a surface whose geometry is locally modeled on
![]() $\mathbf {H}^2$
. More concretely, a hyperbolic surface X is a surface endowed with an atlas of charts to
$\mathbf {H}^2$
. More concretely, a hyperbolic surface X is a surface endowed with an atlas of charts to
![]() $\mathbf {H}^2$
whose transition functions are restrictions of isometries of
$\mathbf {H}^2$
whose transition functions are restrictions of isometries of
![]() $\mathbf {H}^2$
. Pulling back the metric of
$\mathbf {H}^2$
. Pulling back the metric of
![]() $\mathbf {H}^2$
via these charts yields a metric of constant curvature equal to
$\mathbf {H}^2$
via these charts yields a metric of constant curvature equal to
![]() $-1$
on X. A geodesic of X is a geodesic of this metric. Equivalently, a geodesic of X is a curve which is mapped to geodesics of
$-1$
on X. A geodesic of X is a geodesic of this metric. Equivalently, a geodesic of X is a curve which is mapped to geodesics of
![]() $\mathbf {H}^2$
via local charts. Every closed curve on X can be tightened, that is, homotoped, to a unique geodesic representative.
$\mathbf {H}^2$
via local charts. Every closed curve on X can be tightened, that is, homotoped, to a unique geodesic representative.
We will not spend much time discussing the many interesting features of hyperbolic surfaces, but let us highlight one fact that is very useful to keep in mind for the sake of geometric intuition. The following fact is known as the collar lemma: every simple closed geodesic on a hyperbolic surface has a collar, that is, an embedded annular neighborhood, whose width goes to infinity as the length of the geodesic goes to zero. See Figure 5. For a more precise version of this fact, see Lemma 5.7.

Figure 5 The collar lemma (colour online).
3.4 Teichmüller space
All hyperbolic surfaces of a given genus fit together nicely into a moduli space. To keep track of how any pair of hyperbolic surfaces looks with respect to each other, we will record more information than just their position in moduli space. This leads us to introduce Teichmüller spaces. We will later see how to recover moduli spaces as quotients of Teichmüller spaces.
Throughout the rest of this survey, we use the words ‘homotopy’ and ‘isotopy’ interchangeably. This does not pose an issue because we are working in dimension 2; see [Reference Farb and MargalitFM12, Ch. 1] for a detailed discussion on this highly non-trivial matter.
For the rest of this lecture, we fix an integer
![]() $g \geq 2$
and a connected, oriented, closed surface
$g \geq 2$
and a connected, oriented, closed surface
![]() $S_g$
of genus g. The Teichmüller space
$S_g$
of genus g. The Teichmüller space
![]() $\mathcal {T}_{g}$
of marked hyperbolic structures on
$\mathcal {T}_{g}$
of marked hyperbolic structures on
![]() $S_g$
is the space of all pairs
$S_g$
is the space of all pairs
![]() $(X,\varphi )$
, where X is an oriented hyperbolic surface and
$(X,\varphi )$
, where X is an oriented hyperbolic surface and
![]() $\varphi \colon S_g \to X$
is an orientation-preserving homeomorphism, modulo the equivalence relation
$\varphi \colon S_g \to X$
is an orientation-preserving homeomorphism, modulo the equivalence relation
![]() $(X_1,\varphi _1) \sim (X_2,\varphi _2)$
if and only if there exists an orientation-preserving isometry
$(X_1,\varphi _1) \sim (X_2,\varphi _2)$
if and only if there exists an orientation-preserving isometry
![]() $I \colon X_1 \to X_2$
isotopic to
$I \colon X_1 \to X_2$
isotopic to
![]() $\varphi _2 \circ \varphi _1^{-1}$
. In most situations, we will omit the marking of a point
$\varphi _2 \circ \varphi _1^{-1}$
. In most situations, we will omit the marking of a point
![]() $(X,\varphi ) \in \mathcal {T}_g$
and denote it simply by
$(X,\varphi ) \in \mathcal {T}_g$
and denote it simply by
![]() $X \in \mathcal {T}_g$
.
$X \in \mathcal {T}_g$
.
Roughly speaking, a point in Teichmüller space does not only keep track of a hyperbolic structure on
![]() $S_g$
but also of how
$S_g$
but also of how
![]() $S_g$
is ‘wearing’ that hyperbolic structure. This allows us to communicate marked hyperbolic structures on
$S_g$
is ‘wearing’ that hyperbolic structure. This allows us to communicate marked hyperbolic structures on
![]() $S_g$
in a very explicit way. For instance, given a marked hyperbolic structure
$S_g$
in a very explicit way. For instance, given a marked hyperbolic structure
![]() $(X,\varphi ) \in \mathcal {T}_g$
, any parameterized closed curve
$(X,\varphi ) \in \mathcal {T}_g$
, any parameterized closed curve
![]() $\gamma $
on
$\gamma $
on
![]() $S_g$
can be canonically identified with the closed geodesic obtained by tightening the closed curve
$S_g$
can be canonically identified with the closed geodesic obtained by tightening the closed curve
![]() $\varphi (\gamma )$
on X to its unique geodesics representative. We denote the length of this representative by
$\varphi (\gamma )$
on X to its unique geodesics representative. We denote the length of this representative by
![]() $\ell _\gamma (X)$
.
$\ell _\gamma (X)$
.
3.5 The mapping class group
The mapping class group of
![]() $S_g$
, denoted
$S_g$
, denoted
![]() $\mathrm {Mod}_g$
, is the group of orientation-preserving homeomorphisms of
$\mathrm {Mod}_g$
, is the group of orientation-preserving homeomorphisms of
![]() $S_g$
up to homotopy. More explicitly,
$S_g$
up to homotopy. More explicitly,
This group acts naturally on
![]() $\mathcal {T}_g$
by changing the markings: for every
$\mathcal {T}_g$
by changing the markings: for every
![]() $(X,\varphi ) \in \mathcal {T}_g$
and every
$(X,\varphi ) \in \mathcal {T}_g$
and every
![]() $\phi \in \mathrm {Mod}_g$
,
$\phi \in \mathrm {Mod}_g$
,
We think of
![]() $\mathrm {Mod}_g$
acting on
$\mathrm {Mod}_g$
acting on
![]() ${\mathcal {T}_g}$
as an analog of
${\mathcal {T}_g}$
as an analog of
![]() $\mathrm {SL}(2,\mathbb {Z})$
acting on
$\mathrm {SL}(2,\mathbb {Z})$
acting on
![]() $\mathbf {H}^2$
.
$\mathbf {H}^2$
.
Exercise 3.2. Let
![]() $(X,\varphi ) \in \mathcal {T}_g$
be a marked hyperbolic structure on
$(X,\varphi ) \in \mathcal {T}_g$
be a marked hyperbolic structure on
![]() $S_g$
. Show there exists a natural one-to-one correspondence between the
$S_g$
. Show there exists a natural one-to-one correspondence between the
![]() $\mathrm {Mod}_g$
stabilizer of
$\mathrm {Mod}_g$
stabilizer of
![]() $(X,\varphi )$
and the set of isometries of X.
$(X,\varphi )$
and the set of isometries of X.
A particularly important family of mapping classes are Dehn twists. Given a simple closed curve
![]() $\gamma $
on
$\gamma $
on
![]() $S_g$
, the Dehn twist
$S_g$
, the Dehn twist
![]() $T_\gamma $
of
$T_\gamma $
of
![]() $S_g$
along
$S_g$
along
![]() $\gamma $
is the mapping class which leaves the surface
$\gamma $
is the mapping class which leaves the surface
![]() $S_g$
untouched except for an embedded annular neighborhood of
$S_g$
untouched except for an embedded annular neighborhood of
![]() $\gamma $
which gets twisted to the right, with respect to the orientation of
$\gamma $
which gets twisted to the right, with respect to the orientation of
![]() $S_g$
, by a full rotation. See Figure 6.
$S_g$
, by a full rotation. See Figure 6.

Figure 6 Dehn twist in an annular neighborhood of a simple closed curve
![]() $\gamma $
(in green) (colour online).
$\gamma $
(in green) (colour online).
3.6 Moduli space of hyperbolic surfaces
As
![]() $\mathrm {Mod}_g$
acts on
$\mathrm {Mod}_g$
acts on
![]() $\mathcal {T}_g$
by changing the markings, one should expect that, if one quotients
$\mathcal {T}_g$
by changing the markings, one should expect that, if one quotients
![]() $\mathcal {T}_g$
by this action, one should get a space grouping together all (unmarked) hyperbolic surfaces of genus g. It turns out that
$\mathcal {T}_g$
by this action, one should get a space grouping together all (unmarked) hyperbolic surfaces of genus g. It turns out that
![]() $\mathrm {Mod}_g$
acts on
$\mathrm {Mod}_g$
acts on
![]() $\mathcal {T}_g$
properly discontinuously and thus the corresponding quotient behaves nicely. The quotient
$\mathcal {T}_g$
properly discontinuously and thus the corresponding quotient behaves nicely. The quotient
![]() $\mathcal {M}_g := \mathcal {T}_g / {\mathrm {Mod}_g}$
is the moduli space of genus g hyperbolic surfaces. By uniformization, this space can be canonically identified with the moduli space of genus g Riemann surfaces you might have seen in algebraic geometry.
$\mathcal {M}_g := \mathcal {T}_g / {\mathrm {Mod}_g}$
is the moduli space of genus g hyperbolic surfaces. By uniformization, this space can be canonically identified with the moduli space of genus g Riemann surfaces you might have seen in algebraic geometry.
3.7 Fenchel–Nielsen coordinates
Notice that any orientable topological surface of genus
![]() $g \geq 2$
can be constructed by gluing
$g \geq 2$
can be constructed by gluing
![]() $2g-2$
pairs of pants, that is, spheres with three boundary components, along their boundaries. See Figure 7 for an example. A similar construction can also be considered for hyperbolic surfaces. Indeed, cutting an orientable hyperbolic surface X of genus
$2g-2$
pairs of pants, that is, spheres with three boundary components, along their boundaries. See Figure 7 for an example. A similar construction can also be considered for hyperbolic surfaces. Indeed, cutting an orientable hyperbolic surface X of genus
![]() $g \geq 2$
along any collection of
$g \geq 2$
along any collection of
![]() $3g-3$
disjoint simple closed geodesics yields
$3g-3$
disjoint simple closed geodesics yields
![]() $2g-2$
hyperbolic pairs of pants with geodesic boundary components. This class of pairs of pants is very rigid, as the following exercise shows.
$2g-2$
hyperbolic pairs of pants with geodesic boundary components. This class of pairs of pants is very rigid, as the following exercise shows.
Exercise 3.3. Show that, for every
![]() $a,b,c \in \mathbb {R}_+$
, there exists a unique, up to isometry, hyperbolic pair of pants with geodesic boundary components of lengths
$a,b,c \in \mathbb {R}_+$
, there exists a unique, up to isometry, hyperbolic pair of pants with geodesic boundary components of lengths
![]() $a,b,c$
. Hint: Cutting a hyperbolic pair of pants with geodesic boundary components along the orthogeodesics joining its boundary components yields a pair of isometric hyperbolic right-angled hexagons. See Figure 8.
$a,b,c$
. Hint: Cutting a hyperbolic pair of pants with geodesic boundary components along the orthogeodesics joining its boundary components yields a pair of isometric hyperbolic right-angled hexagons. See Figure 8.

Figure 7 Pair of pants decomposition of a genus
![]() $2$
surface (colour online).
$2$
surface (colour online).

Figure 8 Cutting a hyperbolic pair of pants into isometric right-angled hexagons (colour online).
By Exercise 3.3, the hyperbolic pairs of pants obtained by cutting an orientable hyperbolic surface X of genus
![]() $g \geq 2$
along a maximal collection of disjoint simple closed geodesics are determined, up to isometry, by the lengths of the geodesics one cuts along. Gluing back these pairs of pants following the same original pattern allows us to recover X. One needs to be careful at this point as there are several ways in which one can glue back these pants along their cuffs. Indeed, for each geodesic one cutted X along, there is a full circle worth of different twists with which one can glue back the adjacent pairs of pants. If one is interested in marked hyperbolic surfaces rather than just hyperbolic surfaces, there is actually a full line worth of different twists one can glue with respect to.
$g \geq 2$
along a maximal collection of disjoint simple closed geodesics are determined, up to isometry, by the lengths of the geodesics one cuts along. Gluing back these pairs of pants following the same original pattern allows us to recover X. One needs to be careful at this point as there are several ways in which one can glue back these pants along their cuffs. Indeed, for each geodesic one cutted X along, there is a full circle worth of different twists with which one can glue back the adjacent pairs of pants. If one is interested in marked hyperbolic surfaces rather than just hyperbolic surfaces, there is actually a full line worth of different twists one can glue with respect to.
More concretely, one can deform (marked) oriented hyperbolic surfaces using the following operation: given a (marked) oriented hyperbolic surface X, a simple closed geodesic
![]() $\gamma $
on X, and
$\gamma $
on X, and
![]() $t \in \mathbb {R}$
, cut X along
$t \in \mathbb {R}$
, cut X along
![]() $\gamma $
and glue the resulting surface back along
$\gamma $
and glue the resulting surface back along
![]() $\gamma $
with a twist of t units of hyperbolic length to the right with respect to the orientation of X. See Figure 9. This operation is known as a Fenchel–Nielsen twist. Given a simple closed curve
$\gamma $
with a twist of t units of hyperbolic length to the right with respect to the orientation of X. See Figure 9. This operation is known as a Fenchel–Nielsen twist. Given a simple closed curve
![]() $\gamma $
on
$\gamma $
on
![]() $S_g$
and a marked hyperbolic structure on
$S_g$
and a marked hyperbolic structure on
![]() $X \in \mathcal {T}_g$
, the point
$X \in \mathcal {T}_g$
, the point
![]() $T_\gamma .X \in \mathcal {T}_g$
is equal to the marked hyperbolic structure obtained by doing a Fenchel–Nielsen twist of parameter
$T_\gamma .X \in \mathcal {T}_g$
is equal to the marked hyperbolic structure obtained by doing a Fenchel–Nielsen twist of parameter
![]() $t = \ell _{\gamma }(X)$
along the unique geodesic representative of
$t = \ell _{\gamma }(X)$
along the unique geodesic representative of
![]() $\gamma $
on X.
$\gamma $
on X.

Figure 9 Fenchel–Nielsen twist along a simple closed curve (in red) (colour online).
The discussion above leads us to introduce Fenchel–Nielsen coordinates. A pair of pants decomposition of
![]() $S_g$
is a maximal collection of disjoint simple closed curves on
$S_g$
is a maximal collection of disjoint simple closed curves on
![]() $S_g$
. Fix a pair of pants decomposition
$S_g$
. Fix a pair of pants decomposition
![]() $\mathcal {P} := \smash {(\gamma _i)_{i=1}^{3g-3}}$
of
$\mathcal {P} := \smash {(\gamma _i)_{i=1}^{3g-3}}$
of
![]() $S_g$
. Given a marked hyperbolic structure
$S_g$
. Given a marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
, for every
$X \in \mathcal {T}_g$
, for every
![]() $i \in \{1,\ldots ,3g-3\}$
, denote
$i \in \{1,\ldots ,3g-3\}$
, denote
![]() $\ell _i(X) := \ell _{\gamma _i}(X)$
and let
$\ell _i(X) := \ell _{\gamma _i}(X)$
and let
![]() $\tau _i(X)$
be the twist of X at the geodesic representative of
$\tau _i(X)$
be the twist of X at the geodesic representative of
![]() $\gamma _i$
. Defining what it means to have zero twist is a rather technical issue which we avoid in this survey; the interested reader is invited to consult [Reference Farb and MargalitFM12, Ch. 10]. The parameters
$\gamma _i$
. Defining what it means to have zero twist is a rather technical issue which we avoid in this survey; the interested reader is invited to consult [Reference Farb and MargalitFM12, Ch. 10]. The parameters
![]() $(\ell _i,\tau _i)_{i=1}^{3g-3} \in \smash {(\mathbb {R}_+ \times \mathbb {R})^{3g-3}}$
provide global coordinates for
$(\ell _i,\tau _i)_{i=1}^{3g-3} \in \smash {(\mathbb {R}_+ \times \mathbb {R})^{3g-3}}$
provide global coordinates for
![]() $\mathcal {T}_g$
known as Fenchel–Nielsen coordinates. In particular,
$\mathcal {T}_g$
known as Fenchel–Nielsen coordinates. In particular,
![]() $\mathcal {T}_g$
is homeomorphic to an open ball of dimension
$\mathcal {T}_g$
is homeomorphic to an open ball of dimension
![]() $6g-6$
. For every
$6g-6$
. For every
![]() $i \in \{1,\ldots ,3g-3\}$
, the action of the Dehn twist
$i \in \{1,\ldots ,3g-3\}$
, the action of the Dehn twist
![]() $T_{\gamma _i}$
in Fenchel–Nielsen coordinates corresponds to leaving all coordinates constant except for
$T_{\gamma _i}$
in Fenchel–Nielsen coordinates corresponds to leaving all coordinates constant except for
![]() $\tau _i$
, which gets changed by the transformation
$\tau _i$
, which gets changed by the transformation
![]() $\tau _i \mapsto \tau _i + \ell _i$
.
$\tau _i \mapsto \tau _i + \ell _i$
.
Exercise 3.4. Using Fenchel–Nielsen coordinates, the collar lemma, Dehn twists, and your geometric intuition, come up with an explanation of the following fact: a marked hyperbolic structure on Teichmüller space escapes to infinity, that is, leaves every compact set, if and only if some fixed geodesic becomes arbitrarily long.
Let us highlight an interesting feature of a geodesic pair of pants decompositions of hyperbolic surfaces. By the work of Bers [Reference BersBer85], every closed, connected, oriented hyperbolic surface admits a geodesic pair of pants decompositions whose cuffs have lengths bounded by a linear function of g. Buser conjectured this result can be improved to ensure the cuffs have lengths bounded by a linear function of
![]() $\sqrt {g}$
[Reference BuserBus92]. This conjecture remains open until today.
$\sqrt {g}$
[Reference BuserBus92]. This conjecture remains open until today.
Exercise 3.5. Show that there are finitely many pairs of pants decompositions of
![]() $S_g$
up to homeomorphism. Can you give an asymptotic estimate for the number of such equivalence classes? Hint: If
$S_g$
up to homeomorphism. Can you give an asymptotic estimate for the number of such equivalence classes? Hint: If
![]() $I_N$
denotes the number of isomorphism classes of cubic multigraphs on N vertices, then, as
$I_N$
denotes the number of isomorphism classes of cubic multigraphs on N vertices, then, as
![]() $N \to \infty $
,
$N \to \infty $
,
 $$ \begin{align*} I_N \sim \frac{e^2}{\sqrt{\pi N}} \cdot \bigg( \frac{3N}{4e}\bigg)^{N/2}. \end{align*} $$
$$ \begin{align*} I_N \sim \frac{e^2}{\sqrt{\pi N}} \cdot \bigg( \frac{3N}{4e}\bigg)^{N/2}. \end{align*} $$
Exercise 3.6. Use Bers’s theorem and Exercise 3.5 to show that for every
![]() $\epsilon> 0$
, the subset
$\epsilon> 0$
, the subset
![]() $K_\epsilon \subseteq \mathcal {M}_g$
of genus g hyperbolic surfaces, all of whose closed geodesics have length
$K_\epsilon \subseteq \mathcal {M}_g$
of genus g hyperbolic surfaces, all of whose closed geodesics have length
![]() $\geq \epsilon $
, is compact. This result is commonly known as Mumford’s compactness criterion. Hint: Using Fenchel–Nielsen coordinates, write
$\geq \epsilon $
, is compact. This result is commonly known as Mumford’s compactness criterion. Hint: Using Fenchel–Nielsen coordinates, write
![]() $K_\epsilon \subseteq \mathcal {M}_g$
as a union of finitely many projections of compact subsets of
$K_\epsilon \subseteq \mathcal {M}_g$
as a union of finitely many projections of compact subsets of
![]() $\mathcal {T}_g$
.
$\mathcal {T}_g$
.
3.8 The Weil–Petersson measure on Teichmüller space
The discussion above suggests considering the following volume form on Teichmüller space: given a set of Fenchel–Nielsen coordinates
![]() $(\ell _i,\tau _i)_{i=1}^{3g-3} \in \smash {(\mathbb {R}_+ \times \mathbb {R})^{3g-3}}$
, denote by
$(\ell _i,\tau _i)_{i=1}^{3g-3} \in \smash {(\mathbb {R}_+ \times \mathbb {R})^{3g-3}}$
, denote by
![]() $v_{\mathrm {wp}}$
the Weil–Petersson volume form on
$v_{\mathrm {wp}}$
the Weil–Petersson volume form on
![]() $\mathcal {T}_g$
given by
$\mathcal {T}_g$
given by
 $$ \begin{align} v_{\mathrm{wp}} := \bigwedge_{i=1}^{3g-3} d\ell_i \wedge d\tau_i. \end{align} $$
$$ \begin{align} v_{\mathrm{wp}} := \bigwedge_{i=1}^{3g-3} d\ell_i \wedge d\tau_i. \end{align} $$
This volume form is independent of the choice of Fenchel–Nielsen coordinates and, in particular, is mapping class group invariant. This fact is a consequence of a deep result of Wolpert known as Wolpert’s magic formula [Reference WolpertWol83]. We refer to the corresponding measure
![]() $\mu _{\mathrm {wp}}$
as the Weil–Petersson measure of
$\mu _{\mathrm {wp}}$
as the Weil–Petersson measure of
![]() $\mathcal {T}_g$
.
$\mathcal {T}_g$
.
3.9 Local pushforwards of measures
In the upcoming discussion, we make use of the following abstract measure theoretic construction. Let X be a locally compact, Hausdorff, second countable topological space endowed with a properly discontinuous action of a discrete group G. Notice that
![]() $X/G$
is also locally compact, Hausdorff, and second countable. Let
$X/G$
is also locally compact, Hausdorff, and second countable. Let
![]() $\pi \colon X \to X/G$
be the corresponding quotient map. As the action of G on X is properly discontinuous, one can cover X by open subsets
$\pi \colon X \to X/G$
be the corresponding quotient map. As the action of G on X is properly discontinuous, one can cover X by open subsets
![]() $U \subseteq X$
invariant under the action of finite subgroups
$U \subseteq X$
invariant under the action of finite subgroups
![]() $\Gamma _U < G$
and such that
$\Gamma _U < G$
and such that
![]() $gU \cap U = \emptyset $
for all
$gU \cap U = \emptyset $
for all
![]() $g \in G \setminus \Gamma _U$
. Open sets
$g \in G \setminus \Gamma _U$
. Open sets
![]() $U/\Gamma _U \subseteq X/G$
of this form will be referred to as well covered.
$U/\Gamma _U \subseteq X/G$
of this form will be referred to as well covered.
Given a locally finite G-invariant Borel measure
![]() $\mu $
on X, there exists a unique locally finite Borel measure
$\mu $
on X, there exists a unique locally finite Borel measure
![]() $\pi _\# \mu $
on
$\pi _\# \mu $
on
![]() $X/G$
satisfying the following property: if
$X/G$
satisfying the following property: if
![]() $U/\Gamma _U \subseteq X/G$
is a well-covered open set,
$U/\Gamma _U \subseteq X/G$
is a well-covered open set,
where
![]() $(\pi |_U)_* (\mu |_U)$
denotes the usual pushforward of the measure
$(\pi |_U)_* (\mu |_U)$
denotes the usual pushforward of the measure
![]() $\mu |_U$
through the map
$\mu |_U$
through the map
![]() $\pi |_U$
. We refer to the measure
$\pi |_U$
. We refer to the measure
![]() $\pi _\# \mu $
as the local pushfoward of
$\pi _\# \mu $
as the local pushfoward of
![]() $\mu $
to
$\mu $
to
![]() $X/G$
.
$X/G$
.
Exercise 3.7. Check that the definition of
![]() $\pi _\# \mu $
gives rise to a unique well-defined measure on
$\pi _\# \mu $
gives rise to a unique well-defined measure on
![]() $X/G$
.
$X/G$
.
3.10 The Weil–Petersson measure on moduli space
Recall that the quotient
![]() $\mathcal {M}_g := \mathcal {T}_g /\mathrm {Mod}_g$
is the moduli space of genus g hyperbolic surfaces. As the action of
$\mathcal {M}_g := \mathcal {T}_g /\mathrm {Mod}_g$
is the moduli space of genus g hyperbolic surfaces. As the action of
![]() $\mathrm {Mod}_g$
on
$\mathrm {Mod}_g$
on
![]() $\mathcal {T}_g$
is properly discontinuous and preserves the Weil–Petersson measure
$\mathcal {T}_g$
is properly discontinuous and preserves the Weil–Petersson measure
![]() $\mu _{\mathrm {wp}}$
, one can consider the local pushforward of
$\mu _{\mathrm {wp}}$
, one can consider the local pushforward of
![]() $\mu _{\mathrm {wp}}$
to
$\mu _{\mathrm {wp}}$
to
![]() $\mathcal {M}_g$
. We denote this measure by
$\mathcal {M}_g$
. We denote this measure by
![]() $\widehat {\mu }_{\mathrm {wp}}$
and refer to it as the Weil–Petersson measure of
$\widehat {\mu }_{\mathrm {wp}}$
and refer to it as the Weil–Petersson measure of
![]() $\mathcal {M}_g$
.
$\mathcal {M}_g$
.
Exercise 3.8. Using Bers’s theorem and Exercise 3.5, show that the Weil–Petersson measure
![]() $\widehat {\mu }_{\mathrm {wp}}$
on
$\widehat {\mu }_{\mathrm {wp}}$
on
![]() $\mathcal {M}_g$
is finite. Can you give a bound on the total Weil–Petersson measure
$\mathcal {M}_g$
is finite. Can you give a bound on the total Weil–Petersson measure
![]() $\widehat {\mu }_{\mathrm {wp}}(\mathcal {M}_g)$
? Hint: Follow a similar approach as in Exercise 3.6.
$\widehat {\mu }_{\mathrm {wp}}(\mathcal {M}_g)$
? Hint: Follow a similar approach as in Exercise 3.6.
Mirzakhani and Zograf [Reference Mirzakhani and ZografMZ15] proved asymptotic estimates for the total Weil–Petersson volumes
![]() $\widehat {\mu }_{\mathrm {wp}}(\mathcal {M}_g)$
as
$\widehat {\mu }_{\mathrm {wp}}(\mathcal {M}_g)$
as
![]() $g \to \infty $
that wildly differ from the rough upper bound one can obtain by following the hint in Exercise 3.8. The finiteness of the Weil–Petersson measure on moduli space suggests studying random hyperbolic surfaces sampled according to this measure. This has become a very active field of study in recent years. As a starting point for curious readers, we recommend [Reference Lipnowski and WrightLW24, Reference MirzakhaniMir13, Reference MonkMon22, Reference Mirzakhani and PetriMP19, Reference Monk and ThomasMT20, Reference Mirzakhani and ZografMZ15].
$g \to \infty $
that wildly differ from the rough upper bound one can obtain by following the hint in Exercise 3.8. The finiteness of the Weil–Petersson measure on moduli space suggests studying random hyperbolic surfaces sampled according to this measure. This has become a very active field of study in recent years. As a starting point for curious readers, we recommend [Reference Lipnowski and WrightLW24, Reference MirzakhaniMir13, Reference MonkMon22, Reference Mirzakhani and PetriMP19, Reference Monk and ThomasMT20, Reference Mirzakhani and ZografMZ15].
3.11 Simple closed multi-curves
We refer to a parameterized simple closed curve on
![]() $S_g$
up to homotopy and orientation reversal as a simple closed curve. We will always assume simple closed curves on
$S_g$
up to homotopy and orientation reversal as a simple closed curve. We will always assume simple closed curves on
![]() $S_g$
are homotopically non-trivial. The group
$S_g$
are homotopically non-trivial. The group
![]() $\mathrm {Mod}_g$
acts naturally on these equivalence classes. Given a marked hyperbolic structure
$\mathrm {Mod}_g$
acts naturally on these equivalence classes. Given a marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
, every simple closed curve on
$X \in \mathcal {T}_g$
, every simple closed curve on
![]() $S_g$
corresponds to a unique simple closed geodesic on X. Through this perspective, counting problems for simple closed geodesics on X can be easily reformulated as counting problems for simple closed curves on
$S_g$
corresponds to a unique simple closed geodesic on X. Through this perspective, counting problems for simple closed geodesics on X can be easily reformulated as counting problems for simple closed curves on
![]() $S_g$
.
$S_g$
.
Exercise 3.9. The
![]() $9g-9$
theorem, see for instance [Reference Farb and MargalitFM12, Theorem 10.7], guarantees that a marked hyperbolic structure
$9g-9$
theorem, see for instance [Reference Farb and MargalitFM12, Theorem 10.7], guarantees that a marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
is completely determined by its simple marked length spectrum, that is, by the function which to every simple closed curve
$X \in \mathcal {T}_g$
is completely determined by its simple marked length spectrum, that is, by the function which to every simple closed curve
![]() $\gamma $
on
$\gamma $
on
![]() $S_g$
assigns the length
$S_g$
assigns the length
![]() $\ell _{\gamma }(X)$
of its unique geodesic representative with respect to X. Using this theorem and Dehn–Thurston coordinates, show that the kernel of the action of
$\ell _{\gamma }(X)$
of its unique geodesic representative with respect to X. Using this theorem and Dehn–Thurston coordinates, show that the kernel of the action of
![]() $\mathrm {Mod}_g$
on
$\mathrm {Mod}_g$
on
![]() $\mathcal {T}_g$
is equal to the kernel of the action of
$\mathcal {T}_g$
is equal to the kernel of the action of
![]() $\mathrm {Mod}_g$
on the set of simple closed curves on
$\mathrm {Mod}_g$
on the set of simple closed curves on
![]() $S_g$
.
$S_g$
.
More generally, a simple closed multi-curve on
![]() $S_g$
is a formal sum
$S_g$
is a formal sum
![]() $\gamma = \smash {\sum _{i=1}^k} a_i \gamma _i$
of distinct simple closed curves on
$\gamma = \smash {\sum _{i=1}^k} a_i \gamma _i$
of distinct simple closed curves on
![]() $S_g$
that can be realized disjointly, together with real positive weights
$S_g$
that can be realized disjointly, together with real positive weights
![]() $a_i \in \mathbb {R}_+$
. Given
$a_i \in \mathbb {R}_+$
. Given
![]() $X \in \mathcal {T}_g$
, we define
$X \in \mathcal {T}_g$
, we define
![]() $\ell _{\gamma }(X) := \smash {\sum _{i=1}^k a_i \ell _{\gamma _i}(X)}$
. An integral simple closed multi-curve on
$\ell _{\gamma }(X) := \smash {\sum _{i=1}^k a_i \ell _{\gamma _i}(X)}$
. An integral simple closed multi-curve on
![]() $S_g$
is a simple closed multi-curve all of whose weights are integral. The group
$S_g$
is a simple closed multi-curve all of whose weights are integral. The group
![]() $\mathrm {Mod}_g$
acts naturally on simple closed multi-curves by acting on each of the components of the formal sum. We think of
$\mathrm {Mod}_g$
acts naturally on simple closed multi-curves by acting on each of the components of the formal sum. We think of
![]() $\mathrm {Mod}_g$
acting on integral simple closed multi-curves as an analog of
$\mathrm {Mod}_g$
acting on integral simple closed multi-curves as an analog of
![]() $\mathrm {SL}(2,\mathbb {Z})$
acting on
$\mathrm {SL}(2,\mathbb {Z})$
acting on
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
We say two simple closed multi-curves on
![]() $S_g$
have the same topological type if they belong to the same mapping class group orbit. More generally, we say two simple closed multi-curves on homeomorphic surfaces have the same topological type if there exists a homeomorphism between the surfaces mapping one simple closed multi-curve to the other. See Figure 10 for examples of simple closed curves of different topological types. We think of integral simple closed multi-curves on
$S_g$
have the same topological type if they belong to the same mapping class group orbit. More generally, we say two simple closed multi-curves on homeomorphic surfaces have the same topological type if there exists a homeomorphism between the surfaces mapping one simple closed multi-curve to the other. See Figure 10 for examples of simple closed curves of different topological types. We think of integral simple closed multi-curves on
![]() $S_g$
of a fixed topological type as an analog of
$S_g$
of a fixed topological type as an analog of
![]() $\mathbb {Z}^2_{\mathrm {prim}}$
.
$\mathbb {Z}^2_{\mathrm {prim}}$
.

Figure 10 Simple closed curves of different topological types on a genus
![]() $2$
surface (colour online).
$2$
surface (colour online).
3.12 Measured geodesic laminations
Just as the integer lattice
![]() $\mathbb {Z}^2$
sits inside the continuum
$\mathbb {Z}^2$
sits inside the continuum
![]() $\mathbb {R}^2$
, we would like to have a continuum interpolating between integral simple closed multi-curves on
$\mathbb {R}^2$
, we would like to have a continuum interpolating between integral simple closed multi-curves on
![]() $S_g$
. Although we will not need it explicitly, let us give a geometric description of how objects in this continuum look like. Fix a marked hyperbolic structure
$S_g$
. Although we will not need it explicitly, let us give a geometric description of how objects in this continuum look like. Fix a marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
. A geodesic lamination on X is a closed subset of X that can be written as a disjoint union of simple geodesics. The most basic example of a geodesic lamination is a union of disjoint simple closed geodesics. See Figure 11 for a more complicated example. Very commonly, the intersection of a geodesic lamination with a transverse arc is a fractal set, making it hard to draw non-trivial examples.
$X \in \mathcal {T}_g$
. A geodesic lamination on X is a closed subset of X that can be written as a disjoint union of simple geodesics. The most basic example of a geodesic lamination is a union of disjoint simple closed geodesics. See Figure 11 for a more complicated example. Very commonly, the intersection of a geodesic lamination with a transverse arc is a fractal set, making it hard to draw non-trivial examples.

Figure 11 A non-trivial example of a geodesic lamination on a genus
![]() $2$
surface (colour online).
$2$
surface (colour online).
A measured geodesic lamination is a geodesic lamination endowed with a fully supported invariant transverse measure. The transverse measure assigns a finite Borel measure to every arc transverse to the lamination. This assignment is invariant under splitting of arcs and homotopies preserving the leaves of the lamination. Not every lamination admits a fully supported invariant transverse measure.
Exercise 3.10. Show that the geodesic lamination in Figure 11 does not admit a fully supported invariant transverse measure. Hint: Consider an arc going across the middle closed geodesic.
The different spaces of measured geodesic laminations obtained as X varies over
![]() $\mathcal {T}_g$
can be canonically identified to each other. We will denote by
$\mathcal {T}_g$
can be canonically identified to each other. We will denote by
![]() $\mathcal {ML}_g$
any such space and refer to it as the space of measured geodesic laminations on
$\mathcal {ML}_g$
any such space and refer to it as the space of measured geodesic laminations on
![]() $S_g$
. Simple closed multi-curves embed naturally into
$S_g$
. Simple closed multi-curves embed naturally into
![]() $\mathcal {ML}_g$
by considering their geodesic representatives and endowing them with appropriately weighted transverse Dirac measures. We denote by
$\mathcal {ML}_g$
by considering their geodesic representatives and endowing them with appropriately weighted transverse Dirac measures. We denote by
![]() $\mathcal {ML}_g(\mathbb {Z}) \subseteq \mathcal {ML}_g$
the set of integral simple closed multi-curves on
$\mathcal {ML}_g(\mathbb {Z}) \subseteq \mathcal {ML}_g$
the set of integral simple closed multi-curves on
![]() $S_g$
.
$S_g$
.
The space
![]() $\mathcal {ML}_g$
can be topologized in such a way that rationally weighted simple closed multi-curves on
$\mathcal {ML}_g$
can be topologized in such a way that rationally weighted simple closed multi-curves on
![]() $S_g$
are dense in it. The action of
$S_g$
are dense in it. The action of
![]() $\mathrm {Mod}_g$
on simple closed multi-curves extends continuously to an action on
$\mathrm {Mod}_g$
on simple closed multi-curves extends continuously to an action on
![]() $\mathcal {ML}_g$
. We think of
$\mathcal {ML}_g$
. We think of
![]() $\mathrm {Mod}_g$
acting on
$\mathrm {Mod}_g$
acting on
![]() $\mathcal {ML}_g$
as an analog of
$\mathcal {ML}_g$
as an analog of
![]() $\mathrm {SL}(2,\mathbb {Z})$
acting on
$\mathrm {SL}(2,\mathbb {Z})$
acting on
![]() $\mathbb {R}^2$
. By the work of Thurston [Reference ThurstonThu80], the length
$\mathbb {R}^2$
. By the work of Thurston [Reference ThurstonThu80], the length
![]() $\ell _\unicode{x3bb} (X)> 0$
of a measured geodesic lamination
$\ell _\unicode{x3bb} (X)> 0$
of a measured geodesic lamination
![]() $\unicode{x3bb} \in \mathcal {ML}_g$
with respect to a marked hyperbolic structure
$\unicode{x3bb} \in \mathcal {ML}_g$
with respect to a marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
can be defined in a unique continuous way extending the definition on simple closed multi-curves introduced above.
$X \in \mathcal {T}_g$
can be defined in a unique continuous way extending the definition on simple closed multi-curves introduced above.
3.13 Dehn–Thurston coordinates
In a similar spirit to how hyperbolic surfaces can be constructed by gluing hyperbolic pairs of pants with geodesic boundary components, integral simple closed multi-curves on surfaces can be constructed by gluing simple arc systems on pairs of pants. By an arc on a pair of pants, we will always mean an arc joining two of its boundary components. Every simple arc on a pair of pants is isotopic to exactly one of the six arcs represented in Figure 12; here, we allow the isotopy to move points on the boundary of the pair of pants. Every simple arc system on a pair of pants is isotopic to an arc system constructed by taking disjoint parallel copies of these arcs. Given an assignment of non-negative integers
![]() $(a,b,c) \in \mathbb{N}$
to the boundary components of a pair of pants satisfying
$(a,b,c) \in \mathbb{N}$
to the boundary components of a pair of pants satisfying
![]() $a+b+c \in 2\mathbb{N}$
, there exists a unique, up to isotopy, arc system realizing
$a+b+c \in 2\mathbb{N}$
, there exists a unique, up to isotopy, arc system realizing
![]() $(a,b,c)$
as the number of intersections of the arc system with the boundary components.
$(a,b,c)$
as the number of intersections of the arc system with the boundary components.

Figure 12 The six isotopy classes of simple arcs in a pair of pants (colour online).
Given simple arc systems on pairs of pants glued along two of their boundary components, these arc systems can be glued together if and only if the number of times they intersect the glued boundary components is the same. There exist
![]() $\mathbb {Z}$
many different ways of gluing these arc systems depending on how much we twist one with respect to the other before gluing them together.
$\mathbb {Z}$
many different ways of gluing these arc systems depending on how much we twist one with respect to the other before gluing them together.
Let
![]() $\mathcal {P}:=(\gamma _i)_{i=1}^{3g-3}$
be a pair of pants decomposition of
$\mathcal {P}:=(\gamma _i)_{i=1}^{3g-3}$
be a pair of pants decomposition of
![]() $S_g$
. Following the discussion above, we can parameterize integral simple closed multi-curves on
$S_g$
. Following the discussion above, we can parameterize integral simple closed multi-curves on
![]() $S_g$
in terms of intersection numbers
$S_g$
in terms of intersection numbers
![]() $m_i \in \mathbb{N}$
and twisting numbers
$m_i \in \mathbb{N}$
and twisting numbers
![]() $t_i \in \mathbb {Z}$
with respect to the components of
$t_i \in \mathbb {Z}$
with respect to the components of
![]() $\mathcal {P}$
. Consider the parameter space
$\mathcal {P}$
. Consider the parameter space
 $$ \begin{align*} \Sigma:= \prod_{i=1}^{3g-3} (\mathbb {R}_{\geq 0} \times \mathbb {R})/\sim, \end{align*} $$
$$ \begin{align*} \Sigma:= \prod_{i=1}^{3g-3} (\mathbb {R}_{\geq 0} \times \mathbb {R})/\sim, \end{align*} $$
where
![]() $\sim $
denotes the equivalence relation on
$\sim $
denotes the equivalence relation on
![]() $\mathbb {R}_{\geq 0} \times \mathbb {R}$
identifying
$\mathbb {R}_{\geq 0} \times \mathbb {R}$
identifying
![]() $(0,t) \sim (0,-t)$
for every
$(0,t) \sim (0,-t)$
for every
![]() $t \in \mathbb {R}$
. The parameters
$t \in \mathbb {R}$
. The parameters
![]() $\smash {(m_i,t_i)_{i=1}^{3g-3}}$
give rise to a bijection between the set of integral simple closed multi-curves on
$\smash {(m_i,t_i)_{i=1}^{3g-3}}$
give rise to a bijection between the set of integral simple closed multi-curves on
![]() $S_g$
and the set of integral points in
$S_g$
and the set of integral points in
![]() $\Sigma $
such that for every complementary region R of
$\Sigma $
such that for every complementary region R of
![]() $S_{g,n} \backslash \mathcal {P}$
, the parameters
$S_{g,n} \backslash \mathcal {P}$
, the parameters
![]() $m_i$
corresponding to components
$m_i$
corresponding to components
![]() $\gamma _i$
of
$\gamma _i$
of
![]() $\mathcal {P}$
bounding R add up to an even number; this parity restriction comes from the fact that every strand of a multi-curve that enters a pair of pants must also exit it. If
$\mathcal {P}$
bounding R add up to an even number; this parity restriction comes from the fact that every strand of a multi-curve that enters a pair of pants must also exit it. If
![]() $m_i = 0$
and
$m_i = 0$
and
![]() $t_i = t \in \mathbb {Z}$
, the corresponding simple closed multi-curve has
$t_i = t \in \mathbb {Z}$
, the corresponding simple closed multi-curve has
![]() $|t|$
disjoint parallel copies of
$|t|$
disjoint parallel copies of
![]() $\gamma _i$
. We refer to the parameters
$\gamma _i$
. We refer to the parameters
![]() $\smash {(m_i,t_i)_{i=1}^{3g-3}}$
as a set of Dehn–Thurston coordinates.
$\smash {(m_i,t_i)_{i=1}^{3g-3}}$
as a set of Dehn–Thurston coordinates.
Although we have not defined twisting numbers precisely, we can easily describe the effect of changing them by a given amount. See Figure 13 for an example. In particular, for every
![]() $i \in \{1,\ldots ,3g-3\}$
, the action of the Dehn twist
$i \in \{1,\ldots ,3g-3\}$
, the action of the Dehn twist
![]() $T_{\gamma _i}$
in Dehn–Thurston coordinates corresponds to leaving all coordinates constant except for
$T_{\gamma _i}$
in Dehn–Thurston coordinates corresponds to leaving all coordinates constant except for
![]() $t_i$
which gets changed by the transformation
$t_i$
which gets changed by the transformation
![]() $t_i \mapsto t_i + m_i$
.
$t_i \mapsto t_i + m_i$
.

Figure 13 The effect of changing a twist coordinate by
![]() $t_i \mapsto t_i+1$
(colour online).
$t_i \mapsto t_i+1$
(colour online).
By the work of Thurston [Reference ThurstonThu80], the parameterization of
![]() $\mathcal {ML}_g(\mathbb {Z})$
provided by any set of Dehn–Thurston coordinates extends to a homeomorphism between
$\mathcal {ML}_g(\mathbb {Z})$
provided by any set of Dehn–Thurston coordinates extends to a homeomorphism between
![]() $\mathcal {ML}_g$
and the parameter space
$\mathcal {ML}_g$
and the parameter space
![]() $\Sigma $
. This shows in particular that
$\Sigma $
. This shows in particular that
![]() $\mathcal {ML}_g$
is homeomorphic to
$\mathcal {ML}_g$
is homeomorphic to
![]() $\mathbb {R}^{6g-6}$
. For more details on the definition and properties of Dehn–Thurston coordinates, we refer the reader to [Reference Penner and HarerPH92, §1.2].
$\mathbb {R}^{6g-6}$
. For more details on the definition and properties of Dehn–Thurston coordinates, we refer the reader to [Reference Penner and HarerPH92, §1.2].
3.14 The Thurston measure
The Thurston measure
![]() $\mu _{\mathrm {Thu}}$
on
$\mu _{\mathrm {Thu}}$
on
![]() $\mathcal {ML}_g$
is the pullback of the Lebesgue measure on the parameter space
$\mathcal {ML}_g$
is the pullback of the Lebesgue measure on the parameter space
![]() $\Sigma $
of any set of Dehn–Thurston coordinates. This measure is well defined, that is, independent of the choice of Dehn–Thurston coordinates. Indeed, in analogy with the case of the Lebesgue measure, one can characterize
$\Sigma $
of any set of Dehn–Thurston coordinates. This measure is well defined, that is, independent of the choice of Dehn–Thurston coordinates. Indeed, in analogy with the case of the Lebesgue measure, one can characterize
![]() $\mu _{\mathrm {Thu}}$
as the weak-
$\mu _{\mathrm {Thu}}$
as the weak-
![]() $\star $
limit of a family of rescaled integral simple closed multi-curve counting measures. Consider the natural
$\star $
limit of a family of rescaled integral simple closed multi-curve counting measures. Consider the natural
![]() $\mathbb {R}_+$
action on
$\mathbb {R}_+$
action on
![]() $\mathcal {ML}_g$
scaling transverse measures. This action corresponds to the natural scaling action of
$\mathcal {ML}_g$
scaling transverse measures. This action corresponds to the natural scaling action of
![]() $\mathbb {R}_+$
on
$\mathbb {R}_+$
on
![]() $\Sigma $
via the identification by Dehn–Thurston coordinates. For every
$\Sigma $
via the identification by Dehn–Thurston coordinates. For every
![]() $L> 0$
, consider the rescaled counting measure
$L> 0$
, consider the rescaled counting measure
 $$ \begin{align*} \mu_L := \frac{1}{L^{6g-6}} \sum_{\gamma \in \mathcal{ML}_g(\mathbb {Z})} \delta_{{1}/{L} \cdot \gamma}. \end{align*} $$
$$ \begin{align*} \mu_L := \frac{1}{L^{6g-6}} \sum_{\gamma \in \mathcal{ML}_g(\mathbb {Z})} \delta_{{1}/{L} \cdot \gamma}. \end{align*} $$
Exercise 3.11. Show that the sequence of rescaled counting measures
![]() $(\mu _L)_{L> 0}$
on
$(\mu _L)_{L> 0}$
on
![]() $\mathcal {ML}_g$
converges in the weak-
$\mathcal {ML}_g$
converges in the weak-
![]() $\star $
topology as
$\star $
topology as
![]() $L \to \infty $
to the pullback of the Lebesgue measure on
$L \to \infty $
to the pullback of the Lebesgue measure on
![]() $\Sigma $
under the identification with
$\Sigma $
under the identification with
![]() $\mathcal {ML}_g$
induced by any set Dehn–Thurston coordinates.
$\mathcal {ML}_g$
induced by any set Dehn–Thurston coordinates.
Directly from Exercise 3.11, we deduce
![]() $\mu _{\mathrm {Thu}}$
is invariant with respect to the
$\mu _{\mathrm {Thu}}$
is invariant with respect to the
![]() $\mathrm {Mod}_g$
action on
$\mathrm {Mod}_g$
action on
![]() $\mathcal {ML}_g$
. The definition of
$\mathcal {ML}_g$
. The definition of
![]() $\mu _{\mathrm {Thu}}$
in terms of Dehn–Thurston coordinates guarantees it satisfies the following scaling property: for every Borel measurable subset
$\mu _{\mathrm {Thu}}$
in terms of Dehn–Thurston coordinates guarantees it satisfies the following scaling property: for every Borel measurable subset
![]() $A \subseteq \mathcal {ML}_{g}$
and every
$A \subseteq \mathcal {ML}_{g}$
and every
![]() $t> 0$
,
$t> 0$
,
This follows from Exercise 3.11 and the same property for the Lebesgue measure.
Exercise 3.12. Let
![]() $f \colon \mathcal {ML}_g \to \mathbb {R}$
be a non-negative, continuous function. Suppose that f is homogeneous with respect to the
$f \colon \mathcal {ML}_g \to \mathbb {R}$
be a non-negative, continuous function. Suppose that f is homogeneous with respect to the
![]() $\mathbb {R}_+$
scaling action on
$\mathbb {R}_+$
scaling action on
![]() $\mathcal {ML}_g$
. Using equation (3.3), show that, for every
$\mathcal {ML}_g$
. Using equation (3.3), show that, for every
![]() $c> 0$
,
$c> 0$
,
3.15 Analogies with the lattice setting
Let us finish this section by highlighting some analogies that will be useful to have in mind when proving Theorem 1.1. The proof of Theorem 1.1 will follow the same approach as the proof of Theorem 2.1, but will use the analogies in Table 1 together with important results of Mirzakhani that will be discussed in §4.
Table 1 Analogies between the lattice and surface settings.

4 Weil–Petersson volumes and Mirzakhani’s integration formulas
4.1 Outline of this section
In this section, we discuss two remarkable results of Mirzhakhani that will play a crucial role in the proof of Theorem 1.1. The first of these results corresponds to the fact that the total Weil–Petersson volume of any moduli space of hyperbolic surfaces with totally geodesic boundary components is a polynomial on the lengths of the boundary components; see Theorem 4.1. The second of these results corresponds to Mirzakahani’s integration formulas over moduli space; see Exercise 4.7. We focus most of our attention on the second of these results. For the first result, we sketch a proof in the case of tori with one boundary component. An important part of the intuition behind this section comes from analogous facts for the Haar measure; see Proposition 2.10.
4.2 Surfaces with boundary
The first result we discuss concerns moduli spaces of hyperbolic surfaces with totally geodesic boundary components and their total Weil–Petersson volumes. To state this result precisely, we first introduce some notation. As many of the definitions that follow are analogous to those discussed in the previous section, we do not spend much time covering them.
Let
![]() $g,b \geq 0$
be a pair of non-negative integers such that
$g,b \geq 0$
be a pair of non-negative integers such that
![]() $2 - 2g - b < 0$
. Fix a connected, oriented, compact surface
$2 - 2g - b < 0$
. Fix a connected, oriented, compact surface
![]() $\smash {S_{g,b}}$
of genus g with b labeled boundary components
$\smash {S_{g,b}}$
of genus g with b labeled boundary components
![]() $\beta _1,\ldots ,\beta _{b}$
. Denote by
$\beta _1,\ldots ,\beta _{b}$
. Denote by
![]() $\smash {\text {Mod}_{g,b}}$
the mapping class group of
$\smash {\text {Mod}_{g,b}}$
the mapping class group of
![]() $\smash {S_{g,b}}$
, that is, the group of orientation-preserving homeomorphisms of
$\smash {S_{g,b}}$
, that is, the group of orientation-preserving homeomorphisms of
![]() $\smash {S_{g,b}}$
that setwise fix each boundary component, up to homotopy, setwise fixing each boundary component. We warn the reader that different conventions are adopted elsewhere in the literature with regard to mapping classes fixing boundary components either pointwise or setwise; this is not an issue as long as the corresponding definitions are appropriately adapted.
$\smash {S_{g,b}}$
that setwise fix each boundary component, up to homotopy, setwise fixing each boundary component. We warn the reader that different conventions are adopted elsewhere in the literature with regard to mapping classes fixing boundary components either pointwise or setwise; this is not an issue as long as the corresponding definitions are appropriately adapted.
Let
![]() $\smash {\mathbf {L}:= (L_i)_{i=1}^{b}} \in \smash {(\mathbb {R}_{>0})^{b}}$
be a vector of positive real numbers. Denote by
$\smash {\mathbf {L}:= (L_i)_{i=1}^{b}} \in \smash {(\mathbb {R}_{>0})^{b}}$
be a vector of positive real numbers. Denote by
![]() $\mathcal {T}_{g,b}(\mathbf {L})$
the Teichmüller space of marked, oriented hyperbolic structures on
$\mathcal {T}_{g,b}(\mathbf {L})$
the Teichmüller space of marked, oriented hyperbolic structures on
![]() $S_{g,b}$
with labeled geodesic boundary components whose lengths are given by
$S_{g,b}$
with labeled geodesic boundary components whose lengths are given by
![]() $\mathbf {L}$
, up to isotopy fixing each boundary component setwise. The mapping class group
$\mathbf {L}$
, up to isotopy fixing each boundary component setwise. The mapping class group
![]() $\smash {\text {Mod}_{g,b}}$
acts properly discontinuously on
$\smash {\text {Mod}_{g,b}}$
acts properly discontinuously on
![]() $\mathcal {T}_{g,b}(\mathbf {L})$
by changing the markings. The quotient
$\mathcal {T}_{g,b}(\mathbf {L})$
by changing the markings. The quotient
![]() $\mathcal {M}_{g,b}(\mathbf {L}) := \mathcal {T}_{g,b}(\mathbf {L}) / \text {Mod}_{g,b}$
is the moduli space of oriented hyperbolic structures on
$\mathcal {M}_{g,b}(\mathbf {L}) := \mathcal {T}_{g,b}(\mathbf {L}) / \text {Mod}_{g,b}$
is the moduli space of oriented hyperbolic structures on
![]() $S_{g,b}$
with labeled geodesic boundary components whose lengths are given by
$S_{g,b}$
with labeled geodesic boundary components whose lengths are given by
![]() $\mathbf {L}$
.
$\mathbf {L}$
.
4.3 Weil–Petersson volumes
The Teichmüller space
![]() $\mathcal {T}_{g,b}(\mathbf {L})$
can be parameterized using Fenchel–Nielsen coordinates in a similar way as for closed surfaces. More concretely, for any pair of pants decomposition
$\mathcal {T}_{g,b}(\mathbf {L})$
can be parameterized using Fenchel–Nielsen coordinates in a similar way as for closed surfaces. More concretely, for any pair of pants decomposition
![]() $\mathcal {P}:= \smash {(\gamma _i)_{i=1}^{3g-3+b}}$
of
$\mathcal {P}:= \smash {(\gamma _i)_{i=1}^{3g-3+b}}$
of
![]() $S_{g,b}$
, the length and twist parameters
$S_{g,b}$
, the length and twist parameters
![]() $(\ell _i,\tau _i)_{i=1}^{3g-3+b}$
of marked hyperbolic structures
$(\ell _i,\tau _i)_{i=1}^{3g-3+b}$
of marked hyperbolic structures
![]() $X \in \mathcal {T}_{g,b}(\mathbf {L})$
with respect to the components of
$X \in \mathcal {T}_{g,b}(\mathbf {L})$
with respect to the components of
![]() $\mathcal {P}$
provide a global coordinate system for
$\mathcal {P}$
provide a global coordinate system for
![]() $\mathcal {T}_{g,b}(\mathbf {L})$
; pairs of pants decompositions of surfaces with boundary are not considered to include the boundary components of the surface. The Weil–Petersson volume form
$\mathcal {T}_{g,b}(\mathbf {L})$
; pairs of pants decompositions of surfaces with boundary are not considered to include the boundary components of the surface. The Weil–Petersson volume form
![]() $v_{\mathrm {wp}}$
of
$v_{\mathrm {wp}}$
of
![]() $\mathcal {T}_{g,b}(\mathbf {L})$
can be defined as follows:
$\mathcal {T}_{g,b}(\mathbf {L})$
can be defined as follows:
 $$ \begin{align} v_{\mathrm{wp}} := \bigwedge_{i=1}^{3g-3+b} d\ell_i \wedge d\tau_i. \end{align} $$
$$ \begin{align} v_{\mathrm{wp}} := \bigwedge_{i=1}^{3g-3+b} d\ell_i \wedge d\tau_i. \end{align} $$
We refer to the measure
![]() $\mu _{\mathrm {wp}}$
induced by
$\mu _{\mathrm {wp}}$
induced by
![]() $v_{\mathrm {wp}}$
as the Weil–Petersson measure of
$v_{\mathrm {wp}}$
as the Weil–Petersson measure of
![]() $\mathcal {T}_{g,b}(\mathbf {L})$
.
$\mathcal {T}_{g,b}(\mathbf {L})$
.
On the moduli space
![]() $\mathcal {M}_{g,b}(\mathbf {L}) := \mathcal {T}_{g,b}(\mathbf {L}) / \text {Mod}_{g,b}$
, consider the local pushforward
$\mathcal {M}_{g,b}(\mathbf {L}) := \mathcal {T}_{g,b}(\mathbf {L}) / \text {Mod}_{g,b}$
, consider the local pushforward
![]() $\widehat {\mu }_{\mathrm {wp}}$
of the Weil–Petersson measure
$\widehat {\mu }_{\mathrm {wp}}$
of the Weil–Petersson measure
![]() $\mu _{\mathrm {wp}}$
. We refer to this measure as the Weil–Petersson measure of
$\mu _{\mathrm {wp}}$
. We refer to this measure as the Weil–Petersson measure of
![]() $\mathcal {M}_{g,b}(\mathbf {L})$
. The same arguments suggested in Exercise 3.8 can be used to show that the Weil–Petersson measure
$\mathcal {M}_{g,b}(\mathbf {L})$
. The same arguments suggested in Exercise 3.8 can be used to show that the Weil–Petersson measure
![]() $\widehat {\mu }_{\mathrm {wp}}$
on
$\widehat {\mu }_{\mathrm {wp}}$
on
![]() $\mathcal {M}_{g,b}(\mathbf {L})$
is finite. The total Weil–Petersson volume of
$\mathcal {M}_{g,b}(\mathbf {L})$
is finite. The total Weil–Petersson volume of
![]() $\mathcal {M}_{g,b}(\mathbf {L})$
will be denoted by
$\mathcal {M}_{g,b}(\mathbf {L})$
will be denoted by
By Exercise 3.3, if the surface
![]() $S_{g,b}$
is a pair of pants, that is, if
$S_{g,b}$
is a pair of pants, that is, if
![]() $g = 0$
and
$g = 0$
and
![]() $b = 3$
, the moduli space
$b = 3$
, the moduli space
![]() $\mathcal {M}_{g,n}^{b}(\mathbf {L})$
consists of exactly one point. In this case, we adopt the convention
$\mathcal {M}_{g,n}^{b}(\mathbf {L})$
consists of exactly one point. In this case, we adopt the convention
The following remarkable theorem of Mirzakhani shows that the total Weil–Petersson volumes
![]() $V_{g,b}(\mathbf {L}) $
are polynomials on the
$V_{g,b}(\mathbf {L}) $
are polynomials on the
![]() $\mathbf {L}$
variables. We will later sketch a proof of this result for the case of tori with one boundary component, that is, for the case
$\mathbf {L}$
variables. We will later sketch a proof of this result for the case of tori with one boundary component, that is, for the case
![]() $g=1$
and
$g=1$
and
![]() $b=1$
.
$b=1$
.
Theorem 4.1. [Reference MirzakhaniMir07a, Theorem 1.1] [Reference MirzakhaniMir07b, Theorem 1.1]
Let
![]() $g, b \geq 0$
be non-negative integers such that
$g, b \geq 0$
be non-negative integers such that
![]() $2 - 2g - b < 0$
. The total Weil–Petersson volume
$2 - 2g - b < 0$
. The total Weil–Petersson volume
is a polynomial of degree
![]() $3g-3+b$
on the variables
$3g-3+b$
on the variables
![]() $L_1^2,\ldots ,L_{b}^2$
. Moreover, if
$L_1^2,\ldots ,L_{b}^2$
. Moreover, if
 $$ \begin{align*} V_{g,b}(L_1,\ldots,L_{b}) = \sum_{\substack{\alpha \in (\mathbb {Z}_{\geq 0})^{b}\\ |\alpha| \leq 3g-3+b} } c_\alpha \cdot L_1^{2\alpha_1} \cdots L_{b}^{2\alpha_{b}}, \end{align*} $$
$$ \begin{align*} V_{g,b}(L_1,\ldots,L_{b}) = \sum_{\substack{\alpha \in (\mathbb {Z}_{\geq 0})^{b}\\ |\alpha| \leq 3g-3+b} } c_\alpha \cdot L_1^{2\alpha_1} \cdots L_{b}^{2\alpha_{b}}, \end{align*} $$
where
![]() $|\alpha | := \alpha _1 + \cdots + \alpha _{b}$
for every
$|\alpha | := \alpha _1 + \cdots + \alpha _{b}$
for every
![]() $\alpha \in (\mathbb {Z}_{\geq 0})^{b}$
, then
$\alpha \in (\mathbb {Z}_{\geq 0})^{b}$
, then
![]() $c_\alpha \in \mathbf {Q}_{>0} \cdot \pi ^{6g-6 +2b - 2|\alpha |}$
. In particular, the leading coefficients of
$c_\alpha \in \mathbf {Q}_{>0} \cdot \pi ^{6g-6 +2b - 2|\alpha |}$
. In particular, the leading coefficients of
![]() $V_{g,b}(L_1,\ldots ,L_{b})$
belong to
$V_{g,b}(L_1,\ldots ,L_{b})$
belong to
![]() $\mathbf {Q}_{> 0}$
.
$\mathbf {Q}_{> 0}$
.
4.4 The local change of variables formula
We now introduce a local change of variables formula that will be used in forthcoming discussions. Let X be a locally compact, Hausdorff, second countable topological space endowed with a properly discontinuous action of a discrete group G and
![]() $f \colon X \to \mathbb {R}$
be a measurable, non-negative function. Suppose that f is invariant with respect to a subgroup
$f \colon X \to \mathbb {R}$
be a measurable, non-negative function. Suppose that f is invariant with respect to a subgroup
![]() $H < G$
, that is,
$H < G$
, that is,
![]() $f(h.x) = f(x)$
for every
$f(h.x) = f(x)$
for every
![]() $x \in X$
and every
$x \in X$
and every
![]() $h \in H$
. Denote by
$h \in H$
. Denote by
![]() $\smash {\widetilde {f}} \colon X/H \to \mathbb {R}$
the measurable, non-negative function induced by f on
$\smash {\widetilde {f}} \colon X/H \to \mathbb {R}$
the measurable, non-negative function induced by f on
![]() $X/H$
. Consider the measurable non-negative function
$X/H$
. Consider the measurable non-negative function
![]() $\smash {\widehat {f}} \colon X/G \to \mathbb {R}$
which to every
$\smash {\widehat {f}} \colon X/G \to \mathbb {R}$
which to every
![]() $x \in X/G$
assigns the value
$x \in X/G$
assigns the value
 $$ \begin{align*} \widehat{f}(x) := \sum_{g \in G/H} f(g.x). \end{align*} $$
$$ \begin{align*} \widehat{f}(x) := \sum_{g \in G/H} f(g.x). \end{align*} $$
Let
![]() $\mu $
be a locally finite G-invariant Borel measure on X. Denote by
$\mu $
be a locally finite G-invariant Borel measure on X. Denote by
![]() $\smash {\widetilde {\mu }}$
the local pushforward of
$\smash {\widetilde {\mu }}$
the local pushforward of
![]() $\mu $
to
$\mu $
to
![]() $X/H$
and by
$X/H$
and by
![]() $\smash {\widehat {\mu }}$
the local pushforward of
$\smash {\widehat {\mu }}$
the local pushforward of
![]() $\mu $
to
$\mu $
to
![]() $X/G$
. The following exercise can be interpreted as a local change of variables formula.
$X/G$
. The following exercise can be interpreted as a local change of variables formula.
Exercise 4.2. Show that, in the setting described above, the following integration formula holds:
 $$ \begin{align*} \int_{X/G} \widehat{f}(x) \thinspace d\widehat{\mu}(x) = \int_{X/H} \widetilde{f}(y) \thinspace d\widetilde{\mu}(y). \end{align*} $$
$$ \begin{align*} \int_{X/G} \widehat{f}(x) \thinspace d\widehat{\mu}(x) = \int_{X/H} \widetilde{f}(y) \thinspace d\widetilde{\mu}(y). \end{align*} $$
Hint: Use a partition of unity of
![]() $X/G$
to reduce to the case where f is supported on the preimage of a well-covered neighborhood.
$X/G$
to reduce to the case where f is supported on the preimage of a well-covered neighborhood.
The following exercise, which corresponds to Proposition 2.10, is a classical application of the local change of variables formula in the setting of lattices.
Exercise 4.3. The main goal of this exercise is to prove Proposition 2.10; we refer the reader back to §2 for the definitions and notation that will be used throughout. Let
![]() $X := \mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
and
$X := \mathrm {SO}(2)\backslash \mathrm {SL}(2,\mathbb {R})$
and
![]() $G := \mathrm {SL}(2,\mathbb {Z})$
acting on X via right multiplication. Denote by
$G := \mathrm {SL}(2,\mathbb {Z})$
acting on X via right multiplication. Denote by
![]() $\| \cdot \|$
the Euclidean norm on
$\| \cdot \|$
the Euclidean norm on
![]() $\mathbb {R}^2$
and by
$\mathbb {R}^2$
and by
![]() $e_1 := (1,0) \in \mathbb {R}^2$
the first canonical vector of
$e_1 := (1,0) \in \mathbb {R}^2$
the first canonical vector of
![]() $\mathbb {R}^2$
. For every
$\mathbb {R}^2$
. For every
![]() $L> 0$
, consider the function
$L> 0$
, consider the function
![]() $f \colon X \to \mathbb {R}$
which to every
$f \colon X \to \mathbb {R}$
which to every
![]() $A \in X$
assigns the value
$A \in X$
assigns the value
![]() $f(A) := \mathbb {1}_{\| A \cdot e_1\| \leq L}$
. Notice that f is invariant with respect to the subgroup
$f(A) := \mathbb {1}_{\| A \cdot e_1\| \leq L}$
. Notice that f is invariant with respect to the subgroup
![]() $H < G$
generated by the unipotent matrix
$H < G$
generated by the unipotent matrix
 $$ \begin{align*} u_1 := \left(\begin{array}{@{}c c@{}} 1 & 1 \\ 0 & 1 \end{array}\right)\hspace{-1.5pt}. \end{align*} $$
$$ \begin{align*} u_1 := \left(\begin{array}{@{}c c@{}} 1 & 1 \\ 0 & 1 \end{array}\right)\hspace{-1.5pt}. \end{align*} $$
-
(1) Show that for every
 $\Lambda \in \mathcal {M}_1 := X/G$
and every
$\Lambda \in \mathcal {M}_1 := X/G$
and every
 $L> 0$
,
$L> 0$
,  $$ \begin{align*} \smash{\widehat{f}}(\Lambda) = p(\Lambda, L). \end{align*} $$
$$ \begin{align*} \smash{\widehat{f}}(\Lambda) = p(\Lambda, L). \end{align*} $$
-
(2) Show that if
 $A \in X$
gets identified with
$A \in X$
gets identified with
 $z \in \mathbf {H}^2$
, then and, in particular, for every
$z \in \mathbf {H}^2$
, then and, in particular, for every $$ \begin{align*} \|A \cdot e_1\| = \Im(z)^{-1/2}, \end{align*} $$
$$ \begin{align*} \|A \cdot e_1\| = \Im(z)^{-1/2}, \end{align*} $$
 $L> 0$
,
$L> 0$
,  $$ \begin{align*} f(A) = \mathbf{1}_{\Im(z) \geq 1/L^2}. \end{align*} $$
$$ \begin{align*} f(A) = \mathbf{1}_{\Im(z) \geq 1/L^2}. \end{align*} $$
-
(3) Denote by
 $\widehat {\mu }$
the local pushforward of the measure
$\widehat {\mu }$
the local pushforward of the measure
 $\mu $
in equation (2.13) to
$\mu $
in equation (2.13) to
 $\mathcal {M}_1$
as defined in equation (3.2). Notice this definition differs from that used in Proposition 2.10 by a factor of
$\mathcal {M}_1$
as defined in equation (3.2). Notice this definition differs from that used in Proposition 2.10 by a factor of
 $2$
. Using Exercise 4.2, the fundamental domain in Figure 2 and the previous parts show that
$2$
. Using Exercise 4.2, the fundamental domain in Figure 2 and the previous parts show that  $$ \begin{align*} \int_{\mathcal{M}_1} p(\Lambda,L) \thinspace d\widehat{\mu}(\Lambda)= L^2. \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_1} p(\Lambda,L) \thinspace d\widehat{\mu}(\Lambda)= L^2. \end{align*} $$
4.5 The cut and glue fibration
We now discuss a remarkable observation due to Mirzakhani regarding how the Weil–Petersson measure on certain quotients of Teichmüller space disintegrates along the fibers of natural projections over products of moduli spaces of lower complexity. This observation is nothing more than a simple consequence of Wolpert’s magic formula but its importance cannot be overstated.
For the rest of this discussion, we fix an integer
![]() $g \geq 2$
and a connected, oriented, closed surface
$g \geq 2$
and a connected, oriented, closed surface
![]() $S_g$
of genus g. Recall that
$S_g$
of genus g. Recall that
![]() $\mathrm {Mod}_g$
denotes the mapping class group of
$\mathrm {Mod}_g$
denotes the mapping class group of
![]() $S_g$
. Given a simple closed curve
$S_g$
. Given a simple closed curve
![]() $\alpha $
on
$\alpha $
on
![]() $S_{g}$
, denote by
$S_{g}$
, denote by
![]() $ \text {Stab}_0(\alpha ) \subseteq \text {Mod}_{g} $
the subgroup of mapping classes of
$ \text {Stab}_0(\alpha ) \subseteq \text {Mod}_{g} $
the subgroup of mapping classes of
![]() $S_{g}$
that fix
$S_{g}$
that fix
![]() $\alpha $
up to isotopy together with its orientations. Although
$\alpha $
up to isotopy together with its orientations. Although
![]() $\alpha $
is unoriented, it admits two possible orientations. A mapping class belongs to
$\alpha $
is unoriented, it admits two possible orientations. A mapping class belongs to
![]() $\text {Stab}_0(\alpha )$
if it sends each orientation of
$\text {Stab}_0(\alpha )$
if it sends each orientation of
![]() $\alpha $
back to itself. An ordered simple closed multi-curve on
$\alpha $
back to itself. An ordered simple closed multi-curve on
![]() $S_g$
is a tuple
$S_g$
is a tuple
![]() $\smash {\vec {\gamma } := (\gamma _i)_{i=1}^{k}}$
of pairwise disjoint, pairwise non-isotopic simple closed curves on
$\smash {\vec {\gamma } := (\gamma _i)_{i=1}^{k}}$
of pairwise disjoint, pairwise non-isotopic simple closed curves on
![]() $S_g$
. Given such a simple closed multi-curve on
$S_g$
. Given such a simple closed multi-curve on
![]() $S_{g}$
, denote
$S_{g}$
, denote
 $$ \begin{align*} \text{Stab}_0(\vec{\gamma}) := \bigcap_{i=1}^k \text{Stab}_0(\gamma_i) \subseteq \text{Mod}_{g}; \end{align*} $$
$$ \begin{align*} \text{Stab}_0(\vec{\gamma}) := \bigcap_{i=1}^k \text{Stab}_0(\gamma_i) \subseteq \text{Mod}_{g}; \end{align*} $$
considering this particular definition of stabilizer allows us to avoid possible inconsistencies in the formulas that could arise from the existence of extra symmetries for specific multi-curves.
For the rest of this discussion, we fix an ordered simple closed multi-curve
![]() $\vec {\gamma } := (\gamma _i)_{i=1}^k$
on
$\vec {\gamma } := (\gamma _i)_{i=1}^k$
on
![]() $S_{g}$
. Recall that
$S_{g}$
. Recall that
![]() $\mathcal {T}_g$
denotes the Teichmüller space of marked hyperbolic structures on
$\mathcal {T}_g$
denotes the Teichmüller space of marked hyperbolic structures on
![]() $S_g$
. The quotient
$S_g$
. The quotient
![]() $ \mathcal {T}_{g}/\text {Stab}_0(\vec {\gamma }) $
fibers naturally over a product of moduli spaces of surfaces with boundary of less complexity than
$ \mathcal {T}_{g}/\text {Stab}_0(\vec {\gamma }) $
fibers naturally over a product of moduli spaces of surfaces with boundary of less complexity than
![]() $S_{g}$
. This fibration, which we refer to as the cut and glue fibration of
$S_{g}$
. This fibration, which we refer to as the cut and glue fibration of
![]() $\mathcal {T}_{g}/\text {Stab}_0(\vec {\gamma })$
, will play a crucial role in our discussion of Mirzakhani’s integration formula. To describe this fibration in detail, we first introduce some notation.
$\mathcal {T}_{g}/\text {Stab}_0(\vec {\gamma })$
, will play a crucial role in our discussion of Mirzakhani’s integration formula. To describe this fibration in detail, we first introduce some notation.
Let
![]() $S_{g}(\vec {\gamma })$
be the potentially disconnected oriented surface with boundary obtained by cutting
$S_{g}(\vec {\gamma })$
be the potentially disconnected oriented surface with boundary obtained by cutting
![]() $S_{g}$
along the components of
$S_{g}$
along the components of
![]() $\vec {\gamma }$
. See Figure 14 for an example. Let
$\vec {\gamma }$
. See Figure 14 for an example. Let
![]() $c> 0$
be the number of components of
$c> 0$
be the number of components of
![]() $S_g(\vec {\gamma })$
. Fixing an orientation on each component of
$S_g(\vec {\gamma })$
. Fixing an orientation on each component of
![]() $\vec {\gamma }$
, we can keep track of which components of
$\vec {\gamma }$
, we can keep track of which components of
![]() $S_{g}(\vec {\gamma })$
lie to the left and to the right of each component of
$S_{g}(\vec {\gamma })$
lie to the left and to the right of each component of
![]() $\vec {\gamma }$
, so we can label the components of
$\vec {\gamma }$
, so we can label the components of
![]() $S_{g}(\vec {\gamma })$
in a consistent way, say
$S_{g}(\vec {\gamma })$
in a consistent way, say
![]() $\Sigma _j$
with
$\Sigma _j$
with
![]() $j \in \{1,\ldots ,c\}$
. As the components of
$j \in \{1,\ldots ,c\}$
. As the components of
![]() $\vec {\gamma }$
are labeled and oriented, this induces a labeling of the boundary components of each
$\vec {\gamma }$
are labeled and oriented, this induces a labeling of the boundary components of each
![]() $\Sigma _j$
. Let
$\Sigma _j$
. Let
![]() $g_j,b_j \geq 0$
with
$g_j,b_j \geq 0$
with
![]() $2 - 2g_j - b_j < 0$
be a pair of non-negative integers such that
$2 - 2g_j - b_j < 0$
be a pair of non-negative integers such that
![]() $\Sigma _j$
is homeomorphic to
$\Sigma _j$
is homeomorphic to
![]() $S_{g_j,b_j}$
. Fix a homeomorphism between this pair of surfaces respecting the labeling of their boundary components.
$S_{g_j,b_j}$
. Fix a homeomorphism between this pair of surfaces respecting the labeling of their boundary components.

Figure 14 Cutting a genus
![]() $2$
surface along a non-separating simple closed curve (colour online).
$2$
surface along a non-separating simple closed curve (colour online).
The base of the cut and glue fibration is the space
![]() $\Omega _{g}(\vec {\gamma })$
of pairs
$\Omega _{g}(\vec {\gamma })$
of pairs
![]() $(\mathbf {L},\mathbf {X})$
, where
$(\mathbf {L},\mathbf {X})$
, where
 $$ \begin{align*} \mathbf{L} := (\ell_i)_{i=1}^k \in (\mathbb {R}_{>0})^k,\\ \mathbf{X} := (X_j)_{j=1}^c \in \prod_{j=1}^c \mathcal{M}_{g_j,b_j}(\mathbf{L}_j), \end{align*} $$
$$ \begin{align*} \mathbf{L} := (\ell_i)_{i=1}^k \in (\mathbb {R}_{>0})^k,\\ \mathbf{X} := (X_j)_{j=1}^c \in \prod_{j=1}^c \mathcal{M}_{g_j,b_j}(\mathbf{L}_j), \end{align*} $$
such that
![]() $\mathbf {L}_j \in (\mathbb {R}_{>0})^{b_j}$
is defined using the vector
$\mathbf {L}_j \in (\mathbb {R}_{>0})^{b_j}$
is defined using the vector
![]() $\mathbf {L} := (\ell _i)_{i=1}^k \in (\mathbb {R}_{>0})^k$
and the correspondence between the labeling of the boundary components of
$\mathbf {L} := (\ell _i)_{i=1}^k \in (\mathbb {R}_{>0})^k$
and the correspondence between the labeling of the boundary components of
![]() $\Sigma _j$
and the labeling of the components of
$\Sigma _j$
and the labeling of the components of
![]() $\vec {\gamma }$
.
$\vec {\gamma }$
.
An ordered simple closed multi-geodesic
![]() $\alpha := (\alpha _i)_{i=1}^k$
on a hyperbolic surface X is a tuple of pairwise disjoint simple closed geodesics on X. Every ordered simple closed multi-geodesic is in particular an ordered simple closed multi-curve. Two ordered simple closed multi-curves on homeomorphic surfaces are said to have the same topological type if there exists a homeomorphism between the surfaces mapping one simple closed multi-curve to the other respecting their labelings. Recall that
$\alpha := (\alpha _i)_{i=1}^k$
on a hyperbolic surface X is a tuple of pairwise disjoint simple closed geodesics on X. Every ordered simple closed multi-geodesic is in particular an ordered simple closed multi-curve. Two ordered simple closed multi-curves on homeomorphic surfaces are said to have the same topological type if there exists a homeomorphism between the surfaces mapping one simple closed multi-curve to the other respecting their labelings. Recall that
![]() $\mathcal {M}_g$
denotes the moduli space of genus g hyperbolic surfaces. The following exercise will play a crucial role in our description of the cut and glue fibration.
$\mathcal {M}_g$
denotes the moduli space of genus g hyperbolic surfaces. The following exercise will play a crucial role in our description of the cut and glue fibration.
Exercise 4.4. Show there exists a one-to-one correspondence between points in the quotient space
![]() $\mathcal {T}_{g} /\text {Stab}_0(\vec {\gamma })$
and pairs
$\mathcal {T}_{g} /\text {Stab}_0(\vec {\gamma })$
and pairs
![]() $(X,\vec {\alpha })$
, where
$(X,\vec {\alpha })$
, where
![]() $X \in \mathcal {M}_{g}$
is a genus g hyperbolic surface and
$X \in \mathcal {M}_{g}$
is a genus g hyperbolic surface and
![]() $\vec {\alpha } := (\alpha _i)_{i=1}^k$
is an ordered simple closed multi-geodesic on X of the same topological type as
$\vec {\alpha } := (\alpha _i)_{i=1}^k$
is an ordered simple closed multi-geodesic on X of the same topological type as
![]() $\vec {\gamma }$
with a choice of orientation on each of its components, modulo the equivalence relation
$\vec {\gamma }$
with a choice of orientation on each of its components, modulo the equivalence relation
![]() $(X',\vec {\alpha }') \sim (X",\vec {\alpha }")$
if and only if there exists an orientation-preserving isometry
$(X',\vec {\alpha }') \sim (X",\vec {\alpha }")$
if and only if there exists an orientation-preserving isometry
![]() $I \colon X' \to X"$
sending the components of
$I \colon X' \to X"$
sending the components of
![]() $\vec {\alpha }'$
to the components of
$\vec {\alpha }'$
to the components of
![]() $\vec {\alpha }"$
respecting their labelings and orientations.
$\vec {\alpha }"$
respecting their labelings and orientations.
Consider the identification of the quotient space
![]() $\mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma })$
provided by Exercise 4.4. The cut and glue fibration of
$\mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma })$
provided by Exercise 4.4. The cut and glue fibration of
![]() $\mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma })$
is the map
$\mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma })$
is the map
![]() $\Psi \colon \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma }) \to \Omega _{g,n}(\vec {\gamma })$
which to every equivalence class
$\Psi \colon \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma }) \to \Omega _{g,n}(\vec {\gamma })$
which to every equivalence class
![]() $(X,\vec {\alpha }) \in \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma })$
assigns the pair
$(X,\vec {\alpha }) \in \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma })$
assigns the pair
![]() $(\mathbf {L},\mathbf {X}) \in \Omega _g(\vec {\gamma })$
given by
$(\mathbf {L},\mathbf {X}) \in \Omega _g(\vec {\gamma })$
given by
where
![]() $X(\vec {\alpha })_j \in \mathcal {M}_{g_j,b_j}(\mathbf {L}_j)$
is the jth component, according to the labeling and orientation of the components of
$X(\vec {\alpha })_j \in \mathcal {M}_{g_j,b_j}(\mathbf {L}_j)$
is the jth component, according to the labeling and orientation of the components of
![]() $\vec {\alpha }$
, of the hyperbolic surface with geodesic boundary components obtained by cutting X along the components of
$\vec {\alpha }$
, of the hyperbolic surface with geodesic boundary components obtained by cutting X along the components of
![]() $\vec {\alpha }$
. The fiber
$\vec {\alpha }$
. The fiber
![]() $\Psi ^{-1}(\mathbf {X},\mathbf {L})$
above any pair
$\Psi ^{-1}(\mathbf {X},\mathbf {L})$
above any pair
![]() $(\mathbf {L}, \mathbf {X}) \in \Omega _{g}(\vec {\gamma })$
is given by all possible ways of gluing the components of
$(\mathbf {L}, \mathbf {X}) \in \Omega _{g}(\vec {\gamma })$
is given by all possible ways of gluing the components of
![]() $\smash {\mathbf {X}:=(X_j)_{j=1}^c}$
along their boundaries respecting the labelings. Given any point
$\smash {\mathbf {X}:=(X_j)_{j=1}^c}$
along their boundaries respecting the labelings. Given any point
![]() $(X,\vec {\alpha }) \in \Psi ^{-1}(\mathbf {X},\mathbf {L})$
, the whole fiber
$(X,\vec {\alpha }) \in \Psi ^{-1}(\mathbf {X},\mathbf {L})$
, the whole fiber
![]() $\Psi ^{-1}(\mathbf {X},\mathbf {L})$
can be recovered by considering all possible Fenchel–Nielsen twists of X along the components of
$\Psi ^{-1}(\mathbf {X},\mathbf {L})$
can be recovered by considering all possible Fenchel–Nielsen twists of X along the components of
![]() $\vec {\alpha }$
.
$\vec {\alpha }$
.
Remark 4.5. Notice that, because of Exercise 3.3, Fenchel–Nielsen coordinates modulo Dehn twists along the components of the corresponding pair of pants decomposition are an instance of the cut and glue fibration; the base of the fibration is the positive orthant of possible cuff lengths.
Consider a point
![]() $(\mathbf {L},\mathbf {X}) \in \Omega _{g}(\vec {\gamma })$
on the base of the cut and glue fibration. Let
$(\mathbf {L},\mathbf {X}) \in \Omega _{g}(\vec {\gamma })$
on the base of the cut and glue fibration. Let
![]() $(X,\vec {\alpha }) \in \Psi ^{-1}(\mathbf {X},\mathbf {L})$
with
$(X,\vec {\alpha }) \in \Psi ^{-1}(\mathbf {X},\mathbf {L})$
with
![]() $\vec {\alpha } := (\alpha _i)_{i=1}^k$
. The fiber
$\vec {\alpha } := (\alpha _i)_{i=1}^k$
. The fiber
![]() $\Psi ^{-1}(\mathbf {X},\mathbf {L})$
supports well-defined
$\Psi ^{-1}(\mathbf {X},\mathbf {L})$
supports well-defined
![]() $1$
-forms
$1$
-forms
![]() $d\tau _{\alpha _i}$
that measure the infinitesimal Fenchel–Nielsen twists along the components of
$d\tau _{\alpha _i}$
that measure the infinitesimal Fenchel–Nielsen twists along the components of
![]() $\vec {\alpha }$
. Wedging these
$\vec {\alpha }$
. Wedging these
![]() $1$
-forms yields a natural volume form on
$1$
-forms yields a natural volume form on
![]() $\Psi ^{-1}(\mathbf {X},\mathbf {L})$
. For every set of lengths
$\Psi ^{-1}(\mathbf {X},\mathbf {L})$
. For every set of lengths
![]() $\mathbf {L} := (\ell _i)_{i=1}^k$
and for Weil–Petersson almost every
$\mathbf {L} := (\ell _i)_{i=1}^k$
and for Weil–Petersson almost every
![]() $\mathbf {X}$
, the total mass of the fiber
$\mathbf {X}$
, the total mass of the fiber
![]() $\Psi ^{-1}(\mathbf {X},\mathbf {L})$
with respect to this volume form is given by
$\Psi ^{-1}(\mathbf {X},\mathbf {L})$
with respect to this volume form is given by
where
![]() $\rho _{g}(\vec {\gamma })$
is the number of components of
$\rho _{g}(\vec {\gamma })$
is the number of components of
![]() $\vec {\gamma }$
that bound (on any of its sides) a component of
$\vec {\gamma }$
that bound (on any of its sides) a component of
![]() $S_{g}(\vec {\gamma })$
that is homeomorphic to a torus with one boundary component. We refer to pairs
$S_{g}(\vec {\gamma })$
that is homeomorphic to a torus with one boundary component. We refer to pairs
![]() $(\mathbf {L},\mathbf {X}) \in \Omega _{g}(\vec {\gamma })$
such that equation (4.2) holds as generic pairs. The factor
$(\mathbf {L},\mathbf {X}) \in \Omega _{g}(\vec {\gamma })$
such that equation (4.2) holds as generic pairs. The factor
![]() $2^{-\rho _{g}(\vec {\gamma })}$
reflects the observation that every hyperbolic torus with one geodesic boundary component has a non-trivial isometric involution preserving its boundary setwise; see Figure 15. A similar issue arises for higher genera hyperbolic surfaces with extra symmetries, and hence the need to impose the Weil–Petersson almost every condition on
$2^{-\rho _{g}(\vec {\gamma })}$
reflects the observation that every hyperbolic torus with one geodesic boundary component has a non-trivial isometric involution preserving its boundary setwise; see Figure 15. A similar issue arises for higher genera hyperbolic surfaces with extra symmetries, and hence the need to impose the Weil–Petersson almost every condition on
![]() $\mathbf {X}$
in equation (4.2).
$\mathbf {X}$
in equation (4.2).

Figure 15 The isometric involution of a torus with one boundary component (colour online).
Denote by
![]() $\mu _{\mathrm {wp}}$
the Weil–Petersson measure on
$\mu _{\mathrm {wp}}$
the Weil–Petersson measure on
![]() $\mathcal {T}_{g}$
and by
$\mathcal {T}_{g}$
and by
![]() $\widetilde {\mu }_{\mathrm {wp}}$
the local pushforward of
$\widetilde {\mu }_{\mathrm {wp}}$
the local pushforward of
![]() $\mu _{\mathrm {wp}}$
to
$\mu _{\mathrm {wp}}$
to
![]() $\mathcal {T}_g/\mathrm {Stab}_0(\vec {\gamma })$
. It follows from Wolpert’s magic formula, that is, from equations (3.1) and (4.1), that
$\mathcal {T}_g/\mathrm {Stab}_0(\vec {\gamma })$
. It follows from Wolpert’s magic formula, that is, from equations (3.1) and (4.1), that
![]() $\widetilde {\mu }_{\mathrm {wp}}$
can be disintegrated along the fibers of the cut and glue fibration
$\widetilde {\mu }_{\mathrm {wp}}$
can be disintegrated along the fibers of the cut and glue fibration
![]() $\Psi \colon \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma }) \to \Omega _{g,n}(\vec {\gamma })$
as
$\Psi \colon \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma }) \to \Omega _{g,n}(\vec {\gamma })$
as
 $$ \begin{align*} \widetilde{\mu}_{\mathrm{wp}} = \sigma_g(\vec{\gamma}) \cdot \prod_{i=1}^k d\tau_{\alpha_i} \otimes \prod_{i=1}^c \widehat{\mu}_{\mathrm{wp}}^j \otimes \prod_{i=1}^k d\ell_i, \end{align*} $$
$$ \begin{align*} \widetilde{\mu}_{\mathrm{wp}} = \sigma_g(\vec{\gamma}) \cdot \prod_{i=1}^k d\tau_{\alpha_i} \otimes \prod_{i=1}^c \widehat{\mu}_{\mathrm{wp}}^j \otimes \prod_{i=1}^k d\ell_i, \end{align*} $$
where
![]() $\widehat {\mu }_{\text {wp}}^j$
denotes the Weil–Petersson measure on
$\widehat {\mu }_{\text {wp}}^j$
denotes the Weil–Petersson measure on
![]() $\mathcal {M}_{g_j,b_j}(\mathbf {L}_j)$
and
$\mathcal {M}_{g_j,b_j}(\mathbf {L}_j)$
and
![]() $\sigma _g(\vec {\gamma }) \colon \mathcal {T}_g/\mathrm {Stab}_0(\vec {\gamma }) \to \mathbf {Q}_{>0}$
is the function with non-negative rational values that records the discrepancy between the stabilizer factors, that is, the factors
$\sigma _g(\vec {\gamma }) \colon \mathcal {T}_g/\mathrm {Stab}_0(\vec {\gamma }) \to \mathbf {Q}_{>0}$
is the function with non-negative rational values that records the discrepancy between the stabilizer factors, that is, the factors
![]() $|\Gamma |$
in equation (3.2), of the measure
$|\Gamma |$
in equation (3.2), of the measure
![]() $\widetilde {\mu }_{\mathrm {wp}}$
and the product of measures
$\widetilde {\mu }_{\mathrm {wp}}$
and the product of measures
![]() $\prod _{i=1}^c \widehat {\mu }_{\mathrm {wp}}^j$
. One can show that the function
$\prod _{i=1}^c \widehat {\mu }_{\mathrm {wp}}^j$
. One can show that the function
![]() $\sigma _g(\vec {\gamma })$
is almost everywhere constant with respect to
$\sigma _g(\vec {\gamma })$
is almost everywhere constant with respect to
![]() $\widetilde {\mu }_{\mathrm {wp}}$
and is given by
$\widetilde {\mu }_{\mathrm {wp}}$
and is given by
 $$ \begin{align*} \sigma_{g}(\vec{\gamma}) := \frac{\prod_{j=1}^c |K_{g_j,b_j}|}{|\text{Stab}_0(\vec{\gamma})\cap K_{g}|}, \end{align*} $$
$$ \begin{align*} \sigma_{g}(\vec{\gamma}) := \frac{\prod_{j=1}^c |K_{g_j,b_j}|}{|\text{Stab}_0(\vec{\gamma})\cap K_{g}|}, \end{align*} $$
where
![]() $K_{g_j,b_j} \triangleleft \text {Mod}_{g_j,b_j}$
is the kernel of the mapping class group action on
$K_{g_j,b_j} \triangleleft \text {Mod}_{g_j,b_j}$
is the kernel of the mapping class group action on
![]() $\mathcal {T}_{g_j,b_j}$
and
$\mathcal {T}_{g_j,b_j}$
and
![]() $K_{g} \triangleleft \text {Mod}_{g}$
is the kernel of the mapping class group action on
$K_{g} \triangleleft \text {Mod}_{g}$
is the kernel of the mapping class group action on
![]() $\mathcal {T}_{g}$
. Indeed,
$\mathcal {T}_{g}$
. Indeed,
![]() $\widehat {\mu }_{\mathrm {wp}}^j$
almost every hyperbolic surface in
$\widehat {\mu }_{\mathrm {wp}}^j$
almost every hyperbolic surface in
![]() $\mathcal {M}_{g_j,b_j}(\mathbf {L})$
has
$\mathcal {M}_{g_j,b_j}(\mathbf {L})$
has
![]() $|K_{g_j,b_j}|$
automorphisms and analogously for elements of
$|K_{g_j,b_j}|$
automorphisms and analogously for elements of
![]() $\mathcal {T}_g/\mathrm {Stab}_0(\vec {\gamma })$
. For example, if
$\mathcal {T}_g/\mathrm {Stab}_0(\vec {\gamma })$
. For example, if
![]() $g =2$
and
$g =2$
and
![]() $\vec {\gamma }$
is a separating simple closed curve on
$\vec {\gamma }$
is a separating simple closed curve on
![]() $S_{2}$
, then
$S_{2}$
, then
![]() $\sigma _{2}(\vec {\gamma }) = 4/2 = 2$
. In general,
$\sigma _{2}(\vec {\gamma }) = 4/2 = 2$
. In general,
 $$ \begin{align*} |K_{g,b}| = \begin{cases} 4 & \text{if } (g,b) = (0,4), \\ 2 & \text{if } (g,b) \in \{(1,1),(1,2),(2,0)\}, \\ 1 & \text{if } (g,b) \notin \{(0,4),(1,1),(1,2),(2,0)\}.\\ \end{cases}\! \end{align*} $$
$$ \begin{align*} |K_{g,b}| = \begin{cases} 4 & \text{if } (g,b) = (0,4), \\ 2 & \text{if } (g,b) \in \{(1,1),(1,2),(2,0)\}, \\ 1 & \text{if } (g,b) \notin \{(0,4),(1,1),(1,2),(2,0)\}.\\ \end{cases}\! \end{align*} $$
Let us record the most important conclusions of the discussion above in the following theorem.
Theorem 4.6. The Weil–Petersson measure
![]() $\widetilde {\mu }_{\mathrm {wp}}$
on
$\widetilde {\mu }_{\mathrm {wp}}$
on
![]() $\mathcal {T}_{g} /\text {Stab}_0(\vec {\gamma })$
can be disintegrated along the fibers of the cut and glue fibration
$\mathcal {T}_{g} /\text {Stab}_0(\vec {\gamma })$
can be disintegrated along the fibers of the cut and glue fibration
![]() $\Psi \colon \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma }) \to \Omega _{g,n}(\vec {\gamma })$
in the following way:
$\Psi \colon \mathcal {T}_{g,n} /\text {Stab}_0(\vec {\gamma }) \to \Omega _{g,n}(\vec {\gamma })$
in the following way:
 $$ \begin{align*} \widetilde{\mu}_{\mathrm{wp}} = \sigma_g(\vec{\gamma}) \cdot \prod_{i=1}^k d\tau_{\alpha_i} \otimes \prod_{i=1}^c \widehat{\mu}_{\mathrm{wp}}^j \otimes \prod_{i=1}^k d\ell_i. \end{align*} $$
$$ \begin{align*} \widetilde{\mu}_{\mathrm{wp}} = \sigma_g(\vec{\gamma}) \cdot \prod_{i=1}^k d\tau_{\alpha_i} \otimes \prod_{i=1}^c \widehat{\mu}_{\mathrm{wp}}^j \otimes \prod_{i=1}^k d\ell_i. \end{align*} $$
Generically, the volume of the fiber
![]() $\Psi ^{-1}(\mathbf {X},\mathbf {L})$
above a
$\Psi ^{-1}(\mathbf {X},\mathbf {L})$
above a
![]() $(\mathbf {L},\mathbf {X}) \in \Omega _{g,n}(\vec {\gamma })$
with
$(\mathbf {L},\mathbf {X}) \in \Omega _{g,n}(\vec {\gamma })$
with
![]() $\mathbf {L} := (\ell _i)_{i=1}^k$
is equal to
$\mathbf {L} := (\ell _i)_{i=1}^k$
is equal to
4.6 Mirzakhani’s integration formula
We are now ready to discuss Mirzakhani’s integration formula. Let
![]() $\vec {\gamma } := (\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
$\vec {\gamma } := (\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
![]() $S_g$
. Consider the stabilizer
$S_g$
. Consider the stabilizer
 $$ \begin{align*} \mathrm{Stab}(\vec{\gamma}) := \bigcap_{i=1}^k \mathrm{Stab}(\gamma_i) \subseteq \mathrm{Mod}_g. \end{align*} $$
$$ \begin{align*} \mathrm{Stab}(\vec{\gamma}) := \bigcap_{i=1}^k \mathrm{Stab}(\gamma_i) \subseteq \mathrm{Mod}_g. \end{align*} $$
Notice that
![]() $\mathrm {Stab}_0(\vec {\gamma })$
is a finite index subgroup of
$\mathrm {Stab}_0(\vec {\gamma })$
is a finite index subgroup of
![]() $\mathrm {Stab}(\vec {\gamma })$
. Let
$\mathrm {Stab}(\vec {\gamma })$
. Let
![]() $c> 0$
and
$c> 0$
and
![]() $g_j,b_j \geq 0$
with
$g_j,b_j \geq 0$
with
![]() $j \in \{1, \ldots , c\}$
be as above. Consider the total Weil–Petersson volumes
$j \in \{1, \ldots , c\}$
be as above. Consider the total Weil–Petersson volumes
of the moduli spaces
![]() $\mathcal {M}_{g_j,b_j}(\mathbf {x}_j)$
as functions of the boundary lengths
$\mathcal {M}_{g_j,b_j}(\mathbf {x}_j)$
as functions of the boundary lengths
![]() $\mathbf {x}_j \in \mathbb {R}_+^{b_j}$
. Recall the definitions of the constants
$\mathbf {x}_j \in \mathbb {R}_+^{b_j}$
. Recall the definitions of the constants
![]() $\rho _{g}(\vec {\gamma }) \in \mathbb{N}$
and
$\rho _{g}(\vec {\gamma }) \in \mathbb{N}$
and
![]() $\sigma _g(\vec {\gamma }) \in \mathbf {Q}_{>0}$
introduced above. Consider the measurable function
$\sigma _g(\vec {\gamma }) \in \mathbf {Q}_{>0}$
introduced above. Consider the measurable function
![]() $V_g(\vec {\gamma },\cdot ) \colon \mathbb {R}_+^k \to \mathbb {R}_+$
which, to every vector
$V_g(\vec {\gamma },\cdot ) \colon \mathbb {R}_+^k \to \mathbb {R}_+$
which, to every vector
![]() $\mathbf {x} := (x_i)_{i=1}^k$
with positive entries, assigns the value
$\mathbf {x} := (x_i)_{i=1}^k$
with positive entries, assigns the value
 $$ \begin{align} V_g(\vec{\gamma},\mathbf{x}) := \frac{\sigma_g(\vec{\gamma}) \cdot 2^{-\rho_g(\vec{\gamma})}}{[\mathrm{Stab}(\vec{\gamma}):\mathrm{Stab}_0(\vec{\gamma})]} \cdot \prod_{j=1}^c V_{g_j,b_j}(\mathbf{x}_j), \end{align} $$
$$ \begin{align} V_g(\vec{\gamma},\mathbf{x}) := \frac{\sigma_g(\vec{\gamma}) \cdot 2^{-\rho_g(\vec{\gamma})}}{[\mathrm{Stab}(\vec{\gamma}):\mathrm{Stab}_0(\vec{\gamma})]} \cdot \prod_{j=1}^c V_{g_j,b_j}(\mathbf{x}_j), \end{align} $$
where the vector
![]() $\mathbf {x}_j \in \mathbb {R}_+^{b_j}$
is defined using the correspondence between the components of
$\mathbf {x}_j \in \mathbb {R}_+^{b_j}$
is defined using the correspondence between the components of
![]() $\vec {\gamma }$
and the boundary components of
$\vec {\gamma }$
and the boundary components of
![]() $S_{g_j,b_j}$
. By Theorem 4.1,
$S_{g_j,b_j}$
. By Theorem 4.1,
![]() $V_g(\vec {\gamma },\mathbf {x})$
is a polynomial on the
$V_g(\vec {\gamma },\mathbf {x})$
is a polynomial on the
![]() $\mathbf {x}$
variables.
$\mathbf {x}$
variables.
Let
![]() $f \colon \smash {\mathbb {R}_+^k} \to \mathbb {R}$
be a non-negative, measurable function. Given
$f \colon \smash {\mathbb {R}_+^k} \to \mathbb {R}$
be a non-negative, measurable function. Given
![]() $X \in \mathcal {T}_g$
and an ordered simple closed multi-curve
$X \in \mathcal {T}_g$
and an ordered simple closed multi-curve
![]() $\smash {\vec {\alpha } := (\alpha _i)_{i=1}^k}$
on
$\smash {\vec {\alpha } := (\alpha _i)_{i=1}^k}$
on
![]() $S_g$
, denote
$S_g$
, denote
![]() $\smash {\ell _{\vec {\alpha }}}(X) := (\ell _{\alpha _i}(X))_{i=1}^k \in \mathbb {R}_+^k$
. Consider the non-negative, measurable function
$\smash {\ell _{\vec {\alpha }}}(X) := (\ell _{\alpha _i}(X))_{i=1}^k \in \mathbb {R}_+^k$
. Consider the non-negative, measurable function
![]() $f_{\vec {\gamma }} \colon \mathcal {T}_g \to \mathbb {R}$
which, to every
$f_{\vec {\gamma }} \colon \mathcal {T}_g \to \mathbb {R}$
which, to every
![]() $X \in \mathcal {T}_g$
, assigns the value
$X \in \mathcal {T}_g$
, assigns the value
 $$ \begin{align*} f_{\vec{\gamma}}(X) := \sum_{\vec{\alpha} \in \mathrm{Mod}_g \cdot \vec{\gamma}} f(\smash{\ell_{\vec{\alpha}}}(X)). \end{align*} $$
$$ \begin{align*} f_{\vec{\gamma}}(X) := \sum_{\vec{\alpha} \in \mathrm{Mod}_g \cdot \vec{\gamma}} f(\smash{\ell_{\vec{\alpha}}}(X)). \end{align*} $$
This function is clearly invariant with respect to the action of
![]() $\mathrm {Mod}_g$
on
$\mathrm {Mod}_g$
on
![]() $\mathcal {T}_g$
. Denote by
$\mathcal {T}_g$
. Denote by
![]() $\smash {\widehat {f}}_{\vec {\gamma }} \colon \mathcal {M}_g \to \mathbb {R}$
the corresponding non-negative, measurable function induced on moduli space. Denote by
$\smash {\widehat {f}}_{\vec {\gamma }} \colon \mathcal {M}_g \to \mathbb {R}$
the corresponding non-negative, measurable function induced on moduli space. Denote by
![]() $\widehat {\mu }_{\mathrm {wp}}$
the Weil–Petersson measure on
$\widehat {\mu }_{\mathrm {wp}}$
the Weil–Petersson measure on
![]() $\mathcal {M}_g$
. On
$\mathcal {M}_g$
. On
![]() $\smash {\mathbb {R}_+^k}$
, consider the standard coordinate system
$\smash {\mathbb {R}_+^k}$
, consider the standard coordinate system
![]() $\mathbf {x} := \smash {(x_i)_{i=1}^k}$
and the Lebesgue class measure
$\mathbf {x} := \smash {(x_i)_{i=1}^k}$
and the Lebesgue class measure
![]() $\mathbf {x} \cdot d\mathbf {x} := x_1 \cdots x_k \cdot dx_1 \cdots dx_k$
. The following exercise corresponds to Mirzakhani’s integration formula [Reference MirzakhaniMir08b, Theorem 4.1].
$\mathbf {x} \cdot d\mathbf {x} := x_1 \cdots x_k \cdot dx_1 \cdots dx_k$
. The following exercise corresponds to Mirzakhani’s integration formula [Reference MirzakhaniMir08b, Theorem 4.1].
Exercise 4.7. Let
![]() $\vec {\gamma } := (\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
$\vec {\gamma } := (\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
![]() $S_g$
. Using Exercise 4.2 and Theorem 4.6, show that the following integration formula holds:
$S_g$
. Using Exercise 4.2 and Theorem 4.6, show that the following integration formula holds:
 $$ \begin{align*} \int_{\mathcal{M}_g} \widehat{f}_{\vec{\gamma}}(X) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = \int_{\mathbb {R}_+^k} f(\mathbf{x}) \cdot V_g(\vec{\gamma},\mathbf{x}) \cdot \mathbf{x} \cdot d\mathbf{x}. \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_g} \widehat{f}_{\vec{\gamma}}(X) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = \int_{\mathbb {R}_+^k} f(\mathbf{x}) \cdot V_g(\vec{\gamma},\mathbf{x}) \cdot \mathbf{x} \cdot d\mathbf{x}. \end{align*} $$
4.7 McShane’s identity
We now sketch a proof of Theorem 4.1 for the case of tori with one boundary component, that is, for the case
![]() $g=1$
and
$g=1$
and
![]() $b=1$
. For the rest of this discussion, we fix a torus with one boundary component
$b=1$
. For the rest of this discussion, we fix a torus with one boundary component
![]() $S_{1,1}$
and a parameter
$S_{1,1}$
and a parameter
![]() $L> 0$
. To compute the total Weil–Petersson volume
$L> 0$
. To compute the total Weil–Petersson volume
![]() $V_{1,1}(L) := \widehat {\mu }_{\mathrm {wp}}(\mathcal {M}_{1,1}(L))$
, one could recall
$V_{1,1}(L) := \widehat {\mu }_{\mathrm {wp}}(\mathcal {M}_{1,1}(L))$
, one could recall
![]() $\mathcal {M}_{1,1}(L) := \mathcal {T}_{1,1}(L)/ \mathrm {Mod}_{1,1}$
and try to find a fundamental domain for the action of
$\mathcal {M}_{1,1}(L) := \mathcal {T}_{1,1}(L)/ \mathrm {Mod}_{1,1}$
and try to find a fundamental domain for the action of
![]() $\mathrm {Mod}_{1,1}$
on
$\mathrm {Mod}_{1,1}$
on
![]() $\mathcal {T}_{1,1}(L)$
that can be described explicitly in Fenchel–Nielsen coordinates. This happens to be quite a formidable task. In the absence of such a fundamental domain, we consider a different approach that relies on Mirzakhani’s integration formula.
$\mathcal {T}_{1,1}(L)$
that can be described explicitly in Fenchel–Nielsen coordinates. This happens to be quite a formidable task. In the absence of such a fundamental domain, we consider a different approach that relies on Mirzakhani’s integration formula.
For the rest of this discussion, we fix a simple closed curve
![]() $\gamma $
on
$\gamma $
on
![]() $S_{1,1}$
. Let
$S_{1,1}$
. Let
![]() $f \colon \mathbb {R}_+ \to \mathbb {R}$
be a non-negative measurable function. Just as in the case of closed surfaces, consider the non-negative, measurable transform
$f \colon \mathbb {R}_+ \to \mathbb {R}$
be a non-negative measurable function. Just as in the case of closed surfaces, consider the non-negative, measurable transform
![]() $\smash {\widehat {f}_\gamma } \colon \mathcal {M}_{1,1}(L) \to \mathbb {R}$
which, to every
$\smash {\widehat {f}_\gamma } \colon \mathcal {M}_{1,1}(L) \to \mathbb {R}$
which, to every
![]() $X \in \mathcal {M}_{1,1}(L)$
, assigns the value
$X \in \mathcal {M}_{1,1}(L)$
, assigns the value
 $$ \begin{align*} \smash{\widehat{f}_\gamma}(X) = \sum_{\alpha \in \mathrm{Mod}_{1,1} \cdot \gamma} f(\ell_{\gamma}(X)). \end{align*} $$
$$ \begin{align*} \smash{\widehat{f}_\gamma}(X) = \sum_{\alpha \in \mathrm{Mod}_{1,1} \cdot \gamma} f(\ell_{\gamma}(X)). \end{align*} $$
An analog of Mirzakhani’s integration formula in Exercise 4.7 also holds in this setting. Our immediate goal is to find a non-negative, measurable function
![]() $f \colon \mathbb {R}_+ \to \mathbb {R}$
for which the transform
$f \colon \mathbb {R}_+ \to \mathbb {R}$
for which the transform
![]() $\smash {\widehat {f}_\gamma } \colon \mathcal {M}_{1,1}(L) \to \mathbb {R}$
is equal to a constant
$\smash {\widehat {f}_\gamma } \colon \mathcal {M}_{1,1}(L) \to \mathbb {R}$
is equal to a constant
![]() $c(L)> 0$
. Indeed, for such a function, we would have
$c(L)> 0$
. Indeed, for such a function, we would have
 $$ \begin{align} c(L) \cdot \widehat{\mu}_{\mathrm{wp}}(\mathcal{M}_{1,1}(L)) = \int_{\mathcal{M}_{1,1}(L)} \widehat{f}_\gamma(X) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = \frac{1}{2} \cdot \int_{\mathbb {R}_+}f(x) \cdot x \cdot dx. \end{align} $$
$$ \begin{align} c(L) \cdot \widehat{\mu}_{\mathrm{wp}}(\mathcal{M}_{1,1}(L)) = \int_{\mathcal{M}_{1,1}(L)} \widehat{f}_\gamma(X) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = \frac{1}{2} \cdot \int_{\mathbb {R}_+}f(x) \cdot x \cdot dx. \end{align} $$
Rearranging the terms in this equation would yield
 $$ \begin{align} V_{1,1}(L) := \widehat{\mu}_{\mathrm{wp}}(\mathcal{M}_{1,1}(L)) = \frac{1}{2 \cdot c(L)} \cdot \int_{\mathbb {R}_+}f(x) \cdot x \cdot dx. \end{align} $$
$$ \begin{align} V_{1,1}(L) := \widehat{\mu}_{\mathrm{wp}}(\mathcal{M}_{1,1}(L)) = \frac{1}{2 \cdot c(L)} \cdot \int_{\mathbb {R}_+}f(x) \cdot x \cdot dx. \end{align} $$
Finding a non-negative, measurable function
![]() $f \colon \mathbb {R}_+\hspace{-1pt} \to\hspace{-1pt} \mathbb {R}$
for which
$f \colon \mathbb {R}_+\hspace{-1pt} \to\hspace{-1pt} \mathbb {R}$
for which
![]() $\smash {\widehat {f}_\gamma } \colon \mathcal {M}_{1,1}(L)\hspace{-1pt} \to\hspace{-1pt} \mathbb {R}$
is constant is the content of McShane’s identity. Consider the function
$\smash {\widehat {f}_\gamma } \colon \mathcal {M}_{1,1}(L)\hspace{-1pt} \to\hspace{-1pt} \mathbb {R}$
is constant is the content of McShane’s identity. Consider the function
![]() $D \colon \mathbb {R}^3 \to \mathbb {R}$
given by
$D \colon \mathbb {R}^3 \to \mathbb {R}$
given by
 $$ \begin{align*} D(x,y,z) := 2 \log \bigg(\frac{e^{{x}/{2}} + e^{({y+z})/{2}}}{e^{-{x}/{2}} + e^{({y+z})/{2}}} \bigg). \end{align*} $$
$$ \begin{align*} D(x,y,z) := 2 \log \bigg(\frac{e^{{x}/{2}} + e^{({y+z})/{2}}}{e^{-{x}/{2}} + e^{({y+z})/{2}}} \bigg). \end{align*} $$
Theorem 4.8. [Reference McShaneMcS91]
Let
![]() $\gamma $
be a simple closed curve on
$\gamma $
be a simple closed curve on
![]() $S_{1,1}$
and
$S_{1,1}$
and
![]() $L> 0$
. Then, for every
$L> 0$
. Then, for every
![]() $X \in \mathcal {M}_{1,1}(L)$
,
$X \in \mathcal {M}_{1,1}(L)$
,
 $$ \begin{align} \sum_{\alpha \in \mathrm{Mod}_{1,1} \cdot \gamma} D(L,\ell_{\alpha}(X),\ell_{\alpha}(X)) = L. \end{align} $$
$$ \begin{align} \sum_{\alpha \in \mathrm{Mod}_{1,1} \cdot \gamma} D(L,\ell_{\alpha}(X),\ell_{\alpha}(X)) = L. \end{align} $$
Let us give a quick rundown of the main ideas of the proof of Theorem 4.8. For this, we interpret the right-hand side of equation (4.6) as the length of the boundary component of
![]() $X \in \mathcal {M}_{1,1}(L)$
. For every point on this boundary component, we shoot a geodesic into X in the direction orthogonal to the boundary. Three things can happen at this stage. Either the geodesic remains in X at all times without intersecting itself, the geodesic exits X without intersecting itself, or the geodesic intersects itself. By the work of Birman and Series [Reference Birman and SeriesBS85], the first case only happens for a measure zero subset of points on the boundary. In each of the two other cases, we consider the simple closed curves
$X \in \mathcal {M}_{1,1}(L)$
. For every point on this boundary component, we shoot a geodesic into X in the direction orthogonal to the boundary. Three things can happen at this stage. Either the geodesic remains in X at all times without intersecting itself, the geodesic exits X without intersecting itself, or the geodesic intersects itself. By the work of Birman and Series [Reference Birman and SeriesBS85], the first case only happens for a measure zero subset of points on the boundary. In each of the two other cases, we consider the simple closed curves
![]() $\alpha $
described in Figure 16. Cutting X along the corresponding geodesic representatives yields a hyperbolic pair of pants with boundary lengths
$\alpha $
described in Figure 16. Cutting X along the corresponding geodesic representatives yields a hyperbolic pair of pants with boundary lengths
![]() $(L,\ell _\alpha (X),\ell _{\alpha }(X))$
. Using the rigidity of such pairs of pants, one can show that for points in exactly two arcs of the original boundary component whose lengths add up to
$(L,\ell _\alpha (X),\ell _{\alpha }(X))$
. Using the rigidity of such pairs of pants, one can show that for points in exactly two arcs of the original boundary component whose lengths add up to
![]() $D(L,\ell _\alpha (X),\ell _{\alpha }(X))$
, the corresponding orthogonal geodesics either intersect themselves or the original boundary component before exiting the pants. Putting these ideas together finishes the proof.
$D(L,\ell _\alpha (X),\ell _{\alpha }(X))$
, the corresponding orthogonal geodesics either intersect themselves or the original boundary component before exiting the pants. Putting these ideas together finishes the proof.
Exercise 4.9. Using equation (4.5) and Theorem 4.8 show that
Hint: To simplify the computations, differentiate equation (4.4) with respect to L instead of using equation (4.5) directly.

Figure 16 The geodesic shot orthogonal to the boundary (in blue) determines a simple closed curve (in green) which tightens to a simple closed geodesic (in red) (colour online).
In her thesis [Reference MirzakhaniMir04], Mirzakhani generalized Theorem 4.8 to arbitrary closed, orientable surfaces [Reference MirzakhaniMir07a, Theorem 1.3]. Using this generalization, Mirzakhani proved a recursive formula for the total Weil–Petersson volumes
![]() $V_{g,b}(\mathbf {L})$
[Reference MirzakhaniMir07a, §5]. Using this formula, she ultimately deduced Theorem 4.1. An alternative proof of Theorem 4.1 using symplectic reduction can also be found in Mirzakhani’s thesis [Reference MirzakhaniMir07b, Theorem 1.1]. An excellent reference for all these topics is Do’s survey [Reference DoDo13].
$V_{g,b}(\mathbf {L})$
[Reference MirzakhaniMir07a, §5]. Using this formula, she ultimately deduced Theorem 4.1. An alternative proof of Theorem 4.1 using symplectic reduction can also be found in Mirzakhani’s thesis [Reference MirzakhaniMir07b, Theorem 1.1]. An excellent reference for all these topics is Do’s survey [Reference DoDo13].
In subsequent discussions, we will use the following explicit volume polynomial:
Exercise 4.10. Recall the definition of the polynomials
![]() $V_g(\vec {\gamma },\mathbf {x})$
in equation (4.3). Let
$V_g(\vec {\gamma },\mathbf {x})$
in equation (4.3). Let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
be non-separating and separating simple closed curves on
$\gamma _2$
be non-separating and separating simple closed curves on
![]() $S_2$
, respectively. Using equations (4.7) and (4.8), show that
$S_2$
, respectively. Using equations (4.7) and (4.8), show that
5 Counting simple closed geodesics on hyperbolic surfaces
5.1 Outline of this section
In this section, we give a complete proof of Theorem 1.1, the main result of this survey. We follow the same approach as in the proof of Theorem 2.1, but use the vocabulary and tools introduced in §§3–4. More concretely, we reduce to the study of an appropriate family of counting measures whose limit points are investigated using ergodic theory and integration formulas. We encourage the reader to keep in mind the analogies described in Table 1 for the rest of this section.
5.2 Counting simple closed geodesics
Recall that Theorem 1.1, the main result of this survey, asserts that the number
![]() $s(X,L)$
of unoriented simple closed geodesics of length
$s(X,L)$
of unoriented simple closed geodesics of length
![]() $\leq L$
on an arbitrary closed, orientable hyperbolic surface X of genus
$\leq L$
on an arbitrary closed, orientable hyperbolic surface X of genus
![]() $g \geq 2$
is asymptotic as
$g \geq 2$
is asymptotic as
![]() $L \to \infty $
to a polynomial of degree
$L \to \infty $
to a polynomial of degree
![]() $6g-6$
on L. We aim to rewrite the counting function
$6g-6$
on L. We aim to rewrite the counting function
![]() $s(X,L)$
using the terminology introduced in previous sections; we refer the reader to §§3 and 4 for the notation that will be used throughout.
$s(X,L)$
using the terminology introduced in previous sections; we refer the reader to §§3 and 4 for the notation that will be used throughout.
For the rest of this section, we fix an integer
![]() $g \geq 2$
and a connected, oriented, closed surface
$g \geq 2$
and a connected, oriented, closed surface
![]() $S_g$
of genus g. We begin by considering the following combinatorial exercise; compare with Exercise 3.5.
$S_g$
of genus g. We begin by considering the following combinatorial exercise; compare with Exercise 3.5.
Exercise 5.1. Show there are only finitely many topological types of simple closed curves on
![]() $S_g$
. Can you give an exact formula for the number of such equivalence classes?
$S_g$
. Can you give an exact formula for the number of such equivalence classes?
Recall that if
![]() $\gamma $
is a simple closed curve on
$\gamma $
is a simple closed curve on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {T}_g$
is a marked hyperbolic structure on
$X \in \mathcal {T}_g$
is a marked hyperbolic structure on
![]() $S_g$
, then
$S_g$
, then
![]() $\ell _{\gamma }(X)> 0 $
denotes the length of the unique geodesic representative of
$\ell _{\gamma }(X)> 0 $
denotes the length of the unique geodesic representative of
![]() $\gamma $
with respect to X. Let
$\gamma $
with respect to X. Let
![]() $\gamma $
be a simple closed curve on
$\gamma $
be a simple closed curve on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {T}_g$
. For every
$X \in \mathcal {T}_g$
. For every
![]() $L> 0$
, consider the counting function
$L> 0$
, consider the counting function
As every free homotopy class of simple closed curves on
![]() $S_g$
has a unique geodesic representative with respect to X, this is exactly the number of unoriented simple closed geodesics on X of the same topological type as
$S_g$
has a unique geodesic representative with respect to X, this is exactly the number of unoriented simple closed geodesics on X of the same topological type as
![]() $\gamma $
and length
$\gamma $
and length
![]() $\leq L$
. Hence, we can decompose the counting function
$\leq L$
. Hence, we can decompose the counting function
![]() $s(X,L)$
as
$s(X,L)$
as
where
![]() $\gamma $
runs over all the finitely many different topological types of simple closed curves on
$\gamma $
runs over all the finitely many different topological types of simple closed curves on
![]() $S_g$
; see Exercise 5.1. Thus, it is enough for our purposes to study the asymptotics of
$S_g$
; see Exercise 5.1. Thus, it is enough for our purposes to study the asymptotics of
![]() $s(X,\gamma ,L)$
as
$s(X,\gamma ,L)$
as
![]() $L \to \infty $
.
$L \to \infty $
.
Motivated by this observation, we generalize the definition of the counting function
![]() $s(X,\gamma ,L)$
to general integral simple closed multi-curves on
$s(X,\gamma ,L)$
to general integral simple closed multi-curves on
![]() $S_g$
. Recall that if
$S_g$
. Recall that if
![]() $\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
is a simple closed multi-curve on
$\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
is a simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {T}_g$
, then
$X \in \mathcal {T}_g$
, then
![]() $\ell _{\alpha }(X) := \sum _{i=1} a_i \ell _{\alpha _i}(X)> 0$
. Let
$\ell _{\alpha }(X) := \sum _{i=1} a_i \ell _{\alpha _i}(X)> 0$
. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {T}_g$
. For every
$X \in \mathcal {T}_g$
. For every
![]() $L> 0$
, consider the counting function
$L> 0$
, consider the counting function
Notice the function
![]() $s(X,\gamma ,L)$
does not depend on the marking of
$s(X,\gamma ,L)$
does not depend on the marking of
![]() $X \in \mathcal {T}_g$
, but only on its underlying hyperbolic structure
$X \in \mathcal {T}_g$
, but only on its underlying hyperbolic structure
![]() $X \in \mathcal {M}_g$
. We aim to prove the following asymptotic estimate for the counting function
$X \in \mathcal {M}_g$
. We aim to prove the following asymptotic estimate for the counting function
![]() $s(X,\gamma ,L)$
. Theorem 1.1 will later be deduced as a direct consequence of this estimate.
$s(X,\gamma ,L)$
. Theorem 1.1 will later be deduced as a direct consequence of this estimate.
Theorem 5.2. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {M}_g$
. Then, there exists a constant
$X \in \mathcal {M}_g$
. Then, there exists a constant
![]() $n(X,\gamma )> 0$
depending only on the topological type of
$n(X,\gamma )> 0$
depending only on the topological type of
![]() $\gamma $
and the geometry of X such that the following asymptotic estimate holds as
$\gamma $
and the geometry of X such that the following asymptotic estimate holds as
![]() $L \to \infty $
,
$L \to \infty $
,
5.3 Counting measures on the space of measured geodesic laminations
Inspired by the case of lattices, to prove Theorem 5.2, we introduce appropriate families of counting measures. Recall that
![]() $\mathcal {ML}_g$
denotes the space of measured geodesic laminations on
$\mathcal {ML}_g$
denotes the space of measured geodesic laminations on
![]() $S_g$
, that is, the natural
$S_g$
, that is, the natural
![]() $6g-6$
dimensional completion of the set of simple closed multi-curves on
$6g-6$
dimensional completion of the set of simple closed multi-curves on
![]() $S_g$
. Let
$S_g$
. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
. For every
$S_g$
. For every
![]() $L> 0$
, consider the counting measure on
$L> 0$
, consider the counting measure on
![]() $\mathcal {ML}_g$
given by
$\mathcal {ML}_g$
given by
 $$ \begin{align} \mu^\gamma_L := \frac{1}{L^{6g-6}} \cdot \sum_{\alpha \in \mathrm{Mod}_g \cdot \gamma} \delta_{{1}/{L} \cdot \alpha}. \end{align} $$
$$ \begin{align} \mu^\gamma_L := \frac{1}{L^{6g-6}} \cdot \sum_{\alpha \in \mathrm{Mod}_g \cdot \gamma} \delta_{{1}/{L} \cdot \alpha}. \end{align} $$
Recall that
![]() $\ell _\unicode{x3bb} (X)> 0$
denotes the length of a measured geodesic lamination
$\ell _\unicode{x3bb} (X)> 0$
denotes the length of a measured geodesic lamination
![]() $\unicode{x3bb} \in \mathcal {ML}_g$
with respect to a marked hyperbolic structure
$\unicode{x3bb} \in \mathcal {ML}_g$
with respect to a marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
. Given
$X \in \mathcal {T}_g$
. Given
![]() $X \in \mathcal {T}_g$
, consider the set
$X \in \mathcal {T}_g$
, consider the set
This set depends on the marking of
![]() $X \in \mathcal {T}_g$
. Directly from the definitions, we see that, for every
$X \in \mathcal {T}_g$
. Directly from the definitions, we see that, for every
![]() $L> 0$
,
$L> 0$
,
This reduces the original problem of proving an asymptotic estimate for the counting function
![]() $s(X,\gamma ,L)$
to the problem of understanding the behavior as
$s(X,\gamma ,L)$
to the problem of understanding the behavior as
![]() $L \to \infty $
of the sequence of counting measures
$L \to \infty $
of the sequence of counting measures
![]() $(\smash {\mu ^\gamma _L})_{L> 0}$
.
$(\smash {\mu ^\gamma _L})_{L> 0}$
.
5.4 Ergodicity of the mapping class group action
To study the asymptotic behavior of the sequence of counting measures
![]() $(\smash {\mu ^\gamma _L})_{L> 0}$
, we use the dynamics of the action of the mapping class group on
$(\smash {\mu ^\gamma _L})_{L> 0}$
, we use the dynamics of the action of the mapping class group on
![]() $\mathcal {ML}_g$
. Recall the definition of the Thurston measure
$\mathcal {ML}_g$
. Recall the definition of the Thurston measure
![]() $\mu _{\mathrm {Thu}}$
on
$\mu _{\mathrm {Thu}}$
on
![]() $\mathcal {ML}_g$
and its relation to Dehn–Thurston coordinates as described in Exercise 3.11. The following result of Masur is an analog of the fact that the Lebesgue measure is ergodic with respect to the action of
$\mathcal {ML}_g$
and its relation to Dehn–Thurston coordinates as described in Exercise 3.11. The following result of Masur is an analog of the fact that the Lebesgue measure is ergodic with respect to the action of
![]() $\mathrm {SL}(2,\mathbb {Z})$
on
$\mathrm {SL}(2,\mathbb {Z})$
on
![]() $\mathbb {R}^2$
. See Theorem 2.5.
$\mathbb {R}^2$
. See Theorem 2.5.
Theorem 5.3. [Reference MasurMas85]
The measure
![]() $\mu _{\mathrm {Thu}}$
is ergodic with respect to the action of
$\mu _{\mathrm {Thu}}$
is ergodic with respect to the action of
![]() $\mathrm {Mod}_g$
on
$\mathrm {Mod}_g$
on
![]() $\mathcal {ML}_g$
.
$\mathcal {ML}_g$
.
In analogy with the case of lattices, the ergodicity of the mapping class group action on
![]() $\mathcal {ML}_g$
can be used to study the weak-
$\mathcal {ML}_g$
can be used to study the weak-
![]() $\star $
limit points of the sequence of counting measures
$\star $
limit points of the sequence of counting measures
![]() $(\smash {\mu _L^\gamma })_{L>0}$
. The following crucial exercise is an analog of Proposition 2.8.
$(\smash {\mu _L^\gamma })_{L>0}$
. The following crucial exercise is an analog of Proposition 2.8.
Exercise 5.4. Let
![]() $\gamma := \sum _{i=1}^k a_i \gamma _i$
be an integral simple closed multi-curve on
$\gamma := \sum _{i=1}^k a_i \gamma _i$
be an integral simple closed multi-curve on
![]() $S_g$
. Show that every weak-
$S_g$
. Show that every weak-
![]() $\star $
limit point
$\star $
limit point
![]() $\mu ^\gamma $
of the sequence of counting measures
$\mu ^\gamma $
of the sequence of counting measures
![]() $(\smash {\mu _L^\gamma })_{L>0}$
introduced in equation (5.2) is of the form
$(\smash {\mu _L^\gamma })_{L>0}$
introduced in equation (5.2) is of the form
![]() $\mu ^\gamma = c \cdot \mu _{\mathrm {Thu}}$
for some constant
$\mu ^\gamma = c \cdot \mu _{\mathrm {Thu}}$
for some constant
![]() $c\geq 0$
. Hint: Follow the same approach as in the proof of Proposition 2.8 but working in Dehn–Thurston coordinates and recalling Exercise 3.11. More concretely, use a rough lattice points counting bound to show every limit point is absolutely continuous with respect to
$c\geq 0$
. Hint: Follow the same approach as in the proof of Proposition 2.8 but working in Dehn–Thurston coordinates and recalling Exercise 3.11. More concretely, use a rough lattice points counting bound to show every limit point is absolutely continuous with respect to
![]() $\mu _{\mathrm {Thu}}$
and then use Theorem 5.3 and Exercise 2.4 to conclude.
$\mu _{\mathrm {Thu}}$
and then use Theorem 5.3 and Exercise 2.4 to conclude.
5.5 Integration and integrability
Our next goal is to show that the constant
![]() $c \geq 0$
in the conclusion of Exercise 5.4 is positive and independent of the limit point
$c \geq 0$
in the conclusion of Exercise 5.4 is positive and independent of the limit point
![]() $\mu ^\gamma $
. Similar to the case of lattices, we achieve this goal by averaging over moduli space and using Mirzakhani’s integration formula.
$\mu ^\gamma $
. Similar to the case of lattices, we achieve this goal by averaging over moduli space and using Mirzakhani’s integration formula.
Recall that
![]() $\widehat {\mu }_{\mathrm {wp}}$
denotes the Weil–Petersson measure on
$\widehat {\mu }_{\mathrm {wp}}$
denotes the Weil–Petersson measure on
![]() $\mathcal {M}_g$
. Let
$\mathcal {M}_g$
. Let
![]() $\vec {\gamma } := (\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
$\vec {\gamma } := (\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $\mathbf {a} := \smash {(a_i)_{i=1}^k} \in \mathbb {R}_+^k$
be a vector of positive weights. On
$\mathbf {a} := \smash {(a_i)_{i=1}^k} \in \mathbb {R}_+^k$
be a vector of positive weights. On
![]() $S_g$
, consider the simple closed multi-curve given by
$S_g$
, consider the simple closed multi-curve given by
![]() $\mathbf {a} \cdot \vec {\gamma } := \smash {\sum _{i=1}^k a_i \gamma _i}$
. Recall the definition of the polynomial
$\mathbf {a} \cdot \vec {\gamma } := \smash {\sum _{i=1}^k a_i \gamma _i}$
. Recall the definition of the polynomial
![]() $V_g(\vec {\gamma },\mathbf {x})$
introduced in equation (4.3). Notice that
$V_g(\vec {\gamma },\mathbf {x})$
introduced in equation (4.3). Notice that
![]() $\mathrm {Stab}(\vec {\gamma }) \subseteq \mathrm {Mod}_g$
is a finite index subgroup of
$\mathrm {Stab}(\vec {\gamma }) \subseteq \mathrm {Mod}_g$
is a finite index subgroup of
![]() $\mathrm {Stab}(\mathbf {a} \cdot \vec {\gamma })$
. Define
$\mathrm {Stab}(\mathbf {a} \cdot \vec {\gamma })$
. Define
On
![]() $\smash {\mathbb {R}_+^k}$
, consider the standard coordinate system
$\smash {\mathbb {R}_+^k}$
, consider the standard coordinate system
![]() $\mathbf {x} := \smash {(x_i)_{i=1}^k}$
and the Lebesgue class measure
$\mathbf {x} := \smash {(x_i)_{i=1}^k}$
and the Lebesgue class measure
![]() $\mathbf {x} \cdot d\mathbf {x} := x_1 \cdots x_k \cdot dx_1 \cdots dx_k$
. The following exercise is an analog of Proposition 2.10 and Exercise 4.3.
$\mathbf {x} \cdot d\mathbf {x} := x_1 \cdots x_k \cdot dx_1 \cdots dx_k$
. The following exercise is an analog of Proposition 2.10 and Exercise 4.3.
Exercise 5.5. Let
![]() $\vec {\gamma } :=(\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
$\vec {\gamma } :=(\gamma _i)_{i=1}^k$
be an ordered simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $\mathbf {a}:= (a_i)_{i=1}^k \in \mathbb {R}_+^k$
be a vector of positive weights on the components of
$\mathbf {a}:= (a_i)_{i=1}^k \in \mathbb {R}_+^k$
be a vector of positive weights on the components of
![]() $\gamma $
. Using Exercise 4.7, show that, for every
$\gamma $
. Using Exercise 4.7, show that, for every
![]() $L> 0$
,
$L> 0$
,
 $$ \begin{align*} \int_{\mathcal{M}_g} s(X,\mathbf{a} \cdot \vec{\gamma},L) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = \int_{\mathbf{a} \cdot \mathbf{x} \leq L} V_g(\mathbf{a} \cdot \vec{\gamma},\mathbf{x}) \cdot \mathbf{x} \cdot d\mathbf{x}. \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_g} s(X,\mathbf{a} \cdot \vec{\gamma},L) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = \int_{\mathbf{a} \cdot \mathbf{x} \leq L} V_g(\mathbf{a} \cdot \vec{\gamma},\mathbf{x}) \cdot \mathbf{x} \cdot d\mathbf{x}. \end{align*} $$
Using this formula and Theorem 4.1, deduce that the function
 $$ \begin{align} P(\mathbf{a} \cdot \vec{\gamma},L) := \int_{\mathcal{M}_g} s(X,\mathbf{a} \cdot \vec{\gamma},L) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) \end{align} $$
$$ \begin{align} P(\mathbf{a} \cdot \vec{\gamma},L) := \int_{\mathcal{M}_g} s(X,\mathbf{a} \cdot \vec{\gamma},L) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) \end{align} $$
is a polynomial of degree
![]() $6g-6$
on L with rational leading coefficient.
$6g-6$
on L with rational leading coefficient.
Let
![]() $\gamma := \mathbf {a} \cdot \vec {\gamma } = \smash {\sum _{i=1}^k a_i \gamma _i}$
be a simple closed multi-curve on
$\gamma := \mathbf {a} \cdot \vec {\gamma } = \smash {\sum _{i=1}^k a_i \gamma _i}$
be a simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $P(\gamma ,L) = P(\mathbf {a} \cdot \vec {\gamma },L)$
be as in equation (5.4). Following Exercise 5.5, we define the frequency of
$P(\gamma ,L) = P(\mathbf {a} \cdot \vec {\gamma },L)$
be as in equation (5.4). Following Exercise 5.5, we define the frequency of
![]() $\gamma $
to be the positive rational number
$\gamma $
to be the positive rational number
Using Mirzakhani’s recursion for the Weil–Petersson volume polynomials
![]() $V_{g,b}(\mathbf {L})$
[Reference MirzakhaniMir07a, §5], the frequency of any simple closed curve can be computed explicitly by means of a recursive algorithm.
$V_{g,b}(\mathbf {L})$
[Reference MirzakhaniMir07a, §5], the frequency of any simple closed curve can be computed explicitly by means of a recursive algorithm.
Exercise 5.6. Let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
be non-separating and separating simple closed curves on
$\gamma _2$
be non-separating and separating simple closed curves on
![]() $S_2$
, respectively. Using Exercise 4.10, show that the frequencies of these simple closed curves are given by
$S_2$
, respectively. Using Exercise 4.10, show that the frequencies of these simple closed curves are given by
We now discuss an analog of the integrability bound in Exercise 2.11 for the function
![]() $s(X,\gamma ,L)$
. Let us first introduce a more precise statement of the collar lemma discussed in §3. A proof of this result can be found in [Reference Farb and MargalitFM12, Lemma 13.6]. Consider the width function
$s(X,\gamma ,L)$
. Let us first introduce a more precise statement of the collar lemma discussed in §3. A proof of this result can be found in [Reference Farb and MargalitFM12, Lemma 13.6]. Consider the width function
![]() $w \colon \mathbb {R}_+ \to \mathbb {R}_+$
given by
$w \colon \mathbb {R}_+ \to \mathbb {R}_+$
given by
 $$ \begin{align*} w(x) := \mathrm{arcsinh}\bigg( \frac{1}{\sinh ( x/ 2 )}\bigg). \end{align*} $$
$$ \begin{align*} w(x) := \mathrm{arcsinh}\bigg( \frac{1}{\sinh ( x/ 2 )}\bigg). \end{align*} $$
Lemma 5.7. Let
![]() $\alpha $
be a simple closed geodesic on a closed, orientable hyperbolic surface X. Denote by d the metric on X. Then, the subset
$\alpha $
be a simple closed geodesic on a closed, orientable hyperbolic surface X. Denote by d the metric on X. Then, the subset
![]() $N_{\alpha } \subseteq X$
defined as follows is an embedded annulus in X:
$N_{\alpha } \subseteq X$
defined as follows is an embedded annulus in X:
Let
![]() $\mathcal {P} := \smash {(\gamma _i)_{i=1}^{3g-3}}$
be a pair of pants decomposition of
$\mathcal {P} := \smash {(\gamma _i)_{i=1}^{3g-3}}$
be a pair of pants decomposition of
![]() $S_g$
and
$S_g$
and
![]() $\smash {(m_i,t_i)_{i=1}^{3g-3}}$
be a set of Dehn–Thurston coordinates of
$\smash {(m_i,t_i)_{i=1}^{3g-3}}$
be a set of Dehn–Thurston coordinates of
![]() $\mathcal {ML}_g$
induced by
$\mathcal {ML}_g$
induced by
![]() $\mathcal {P}$
. Given a measured geodesic lamination
$\mathcal {P}$
. Given a measured geodesic lamination
![]() $\unicode{x3bb} \in \mathcal {ML}_g$
and
$\unicode{x3bb} \in \mathcal {ML}_g$
and
![]() $X \in \mathcal {T}_g$
, define the combinatorial length of
$X \in \mathcal {T}_g$
, define the combinatorial length of
![]() $\unicode{x3bb} $
with respect to X and
$\unicode{x3bb} $
with respect to X and
![]() $\mathcal {P}$
as
$\mathcal {P}$
as
 $$ \begin{align*} L_\unicode{x3bb}(X,\mathcal{P}) := \sum_{i=1}^N (m_i(\gamma) \cdot w(\ell_{\gamma_i}(X)) + |t_i(\gamma)| \cdot \ell_{\gamma_i}(X)). \end{align*} $$
$$ \begin{align*} L_\unicode{x3bb}(X,\mathcal{P}) := \sum_{i=1}^N (m_i(\gamma) \cdot w(\ell_{\gamma_i}(X)) + |t_i(\gamma)| \cdot \ell_{\gamma_i}(X)). \end{align*} $$
For a simple closed curve
![]() $\alpha $
on
$\alpha $
on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {T}_g$
, this definition has a concrete interpretation: add the width
$X \in \mathcal {T}_g$
, this definition has a concrete interpretation: add the width
![]() $w(\ell _{\gamma _i}(X))$
of the collar given by Lemma 5.7 every time
$w(\ell _{\gamma _i}(X))$
of the collar given by Lemma 5.7 every time
![]() $\alpha $
intersects
$\alpha $
intersects
![]() $\gamma _i$
and add the length
$\gamma _i$
and add the length
![]() $\ell _{\gamma _i}(X)$
every time
$\ell _{\gamma _i}(X)$
every time
![]() $\alpha $
twists around
$\alpha $
twists around
![]() $\gamma _i$
. A pair of pants decomposition
$\gamma _i$
. A pair of pants decomposition
![]() $\mathcal {P} := \smash {(\gamma _i)_{i=1}^{3g-3}}$
of
$\mathcal {P} := \smash {(\gamma _i)_{i=1}^{3g-3}}$
of
![]() $S_g$
is said to be L-bounded with respect to
$S_g$
is said to be L-bounded with respect to
![]() $X \in \mathcal {T}_g$
for some
$X \in \mathcal {T}_g$
for some
![]() $L> 0$
if
$L> 0$
if
![]() $\ell _{\gamma _i}(X) \leq L$
for every
$\ell _{\gamma _i}(X) \leq L$
for every
![]() $i \in \{1,\ldots ,3g-3\}$
. The following result of Mirzakhani shows that combinatorial lengths approximate hyperbolic lengths.
$i \in \{1,\ldots ,3g-3\}$
. The following result of Mirzakhani shows that combinatorial lengths approximate hyperbolic lengths.
Proposition 5.8. [Reference MirzakhaniMir08b, Proposition 3.5]
For every
![]() $L\hspace{-1pt} >\hspace{-1pt} 0$
, there exists
$L\hspace{-1pt} >\hspace{-1pt} 0$
, there exists
![]() $C\hspace{-1pt} =\hspace{-1pt} C(L)\hspace{-1pt}>\hspace{-1pt} 0$
such that for every
$C\hspace{-1pt} =\hspace{-1pt} C(L)\hspace{-1pt}>\hspace{-1pt} 0$
such that for every
![]() $X \in \mathcal {T}_{g}$
and every pair of pants decomposition
$X \in \mathcal {T}_{g}$
and every pair of pants decomposition
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $S_{g}$
that is L-bounded with respect to X, there exist Dehn–Thurston coordinates
$S_{g}$
that is L-bounded with respect to X, there exist Dehn–Thurston coordinates
![]() $\smash {(m_i,t_i)_{i=1}^{3g-3}}$
of
$\smash {(m_i,t_i)_{i=1}^{3g-3}}$
of
![]() $\mathcal {ML}_{g}$
induced by
$\mathcal {ML}_{g}$
induced by
![]() $\mathcal {P}$
such that for every
$\mathcal {P}$
such that for every
![]() $\unicode{x3bb} \in \mathcal {ML}_{g}$
,
$\unicode{x3bb} \in \mathcal {ML}_{g}$
,
To prove the aforementioned integrability bound for the counting function
![]() $s(X,\gamma ,L)$
, we will also use the following stronger version of Bers’s theorem. For a proof, see [Reference Farb and MargalitFM12, Theorem 12.8].
$s(X,\gamma ,L)$
, we will also use the following stronger version of Bers’s theorem. For a proof, see [Reference Farb and MargalitFM12, Theorem 12.8].
Theorem 5.9. For every
![]() $\epsilon> 0$
, there exists
$\epsilon> 0$
, there exists
![]() $L = L(\epsilon )> 0$
with the following property. Let
$L = L(\epsilon )> 0$
with the following property. Let
![]() $X \in \mathcal {T}_{g}$
be a marked hyperbolic structure and
$X \in \mathcal {T}_{g}$
be a marked hyperbolic structure and
![]() $\gamma := (\gamma _i)_{i=1}^k$
be a simple closed multi-curve on
$\gamma := (\gamma _i)_{i=1}^k$
be a simple closed multi-curve on
![]() $S_g$
such that
$S_g$
such that
Then, there exists a completion of
![]() $\gamma $
to a pair of pants decomposition
$\gamma $
to a pair of pants decomposition
![]() $\mathcal {P}:= (\gamma _i)_{i=1}^{3g-3}$
of
$\mathcal {P}:= (\gamma _i)_{i=1}^{3g-3}$
of
![]() $S_g$
such that
$S_g$
such that
By Lemma 5.7, there exists a constant
![]() $\epsilon> 0$
such that on any closed, orientable hyperbolic surface, no two closed geodesics of length
$\epsilon> 0$
such that on any closed, orientable hyperbolic surface, no two closed geodesics of length
![]() $< \epsilon $
intersect. For the rest of this section, we fix such a constant and denote it by
$< \epsilon $
intersect. For the rest of this section, we fix such a constant and denote it by
![]() $\epsilon> 0$
. Consider the measurable function
$\epsilon> 0$
. Consider the measurable function
![]() $u \colon \mathcal {M}_g \to \mathbb {R}_+$
given for every
$u \colon \mathcal {M}_g \to \mathbb {R}_+$
given for every
![]() $X \in \mathcal {M}_g$
by
$X \in \mathcal {M}_g$
by
 $$ \begin{align*} u(X) := \prod_{\alpha \colon \ell_{\gamma}(X) < \epsilon} \frac{1}{\ell_{\alpha}(X)}, \end{align*} $$
$$ \begin{align*} u(X) := \prod_{\alpha \colon \ell_{\gamma}(X) < \epsilon} \frac{1}{\ell_{\alpha}(X)}, \end{align*} $$
where the product runs over all simple closed geodesics
![]() $\alpha $
on X of length
$\alpha $
on X of length
![]() $\ell _{\alpha }(X) < \epsilon $
. We interpret empty products as taking the value
$\ell _{\alpha }(X) < \epsilon $
. We interpret empty products as taking the value
![]() $1$
. The following exercise is an analog of Exercise 2.11.
$1$
. The following exercise is an analog of Exercise 2.11.
Exercise 5.10. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
. Show there exists a constant
$S_g$
. Show there exists a constant
![]() $C> 0$
such that for every
$C> 0$
such that for every
![]() $X \in \mathcal {M}_g$
and every
$X \in \mathcal {M}_g$
and every
![]() $L> 0$
,
$L> 0$
,
Additionally, show that the function
![]() $u \colon \mathcal {M}_g \to \mathbb {R}_+$
is integrable with respect to
$u \colon \mathcal {M}_g \to \mathbb {R}_+$
is integrable with respect to
![]() $\widehat {\mu }_{\mathrm {wp}}$
, that is,
$\widehat {\mu }_{\mathrm {wp}}$
, that is,
 $$ \begin{align} \int_{\mathcal{M}_g} u(X) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) < \infty. \end{align} $$
$$ \begin{align} \int_{\mathcal{M}_g} u(X) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) < \infty. \end{align} $$
Hint: To prove equation (5.6), use Proposition 5.8 and Theorem 5.9 to reduce to a lattice point counting problem in Dehn–Thurston coordinates. To prove equation (5.7), follow the same approach as in Exercise 3.8.
For every marked hyperbolic structure
![]() $X \in \mathcal {T}_g$
, denote
$X \in \mathcal {T}_g$
, denote
As the Thurston measure
![]() $\mu _{\mathrm {Thu}}$
is invariant with respect to the
$\mu _{\mathrm {Thu}}$
is invariant with respect to the
![]() $\mathrm {Mod}_g$
action on
$\mathrm {Mod}_g$
action on
![]() $\mathcal {ML}_g$
, the value
$\mathcal {ML}_g$
, the value
![]() $B(X)$
is independent of the marking of
$B(X)$
is independent of the marking of
![]() $X \in \mathcal {T}_g$
and depends only on the underlying hyperbolic structure
$X \in \mathcal {T}_g$
and depends only on the underlying hyperbolic structure
![]() $X \in \mathcal {M}_g$
. Thus, equation (5.8) gives rise to a function
$X \in \mathcal {M}_g$
. Thus, equation (5.8) gives rise to a function
![]() $B \colon \mathcal {M}_g \to \mathbb {R}_+$
known as the Mirzakahani function.
$B \colon \mathcal {M}_g \to \mathbb {R}_+$
known as the Mirzakahani function.
Exercise 5.11. Show there exists a constant
![]() $C> 0$
such that for every
$C> 0$
such that for every
![]() $X \in \mathcal {M}_g$
,
$X \in \mathcal {M}_g$
,
Conclude that the function
![]() $B \colon \mathcal {M}_g \to \mathbb {R}_+$
is integrable with respect to
$B \colon \mathcal {M}_g \to \mathbb {R}_+$
is integrable with respect to
![]() $\widehat {\mu }_{\mathrm {wp}}$
, that is,
$\widehat {\mu }_{\mathrm {wp}}$
, that is,
 $$ \begin{align} \int_{\mathcal{M}_g} B(X) \thinspace d \widehat{\mu}_{\mathrm{wp}}(X) < \infty. \end{align} $$
$$ \begin{align} \int_{\mathcal{M}_g} B(X) \thinspace d \widehat{\mu}_{\mathrm{wp}}(X) < \infty. \end{align} $$
Hint: To prove equation (5.9), use Proposition 5.8, Theorem 5.9, and interpret
![]() $\mu _{\mathrm {Thu}}$
as Lebesgue measure in Dehn–Thurston coordinates using Exercise 3.11. To prove equation (5.10), use Exercise 5.10.
$\mu _{\mathrm {Thu}}$
as Lebesgue measure in Dehn–Thurston coordinates using Exercise 3.11. To prove equation (5.10), use Exercise 5.10.
Following Exercise 5.11, we consider the constant
![]() $b_g> 0$
defined as
$b_g> 0$
defined as
 $$ \begin{align} b_g := \int_{\mathcal{M}_g} B(X) \thinspace d \widehat{\mu}_{\mathrm{wp}}(X). \end{align} $$
$$ \begin{align} b_g := \int_{\mathcal{M}_g} B(X) \thinspace d \widehat{\mu}_{\mathrm{wp}}(X). \end{align} $$
5.6 Equidistribution of counting measures
We are finally ready to prove that the sequence of counting measure
![]() $\smash {(\mu ^\gamma _L)_{L> 0}}$
on
$\smash {(\mu ^\gamma _L)_{L> 0}}$
on
![]() $\mathcal {ML}_g$
converges in the weak-
$\mathcal {ML}_g$
converges in the weak-
![]() $\star $
topology to a constant multiple of the Thurston measure
$\star $
topology to a constant multiple of the Thurston measure
![]() $\mu _{\mathrm {Thu}}$
. The following exercise is an analog of Theorem 2.14.
$\mu _{\mathrm {Thu}}$
. The following exercise is an analog of Theorem 2.14.
Exercise 5.12. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
. The goal of this exercise is to show that, with respect to the weak-
$S_g$
. The goal of this exercise is to show that, with respect to the weak-
![]() $\star $
topology for measures on
$\star $
topology for measures on
![]() $\mathcal {ML}_g$
,
$\mathcal {ML}_g$
,
 $$ \begin{align*} \lim_{L \to \infty} \mu_L^\gamma = \frac{c(\gamma)}{b_g} \cdot \mu_{\mathrm{Thu}}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \mu_L^\gamma = \frac{c(\gamma)}{b_g} \cdot \mu_{\mathrm{Thu}}. \end{align*} $$
Suppose
![]() $(L_k)_{k \in \mathbb{N}}$
is a sequence in
$(L_k)_{k \in \mathbb{N}}$
is a sequence in
![]() $\mathbb {R}_+$
with
$\mathbb {R}_+$
with
![]() $L_k \nearrow +\infty $
as
$L_k \nearrow +\infty $
as
![]() $k \to \infty $
and such that, for some
$k \to \infty $
and such that, for some
![]() $c \geq 0$
,
$c \geq 0$
,
We compute the following limit in two different ways,
 $$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_g} \frac{s(X,\gamma,L_k)}{L_k^{6g-6}} \thinspace d\widehat{\mu}_{\mathrm{wp}}(X). \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_g} \frac{s(X,\gamma,L_k)}{L_k^{6g-6}} \thinspace d\widehat{\mu}_{\mathrm{wp}}(X). \end{align*} $$
-
(1) Use Exercise 5.5 to show that
 $$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_g} \frac{s(X,\gamma,L_k)}{L_k^{6g-6}} \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = c(\gamma). \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_g} \frac{s(X,\gamma,L_k)}{L_k^{6g-6}} \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = c(\gamma). \end{align*} $$
-
(2) Use Exercise 5.10 and the dominate convergence theorem to show that
 $$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_g} \frac{s(X,\gamma,L_k)}{L_k^{6g-6}} \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = c \cdot b_g. \end{align*} $$
$$ \begin{align*} \lim_{k \to \infty} \int_{\mathcal{M}_g} \frac{s(X,\gamma,L_k)}{L_k^{6g-6}} \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) = c \cdot b_g. \end{align*} $$
-
(3) Use the previous parts and Exercise 5.4 to conclude that
 $$ \begin{align*} \lim_{L \to \infty} \mu_L^\gamma = \frac{c(\gamma)}{b_g} \cdot \mu_{\mathrm{Thu}}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \mu_L^\gamma = \frac{c(\gamma)}{b_g} \cdot \mu_{\mathrm{Thu}}. \end{align*} $$
5.7 Counting simple closed multi-curves
We have developed all the tools needed to prove the following more precise version of Theorem 5.2.
Exercise 5.13. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $X \in \mathcal {T}_g$
be a marked hyperbolic structure on
$X \in \mathcal {T}_g$
be a marked hyperbolic structure on
![]() $S_g$
. Show that the following identity holds:
$S_g$
. Show that the following identity holds:
 $$ \begin{align*} \lim_{L \to \infty} \frac{s(X,\gamma,L)}{L^{6g-6}} = \frac{c(\gamma) \cdot B(X)}{b_g}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \frac{s(X,\gamma,L)}{L^{6g-6}} = \frac{c(\gamma) \cdot B(X)}{b_g}. \end{align*} $$
Hint: Follow the same approach as in the proof of Theorem 2.16. Aside from Exercise 5.12, it will be useful to recall the identity in equation (5.3) as well as Exercise 3.12.
Now, we direct our attention to Theorem 1.1, the main result of this survey.
Exercise 5.14. Using equation (5.1) and Exercise 5.13, prove Theorem 1.1, that is, show that for every closed, orientable hyperbolic surface X of genus
![]() $g \geq 2$
, there exists a constant
$g \geq 2$
, there exists a constant
![]() $n(X)> 0$
such that
$n(X)> 0$
such that
Let us end this section by following a more precise version of Theorem 1.2.
Exercise 5.15. Let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
be non-separating and separating simple closed curves on
$\gamma _2$
be non-separating and separating simple closed curves on
![]() $S_2$
, respectively. Using Exercises 5.6 and 5.13, show that on any genus
$S_2$
, respectively. Using Exercises 5.6 and 5.13, show that on any genus
![]() $2$
hyperbolic surface
$2$
hyperbolic surface
![]() $X \in \mathcal {M}_2$
, it is
$X \in \mathcal {M}_2$
, it is
![]() $48$
times more likely for a long random simple closed geodesic to be non-separating rather than separating, that is, show that
$48$
times more likely for a long random simple closed geodesic to be non-separating rather than separating, that is, show that
6 Beyond simple closed geodesics
6.1 Outline of this section
In this section, we give a brief overview of several counting results for closed curves on surfaces and other related objects that have been proved since the debut of Mirzakhani’s thesis. Rather than exhaustively covering the great amount of material available, we aim at giving a landscape picture of the relevance of these results and of the variety of techniques behind their proofs. In particular, although many of the results that follow hold for surfaces with punctures, we focus on the case of closed surfaces. The reader is encouraged to look into the cited references for more details.
6.2 General length functions
For the rest of this section, we fix an integer
![]() $g \geq 2$
and a connected, oriented, closed surface
$g \geq 2$
and a connected, oriented, closed surface
![]() $S_g$
of genus g. Let
$S_g$
of genus g. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be a simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be a simple closed multi-curve on
![]() $S_g$
. Consider a continuous function
$S_g$
. Consider a continuous function
![]() $\ell \colon \mathcal {ML}_g \to \mathbb {R}_+$
on the space of measured geodesic laminations that is homogeneous, that is, such that
$\ell \colon \mathcal {ML}_g \to \mathbb {R}_+$
on the space of measured geodesic laminations that is homogeneous, that is, such that
![]() $\ell (t \cdot \unicode{x3bb} ) = t \cdot \ell (\unicode{x3bb} )$
for every
$\ell (t \cdot \unicode{x3bb} ) = t \cdot \ell (\unicode{x3bb} )$
for every
![]() $t>0$
and every
$t>0$
and every
![]() $\unicode{x3bb} \in \mathcal {ML}_g$
. Interesting examples of such functions include the square root of extremal length with respect to a given conformal structure [Reference KerckhoffKer80] and the length of geodesic representatives with respect to an arbitrary negatively curved metric [Reference OtalOta90]. For every
$\unicode{x3bb} \in \mathcal {ML}_g$
. Interesting examples of such functions include the square root of extremal length with respect to a given conformal structure [Reference KerckhoffKer80] and the length of geodesic representatives with respect to an arbitrary negatively curved metric [Reference OtalOta90]. For every
![]() $L> 0$
, consider the counting function
$L> 0$
, consider the counting function
Furthermore, consider the finite, positive constant
Recall the definition of the constants
![]() $c(\gamma )> 0$
and
$c(\gamma )> 0$
and
![]() $b_g> 0$
introduced in equations (5.5) and (5.11). A careful consideration of the techniques introduced in the proof of Theorem 5.2 shows that similar asymptotic estimates can be proved in this more general setting. Indeed, the following holds.
$b_g> 0$
introduced in equations (5.5) and (5.11). A careful consideration of the techniques introduced in the proof of Theorem 5.2 shows that similar asymptotic estimates can be proved in this more general setting. Indeed, the following holds.
Exercise 6.1. Let
![]() $\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
$\gamma := \smash {\sum _{i=1}^k a_i \gamma _i}$
be an integral simple closed multi-curve on
![]() $S_g$
and
$S_g$
and
![]() $\ell \colon \mathcal {ML}_g \to \mathbb {R}_+$
be a continuous, homogeneous function. Show that the following identity holds:
$\ell \colon \mathcal {ML}_g \to \mathbb {R}_+$
be a continuous, homogeneous function. Show that the following identity holds:
 $$ \begin{align*} \lim_{L \to \infty} \frac{s(\ell,\gamma,L)}{L^{6g-6}} = \frac{c(\gamma) \cdot B(\ell)}{b_g}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \frac{s(\ell,\gamma,L)}{L^{6g-6}} = \frac{c(\gamma) \cdot B(\ell)}{b_g}. \end{align*} $$
Hint: Follow the same approach as in Exercise 5.13.
6.3 Non-simple closed geodesics
One can also consider counting problems for closed geodesics that are not simple. Extending the definition for simple closed curves, we say two closed curves on homeomorphic surfaces have the same topological type if there exists a homeomorphism between the surfaces that identifies the free homotopy classes of the curves. A closed curve is said to be filling if every homotopically non-trivial closed curve on the surface intersects the curve.
Let
![]() $X \in \mathcal {T}_g$
be a marked hyperbolic structure and
$X \in \mathcal {T}_g$
be a marked hyperbolic structure and
![]() $\gamma $
be a filling closed curve on
$\gamma $
be a filling closed curve on
![]() $S_g$
. For every
$S_g$
. For every
![]() $L> 0$
, consider the counting function
$L> 0$
, consider the counting function
This quantity does not depend on the marking of
![]() $X \in \mathcal {T}_g$
and corresponds to the number of closed geodesics on X of the same topological type as
$X \in \mathcal {T}_g$
and corresponds to the number of closed geodesics on X of the same topological type as
![]() $\gamma $
and length
$\gamma $
and length
![]() $\leq L$
. Consider the finite constant
$\leq L$
. Consider the finite constant
where
![]() $i(\gamma ,\unicode{x3bb} )$
denotes the geometric intersection number between
$i(\gamma ,\unicode{x3bb} )$
denotes the geometric intersection number between
![]() $\gamma $
and
$\gamma $
and
![]() $\unicode{x3bb} $
, for a precise definition, see for instance [Reference BonahonBon88], and
$\unicode{x3bb} $
, for a precise definition, see for instance [Reference BonahonBon88], and
![]() $\mathrm {Stab}(\gamma ) \subseteq \mathrm {Mod}_g$
denotes the stabilizer of
$\mathrm {Stab}(\gamma ) \subseteq \mathrm {Mod}_g$
denotes the stabilizer of
![]() $\gamma $
with respect to the natural mapping class group action. Recall the definition of the Mirzakhani function
$\gamma $
with respect to the natural mapping class group action. Recall the definition of the Mirzakhani function
![]() $B \colon \mathcal {M}_g \to \mathbb {R}_+$
in equation (5.8). In [Reference MirzakhaniMir16], Mirzakhani introduced novel techniques to prove the following result.
$B \colon \mathcal {M}_g \to \mathbb {R}_+$
in equation (5.8). In [Reference MirzakhaniMir16], Mirzakhani introduced novel techniques to prove the following result.
Theorem 6.2. [Reference MirzakhaniMir16, Theorem 1.1]
Let
![]() $X \in \mathcal {M}_g$
be a hyperbolic structure and
$X \in \mathcal {M}_g$
be a hyperbolic structure and
![]() $\gamma $
be a filling closed curve on
$\gamma $
be a filling closed curve on
![]() $S_g$
. Then, the following asymptotic formula holds:
$S_g$
. Then, the following asymptotic formula holds:
 $$ \begin{align*} \lim_{L \to \infty} \frac{f(X,\gamma,L)}{L^{6g-6}} = \frac{c(\gamma) \cdot B(X)}{b_g}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \frac{f(X,\gamma,L)}{L^{6g-6}} = \frac{c(\gamma) \cdot B(X)}{b_g}. \end{align*} $$
Mirzakhani’s proof of Theorem 6.2 is inspired by work of Margulis [Reference MargulisMar70] and relies on previous work by herself on the ergodic theory of the earthquake flow [Reference MirzakhaniMir08a]. More concretely, instead of counting the points in a mapping class group orbit of a filling closed curve, one can count the points in a mapping class group orbit of Teichmüller space. Then, the length of a filling closed curve on Teichmüller space is asymptotically a piecewise linear function with respect to Fenchel–Nielsen coordinates. Partitioning Teichmüller space into finer and finer cones with respect to these coordinates, one can study the equidistribution of these cones as the length of the filling closed curve goes to infinity. This can be done by using the earthquake flow, a generalization of Fenchel–Nielsen twists along simple closed geodesics but for measured geodesic laminations, and by following the general approach introduced by Margulis in his thesis.
A result analogous to Theorem 6.2 for closed geodesics of any topological type was later proved by Erlandsson and Souto [Reference Erlandsson and SoutoES19] using original arguments introduced in their earlier work [Reference Erlandsson and SoutoES16]. The main idea of their approach is to consider counting measures as in equation (5.2), but defined for general closed curves that are not necessarily simple. Technically speaking, such measures are defined on the space of geodesic currents, an analog of the space of measured geodesic laminations, but for closed geodesics with self-intersections; this space will be introduce below. Similar to Mirzakhani’s original approach in [Reference MirzakhaniMir08b], the proof then boils down to showing that such counting measures converge in the weak-
![]() $\star $
topology to the Thurston measure. The main idea to achieve this is to study the procedure of smoothing a non-simple closed geodesic at its self-intersections.
$\star $
topology to the Thurston measure. The main idea to achieve this is to study the procedure of smoothing a non-simple closed geodesic at its self-intersections.
6.4 Geodesic currents
In [Reference BonahonBon88], Bonahon gave a unified treatment of several seemingly unrelated notions of length for closed curves on closed, orientable surfaces using the concept of geodesic currents.
To define geodesic currents, let us endow the surface
![]() $S_g$
with an auxiliary hyperbolic metric. The projective tangent bundle
$S_g$
with an auxiliary hyperbolic metric. The projective tangent bundle
![]() $PTS_g$
admits a one-dimensional foliation by lifts of geodesics on
$PTS_g$
admits a one-dimensional foliation by lifts of geodesics on
![]() $S_g$
. A geodesic current on
$S_g$
. A geodesic current on
![]() $S_g$
is a Radon transverse measure of the geodesic foliation of
$S_g$
is a Radon transverse measure of the geodesic foliation of
![]() $PTS_g$
. Equivalently, a geodesic current on
$PTS_g$
. Equivalently, a geodesic current on
![]() $S_g$
is a
$S_g$
is a
![]() $\pi _1(S_g)$
-invariant Radon measure on the space of unoriented geodesics of the universal cover of
$\pi _1(S_g)$
-invariant Radon measure on the space of unoriented geodesics of the universal cover of
![]() $S_g$
. Endow the space of geodesic currents on
$S_g$
. Endow the space of geodesic currents on
![]() $S_g$
with the weak-
$S_g$
with the weak-
![]() $\star $
topology. Different choices of auxiliary hyperbolic metrics on
$\star $
topology. Different choices of auxiliary hyperbolic metrics on
![]() $S_g$
yield canonically identified spaces of geodesic currents [Reference BonahonBon88, Fact 1]. Denote the space of geodesic currents on
$S_g$
yield canonically identified spaces of geodesic currents [Reference BonahonBon88, Fact 1]. Denote the space of geodesic currents on
![]() $S_g$
by
$S_g$
by
![]() $\mathcal {C}_g$
. This space supports a natural
$\mathcal {C}_g$
. This space supports a natural
![]() $\mathbb {R}_+$
scaling action and a natural
$\mathbb {R}_+$
scaling action and a natural
![]() $\mathrm {Mod}_g$
action [Reference Rafi and SoutoRS19, §2].
$\mathrm {Mod}_g$
action [Reference Rafi and SoutoRS19, §2].
Free homotopy classes of weighted, unoriented closed curves on
![]() $S_g$
embed into
$S_g$
embed into
![]() $\mathcal {C}_g$
by considering their geodesic representatives with respect to any auxiliary hyperbolic metric. By the work of Bonahon [Reference BonahonBon88, Proposition 2], this embedding is dense. Moreover, the geometric intersection number pairing for closed curves on
$\mathcal {C}_g$
by considering their geodesic representatives with respect to any auxiliary hyperbolic metric. By the work of Bonahon [Reference BonahonBon88, Proposition 2], this embedding is dense. Moreover, the geometric intersection number pairing for closed curves on
![]() $S_g$
extends in a unique way to a continuous, symmetric, bilinear pairing
$S_g$
extends in a unique way to a continuous, symmetric, bilinear pairing
![]() $i(\cdot ,\cdot )$
on
$i(\cdot ,\cdot )$
on
![]() $\mathcal {C}_g$
[Reference BonahonBon88, Proposition 3]. In this sense, geodesic currents are to closed curves what measured geodesic laminations are to simple closed curves.
$\mathcal {C}_g$
[Reference BonahonBon88, Proposition 3]. In this sense, geodesic currents are to closed curves what measured geodesic laminations are to simple closed curves.
Many different spaces of metrics on
![]() $S_g$
embed into
$S_g$
embed into
![]() $\mathcal {C}_g$
in such a way that the geometric intersection number of a metric with any closed curve is equal to the length of the geodesic representatives of the closed curve with respect to the metric. The geodesic current corresponding to any such metric is usually referred to as its Liouville current. Examples of metrics admitting Liouville currents include hyperbolic metrics [Reference BonahonBon88] and negatively curved Riemannian metrics [Reference OtalOta90].
$\mathcal {C}_g$
in such a way that the geometric intersection number of a metric with any closed curve is equal to the length of the geodesic representatives of the closed curve with respect to the metric. The geodesic current corresponding to any such metric is usually referred to as its Liouville current. Examples of metrics admitting Liouville currents include hyperbolic metrics [Reference BonahonBon88] and negatively curved Riemannian metrics [Reference OtalOta90].
A geodesic current
![]() $\alpha \in \mathcal {C}_g$
is said to be filling if
$\alpha \in \mathcal {C}_g$
is said to be filling if
![]() $i(\alpha ,\beta )> 0$
for every non-zero
$i(\alpha ,\beta )> 0$
for every non-zero
![]() $\beta \in \mathcal {C}_g$
. Relevant examples of filling geodesic currents include free homotopy classes of unoriented filling closed curves and the Liouville currents introduced above. Filling geodesic currents
$\beta \in \mathcal {C}_g$
. Relevant examples of filling geodesic currents include free homotopy classes of unoriented filling closed curves and the Liouville currents introduced above. Filling geodesic currents
![]() $\alpha \in \mathcal {C}_g$
have finite stabilizers
$\alpha \in \mathcal {C}_g$
have finite stabilizers
![]() $\mathrm {Stab}(\alpha ) \subseteq \mathrm {Mod}_g$
with respect to the natural mapping class group action [Reference Erlandsson and MondelloEM22].
$\mathrm {Stab}(\alpha ) \subseteq \mathrm {Mod}_g$
with respect to the natural mapping class group action [Reference Erlandsson and MondelloEM22].
Consider a continuous function
![]() $\ell \colon \mathcal {C}_g \to \mathbb {R}_+$
that is homogeneous, that is, such that
$\ell \colon \mathcal {C}_g \to \mathbb {R}_+$
that is homogeneous, that is, such that
![]() $\ell (t~\cdot ~\alpha ) = t \cdot \ell (\alpha )$
for every
$\ell (t~\cdot ~\alpha ) = t \cdot \ell (\alpha )$
for every
![]() $t> 0$
and every
$t> 0$
and every
![]() $\alpha \in \mathcal {C}_g$
. Let
$\alpha \in \mathcal {C}_g$
. Let
![]() $\alpha \in \mathcal {C}_g$
be a filling geodesic current. For every
$\alpha \in \mathcal {C}_g$
be a filling geodesic current. For every
![]() $L> 0$
, define
$L> 0$
, define
Furthermore, consider the finite, positive constant
In [Reference Rafi and SoutoRS19], Rafi and Souto proved the following generalization of Theorem 6.2.
Theorem 6.3. [Reference Rafi and SoutoRS19, Main Theorem]
Let
![]() $\ell \colon \mathcal {C}_g \to \mathbb {R}_+$
be a continuous, homogeneous function and
$\ell \colon \mathcal {C}_g \to \mathbb {R}_+$
be a continuous, homogeneous function and
![]() $\alpha \in \mathcal {C}_g$
be a filling geodesic current. Then, the following asymptotic estimate holds:
$\alpha \in \mathcal {C}_g$
be a filling geodesic current. Then, the following asymptotic estimate holds:
 $$ \begin{align*} \lim_{L \to \infty} \frac{\mathrm{cur}(\ell,\alpha,L)}{L^{6g-6}} = \frac{B(\ell) \cdot c(\alpha)}{b_g}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \frac{\mathrm{cur}(\ell,\alpha,L)}{L^{6g-6}} = \frac{B(\ell) \cdot c(\alpha)}{b_g}. \end{align*} $$
Theorem 6.3 was later generalized by Erlandsson and Souto for non-filling geodesic currents [Reference Erlandsson and SoutoES22]. The proof of Theorem 6.3 follows a similar approach to the arguments of Erlandsson and Souto described above, but involves other technical hurdles. The real power of this result comes from its applications. As a remarkable application of Theorem 6.3, Rafi and Souto proved an asymptotic formula for the number of points in a mapping class group orbit of Teichmüller space that lie within a ball of given center and large radius with respect to Thurston’s asymmetric metric; Thurston’s asymmetric metric quantifies the minimal Lipschitz constant among Lipschitz maps between marked hyperbolic surfaces [Reference ThurstonThu98]. Counting problems of this nature have been extensively studied in homogeneous dynamics and, in the setting of Teichmüller space, were previously studied by Athreya et al [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12]; later, we describe this work in more detail.
6.5 Square-tiled surfaces
A square-tiled surface is a closed, connected, oriented surface constructed from finitely many disjoint unit area squares on the complex plane, with sides parallel to the real and imaginary axes, by identifying pairs of sides by translation and/or ![]() rotation. Any such surface inherits a singular flat metric from the complex plane; the singularities of the metric are cone points with total angle an integer multiple of
rotation. Any such surface inherits a singular flat metric from the complex plane; the singularities of the metric are cone points with total angle an integer multiple of
![]() $\pi $
. For simplicity, we only consider square-tiled surfaces with no cone points of total angle
$\pi $
. For simplicity, we only consider square-tiled surfaces with no cone points of total angle
![]() $\pi $
. The horizontal core multi-curve of a square tiled-surface is the integrally weighted simple closed multi-curve obtained by concatenating the horizontal segments running through the middle of each square. The vertical core multi-curve of a square-tiled surface is defined in an analogous way. See Figure 17 for an example.
$\pi $
. The horizontal core multi-curve of a square tiled-surface is the integrally weighted simple closed multi-curve obtained by concatenating the horizontal segments running through the middle of each square. The vertical core multi-curve of a square-tiled surface is defined in an analogous way. See Figure 17 for an example.

Figure 17 Example of a square-tiled surface of genus
![]() $2$
. The horizontal core multi-curve is
$2$
. The horizontal core multi-curve is
![]() $\alpha _1 + 2 \alpha _2$
. The vertical core multi-curve is
$\alpha _1 + 2 \alpha _2$
. The vertical core multi-curve is
![]() $\beta _1 + \beta _2 + \beta _3$
(colour online).
$\beta _1 + \beta _2 + \beta _3$
(colour online).
Recall that two integrally weighted simple closed multi-curves on homeomorphic surfaces have the same topological type if there exists a homeomorphism between the surfaces mapping one multi-curve to the other preserving the weights. Let
![]() $\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
be an integral simple closed multi-curve on
$\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
be an integral simple closed multi-curve on
![]() $S_g$
. For every
$S_g$
. For every
![]() $L> 0$
, consider the counting function
$L> 0$
, consider the counting function
 $$ \begin{align*} sq(\alpha,L) := \# \left\lbrace \begin{array}{@{}c@{}} \text{square-tiled surfaces with horizontal core multi-curve}\\ \text{of the same topological type as } \alpha \text{ and} \leq L \text{ squares} \end{array} \right\rbrace /\sim, \end{align*} $$
$$ \begin{align*} sq(\alpha,L) := \# \left\lbrace \begin{array}{@{}c@{}} \text{square-tiled surfaces with horizontal core multi-curve}\\ \text{of the same topological type as } \alpha \text{ and} \leq L \text{ squares} \end{array} \right\rbrace /\sim, \end{align*} $$
where
![]() $\sim $
denotes the equivalence relation induced by cut and paste operations. As in the counting problems above, we are interested in the asymptotics of
$\sim $
denotes the equivalence relation induced by cut and paste operations. As in the counting problems above, we are interested in the asymptotics of
![]() $\mathrm {sq}(\alpha ,L)$
as
$\mathrm {sq}(\alpha ,L)$
as
![]() $L \to \infty $
. Denote by
$L \to \infty $
. Denote by
 $$ \begin{align} \epsilon_{g} := \begin{cases} 2 & \text{if } g=2, \\ 1 & \text{if } g \neq 2,\\ \end{cases} \end{align} $$
$$ \begin{align} \epsilon_{g} := \begin{cases} 2 & \text{if } g=2, \\ 1 & \text{if } g \neq 2,\\ \end{cases} \end{align} $$
the number of automorphisms of a generic square-tiled surface of genus g. Recall the definition of the constants
![]() $c(\gamma )> 0$
introduced in equation (5.5).
$c(\gamma )> 0$
introduced in equation (5.5).
Theorem 6.4. Let
![]() $\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
be an integral simple closed multi-curve on
$\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
be an integral simple closed multi-curve on
![]() $S_g$
. Then,
$S_g$
. Then,
One can also consider more refined counting functions of square-tiled surfaces. Let
![]() $\alpha := \smash {\sum _{i=1}^k \alpha _i \alpha _i}$
and
$\alpha := \smash {\sum _{i=1}^k \alpha _i \alpha _i}$
and
![]() $\beta := \smash {\sum _{j=1}^l b_j \beta _j}$
be integral simple closed multi-curves on
$\beta := \smash {\sum _{j=1}^l b_j \beta _j}$
be integral simple closed multi-curves on
![]() $S_g$
. For every
$S_g$
. For every
![]() $L> 0$
, denote
$L> 0$
, denote
 $$ \begin{align*} sq(\alpha,\beta,L) := \# \left\lbrace \begin{array}{@{}c@{}} \text{square-tiled surfaces with horizontal core multi-curve of }\\ \text{the same topological type as } \alpha \text{ and vertical core multi-curve}\\ \text{ of the same topological type as } \beta \text{ and} \leq L \text{ squares} \end{array} \right\rbrace /\sim, \end{align*} $$
$$ \begin{align*} sq(\alpha,\beta,L) := \# \left\lbrace \begin{array}{@{}c@{}} \text{square-tiled surfaces with horizontal core multi-curve of }\\ \text{the same topological type as } \alpha \text{ and vertical core multi-curve}\\ \text{ of the same topological type as } \beta \text{ and} \leq L \text{ squares} \end{array} \right\rbrace /\sim, \end{align*} $$
where
![]() $\sim $
denotes the equivalence relation induced by cut and paste operations.
$\sim $
denotes the equivalence relation induced by cut and paste operations.
Theorem 6.5. Let
![]() $\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
and
$\alpha := \smash {\sum _{i=1}^k a_i \alpha _i}$
and
![]() $\beta := \smash {\sum _{j=1}^l b_j \beta _j}$
be integral simple closed multi-curves on
$\beta := \smash {\sum _{j=1}^l b_j \beta _j}$
be integral simple closed multi-curves on
![]() $S_g$
. Then, the following asymptotic formula holds:
$S_g$
. Then, the following asymptotic formula holds:
Theorems 6.4 and 6.5 were originally proved by Delecroix et al using algebro-geometric methods [Reference Delecroix, Goujard, Zograf and ZorichDGZZ21]. Different proofs of these theorems were later provided in [Reference Arana-HerreraAra20]. These proofs made crucial use of the results of Mirzakhani discussed in this survey. Indeed, square-tiled surfaces are parameterized by filling pairs of integral simple closed multi-curves [Reference Hubbard and MasurHM79]. Through this parameterization, it is possible to recast Theorems 6.4 and 6.5 as counting problems for simple closed multi-curves, which one can then tackle using Mirzakhani’s original approach.
6.6 Individual components of multi-curves
Inspired by Mirzakhani’s counting theorems, Wolpert conjectured that analogous results should hold for countings of simple closed multi-geodesics that keep track of the hyperbolic length of individual components, rather than just the total hyperbolic length.
For instance, let
![]() $X \in \mathcal {M}_g$
be a closed, connected, oriented hyperbolic surface of genus
$X \in \mathcal {M}_g$
be a closed, connected, oriented hyperbolic surface of genus
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $\vec {\gamma } := (\gamma _1,\ldots ,\gamma _k)$
be an ordered simple closed multi-curve on
$\vec {\gamma } := (\gamma _1,\ldots ,\gamma _k)$
be an ordered simple closed multi-curve on
![]() $S_g$
with
$S_g$
with
![]() $1 \leq k \leq 3g-3$
components. For every
$1 \leq k \leq 3g-3$
components. For every
![]() $L> 0$
, consider the counting function
$L> 0$
, consider the counting function
 $$ \begin{align*} m(X,\vec{\gamma},L) := \# \left\lbrace \begin{array}{@{}c@{}} \text{ordered simple closed multi-geodesics } \vec{\alpha} :=(\alpha_1,\ldots,\alpha_k) \text{ on } X \\ \text{of the same topological type as } \vec{\gamma} \text{ with} \max_{i=1,\ldots,k} \ell_{\alpha_i}(X) \leq L \hspace{-0.1cm} \nonumber \end{array} \right\rbrace. \end{align*} $$
$$ \begin{align*} m(X,\vec{\gamma},L) := \# \left\lbrace \begin{array}{@{}c@{}} \text{ordered simple closed multi-geodesics } \vec{\alpha} :=(\alpha_1,\ldots,\alpha_k) \text{ on } X \\ \text{of the same topological type as } \vec{\gamma} \text{ with} \max_{i=1,\ldots,k} \ell_{\alpha_i}(X) \leq L \hspace{-0.1cm} \nonumber \end{array} \right\rbrace. \end{align*} $$
Exercise 6.6. Let
![]() $\vec {\gamma } := (\gamma _1,\ldots ,\gamma _k)$
be an ordered simple closed multi-curve on
$\vec {\gamma } := (\gamma _1,\ldots ,\gamma _k)$
be an ordered simple closed multi-curve on
![]() $S_g$
. Using Mirzakhani’s integration formulas gives an explicit expression for
$S_g$
. Using Mirzakhani’s integration formulas gives an explicit expression for
 $$ \begin{align*} M(\vec{\gamma},L) := \int_{\mathcal{M}_g} m(X,\vec{\gamma},L) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) \end{align*} $$
$$ \begin{align*} M(\vec{\gamma},L) := \int_{\mathcal{M}_g} m(X,\vec{\gamma},L) \thinspace d\widehat{\mu}_{\mathrm{wp}}(X) \end{align*} $$
in terms of Weil–Petersson volume polynomials and conclude that
![]() $M(\vec {\gamma },L)$
is a polynomial in L of degree
$M(\vec {\gamma },L)$
is a polynomial in L of degree
![]() $6g-6$
. Hint: Follow the same approach as in Exercise 5.5.
$6g-6$
. Hint: Follow the same approach as in Exercise 5.5.
Following Exercise 6.6, we define
Theorem 6.7. Let
![]() $X \in \mathcal {M}_g$
be a hyperbolic structure on
$X \in \mathcal {M}_g$
be a hyperbolic structure on
![]() $S_g$
and
$S_g$
and
![]() $\vec {\gamma } := (\gamma _1,\ldots ,\gamma _k)$
with
$\vec {\gamma } := (\gamma _1,\ldots ,\gamma _k)$
with
![]() $1 \leq k \leq 3g-3$
be an ordered simple closed multi-curve on
$1 \leq k \leq 3g-3$
be an ordered simple closed multi-curve on
![]() $S_g$
. Then, the following asymptotic formula holds:
$S_g$
. Then, the following asymptotic formula holds:
 $$ \begin{align*} \lim_{L \to \infty} \frac{m(X,\vec{\gamma},L)}{L^{6g-6}} = \frac{m(\vec{\gamma}) \cdot B(X)}{b_g}. \end{align*} $$
$$ \begin{align*} \lim_{L \to \infty} \frac{m(X,\vec{\gamma},L)}{L^{6g-6}} = \frac{m(\vec{\gamma}) \cdot B(X)}{b_g}. \end{align*} $$
In [Reference Arana-HerreraAra22], a generalization of Theorem 6.7 for ordered filling closed multi-curves was proved using techniques introduced by Mirzakhani in [Reference MirzakhaniMir16]. A result analogous to Theorem 6.7 for all topological types of closed curves has since been proved by Erlandsson and Souto using original methods [Reference Erlandsson and SoutoES22]. Theorem 6.7 was proved independently by the author [Reference Arana-HerreraAra22] and Liu [Reference LiuLiu22] using general averaging and unfolding arguments introduced by Margulis in his thesis [Reference MargulisMar70]. The main idea of the proof is to average over the moduli space of hyperbolic surfaces to reduce the original counting problem to an equidistribution problem for ‘horoballs’ in moduli space. This problem, in turn, can be studied using the ergodicity of the earthquake flow established by Mirzakhani in [Reference MirzakhaniMir08a].
6.7 Effective countings
The counting results discussed above only provide asymptotic estimates without explicit error terms. The search for effective estimates for counting problems of simple closed geodesics has only seen progress in recent years. In [Reference Eskin, Mirzakhani and MohammadiEMM22], Eskin, Mirzakhani, and Mohammadi introduced new methods fundamentally based on Teichmüller dynamics to prove the following effective version of Mirzakhani’s simple closed geodesic counting theorem.
Theorem 6.8. [Reference Eskin, Mirzakhani and MohammadiEMM22]
Let
![]() $X \in \mathcal {M}_g$
be a hyperbolic structure on
$X \in \mathcal {M}_g$
be a hyperbolic structure on
![]() $S_g$
and
$S_g$
and
![]() $\gamma := \sum _{i=1}^k a_i \gamma _i$
be an integral simple closed multi-curve on
$\gamma := \sum _{i=1}^k a_i \gamma _i$
be an integral simple closed multi-curve on
![]() $S_g$
. Then, for every
$S_g$
. Then, for every
![]() $L> 0$
,
$L> 0$
,
 $$ \begin{align*} s(X,\gamma,L) = \frac{c(\gamma) \cdot B(X)}{b_g} \cdot L^{6g-6} + O_{X,\gamma}(L^{6g-6-\kappa}), \end{align*} $$
$$ \begin{align*} s(X,\gamma,L) = \frac{c(\gamma) \cdot B(X)}{b_g} \cdot L^{6g-6} + O_{X,\gamma}(L^{6g-6-\kappa}), \end{align*} $$
where
![]() $\kappa = \kappa (g)> 0$
is a positive constant depending only on the genus
$\kappa = \kappa (g)> 0$
is a positive constant depending only on the genus
![]() $g \geq 2$
.
$g \geq 2$
.
Even more recently, in [Reference Arana-HerreraAra24], novel methods were introduced by the author to prove analogous effective estimates for countings of filling closed geodesics of a given topological type.
Theorem 6.9. [Reference Arana-HerreraAra24]
Let
![]() $X \in \mathcal {M}_g$
be a hyperbolic structure on
$X \in \mathcal {M}_g$
be a hyperbolic structure on
![]() $S_g$
and
$S_g$
and
![]() $\gamma $
be a filling closed curve on
$\gamma $
be a filling closed curve on
![]() $S_g$
. Then, for every
$S_g$
. Then, for every
![]() $L> 0$
,
$L> 0$
,
 $$ \begin{align*} f(X,\gamma,L) = \frac{c(\gamma) \cdot B(X)}{b_g} \cdot L^{6g-6} + O_{X,\gamma}(L^{6g-6-\kappa}), \end{align*} $$
$$ \begin{align*} f(X,\gamma,L) = \frac{c(\gamma) \cdot B(X)}{b_g} \cdot L^{6g-6} + O_{X,\gamma}(L^{6g-6-\kappa}), \end{align*} $$
where
![]() $\kappa = \kappa (g)> 0$
is a positive constant depending only on the genus
$\kappa = \kappa (g)> 0$
is a positive constant depending only on the genus
![]() $g \geq 2$
.
$g \geq 2$
.
Forthcoming work of Honaryar [Reference HonaryarHon24] extends the techniques introduced in [Reference Arana-HerreraAra24] to prove a version of Theorem 6.9 for non-simple, non-filling closed curves. The approach in [Reference Arana-HerreraAra24] is based on a so-called ‘tracking method’. The backbone of this method is a ‘tracking principle’ established in [Reference Arana-HerreraAra21], which, roughly speaking, shows that the action of the mapping class group on the space of closed curves of a closed surface effectively ‘tracks’ the corresponding action on Teichmüller space in the following sense: for all but quantitatively few mapping classes, the information of how a mapping class moves a given point of Teichmüller space determines, up to a power saving error term, how it changes the geometric intersection numbers of a given closed curve with respect to arbitrary geodesic currents. This principle allows one to reduce Theorem 6.9 to an effective orbit counting problem in Teichmüller space. This problem was studied in the prequel [Reference Arana-HerreraAra23] building on previous work of Athreya et al [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12], as we now explain.
6.8 Orbits in Teichmüller space
The minimal quasiconformal distortion among quasiconformal maps between marked hyperbolic surfaces is measured by the Teichmüller distance; this is a metric on Teichmüller space. Denote by
![]() $B_R(X) \subseteq \mathcal {T}_g$
the ball of radius
$B_R(X) \subseteq \mathcal {T}_g$
the ball of radius
![]() $R>0$
centered at
$R>0$
centered at
![]() $X \in \mathcal {T}_g$
with respect to the Teichmüller metric. Inspired by analogous results in homogeneous dynamics, see for instance [Reference Eskin and McMullenEM93], Athreya et al proved the following result in [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12].
$X \in \mathcal {T}_g$
with respect to the Teichmüller metric. Inspired by analogous results in homogeneous dynamics, see for instance [Reference Eskin and McMullenEM93], Athreya et al proved the following result in [Reference Athreya, Bufetov, Eskin and MirzakhaniABEM12].
Theorem 6.10. There exists a positive constant
![]() $C_g> 0$
such that for every
$C_g> 0$
such that for every
![]() $X,Y \in \mathcal {T}_g$
,
$X,Y \in \mathcal {T}_g$
,
Building on the work of Athreya et al, the author proved the following effective version of [Reference Arana-HerreraAra23, Theorem 6.10].
Theorem 6.11. There exists a positive constant
![]() $C_g> 0$
such that for every
$C_g> 0$
such that for every
![]() $X,Y \in \mathcal {T}_g$
,
$X,Y \in \mathcal {T}_g$
,
where
![]() $\kappa = \kappa (g)> 0$
is a positive constant depending only on the genus
$\kappa = \kappa (g)> 0$
is a positive constant depending only on the genus
![]() $g \geq 2$
.
$g \geq 2$
.
The main idea behind the proof of Theorem 6.10 can already be seen in some of the results discussed above. Following Margulis’s thesis [Reference MargulisMar70], it is possible to reduce Theorem 6.10 to a problem about equidistribution of Teichmüller metric balls on moduli space. This problem can, in turn, be studied using the exponential mixing property of the Teichmüller geodesic flow [Reference Avila and GouëzelAG13, Reference Avila, Gouëzel and YoccozAGY06, Reference Avila and ResendeAR12]. The effectivization of Theorem 6.10 in Theorem 6.11 requires a very fine analysis of the geometry and dynamics of Teichmüller space. Let us also highlight that the ‘tracking method’ discussed above can also be used to prove an effective version of Rafi and Souto’s asymptotic estimate for the number of points in a mapping class group orbit of Teichmüller space that lie within a ball of given center and large radius with respect to Thurston’s asymmetric metric [Reference Arana-HerreraAra24].
Acknowledgments
The author is very grateful to Alex Wright and Steve Kerckhoff for their invaluable advice, patience, and encouragement. The author would also like to thank Alex Wright, Anton Zorich, and Howard Masur for their helpful comments on an earlier version of this survey. This survey got started as a set of notes for a minicourse taught by the author at the CMI-HIMR Dynamics and Geometry Online Summer School. The author is very grateful to Viveka Erlandsson, John Mackay, and Jens Marklof for giving him the chance to teach this minicourse. This survey was finished while the author was a member of the Institute for Advanced Study (IAS). The author is very grateful to the IAS for its hospitality. This material is based upon work supported by the National Science Foundation under Grant No. DMS-1926686.