Let 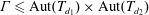$\unicode[STIX]{x1D6E4}\leqslant \text{Aut}(T_{d_{1}})\times \text{Aut}(T_{d_{2}})$ be a group acting freely and transitively on the product of two regular trees of degree 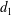$d_{1}$ and 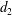$d_{2}$. We develop an algorithm that computes the closure of the projection of $\unicode[STIX]{x1D6E4}$ on 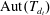$\text{Aut}(T_{d_{t}})$ under the hypothesis that 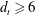$d_{t}\geqslant 6$ is even and that the local action of 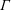$\unicode[STIX]{x1D6E4}$ on 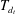$T_{d_{t}}$ contains 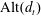$\text{Alt}(d_{t})$. We show that if 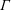$\unicode[STIX]{x1D6E4}$ is torsion-free and 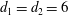$d_{1}=d_{2}=6$, exactly seven closed subgroups of 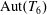$\text{Aut}(T_{6})$ arise in this way. We also construct two new infinite families of virtually simple lattices in 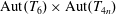$\text{Aut}(T_{6})\times \text{Aut}(T_{4n})$ and in 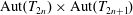$\text{Aut}(T_{2n})\times \text{Aut}(T_{2n+1})$, respectively, for all 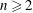$n\geqslant 2$. In particular, we provide an explicit presentation of a torsion-free infinite simple group on 5 generators and 10 relations, that splits as an amalgamated free product of two copies of 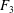$F_{3}$ over 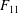$F_{11}$. We include information arising from computer-assisted exhaustive searches of lattices in products of trees of small degrees. In an appendix by Pierre-Emmanuel Caprace, some of our results are used to show that abstract and relative commensurator groups of free groups are almost simple, providing partial answers to questions of Lubotzky and Lubotzky–Mozes–Zimmer.