Any attempt to give “foundations”, for category theory or any domain in mathematics, could have two objectives, of course related.
(0.1) Noncontradiction: Namely, to provide a formal frame rich enough so that all the actual activity in the domain can be carried out within this frame, and consistent, or at least relatively consistent with a well-established and “safe” theory, e.g. Zermelo-Frankel (ZF).
(0.2) Adequacy, in the following, nontechnical sense:
(i) The basic notions must be simple enough to make transparent the syntactic structures involved.
(ii) The translation between the formal language and the usual language must be, or very quickly become, obvious. This implies in particular that the terminology and notations in the formal system should be identical, or very similar, to the current ones. Although this may seem minor, it is in fact very important.
(iii) “Foundations” can only be “foundations of a given domain at a given moment”, therefore the frame should be easily adaptable to extensions or generalizations of the domain, and, even better, in view of (i), it should suggest how to find meaningful generalizations.
(iv) Sometimes (ii) and (iii) can be incompatible because the current notations are not adapted to a more general situation. A compromise is then necessary. Usually when the tradition is very strong (ii) is predominant, but this causes some incoherence for the notations in the more general case (e.g. the notation f(x) for the value of a function f at x obliges one, in category theory, to denote the composition of arrows (f, g) → g∘f, and all attempts to change this notation have, so far, failed).
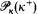 κ(κ+)
κ(κ+)