Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsubara, Yo
1987.
Menas' conjecture and generic ultrapowers.
Annals of Pure and Applied Logic,
Vol. 36,
Issue. ,
p.
225.
Abe, Yoshihiro
1988.
Weakly normal filters and the closed unbounded filter on 𝑃_{𝜅}𝜆.
Proceedings of the American Mathematical Society,
Vol. 104,
Issue. 4,
p.
1226.
Velic̆ković, Boban
1992.
Forcing axioms and stationary sets.
Advances in Mathematics,
Vol. 94,
Issue. 2,
p.
256.
Donder, Hans-Dieter
and
Matet, Pierre
1993.
Two cardinal versions of diamond.
Israel Journal of Mathematics,
Vol. 83,
Issue. 1-2,
p.
1.
Todorčević, Stevo
1993.
Finite and Infinite Combinatorics in Sets and Logic.
p.
385.
Velickovic, Boban
and
Woodin, W.Hugh
1998.
Complexity of reals in inner models of set theory.
Annals of Pure and Applied Logic,
Vol. 92,
Issue. 3,
p.
283.
Shioya, Masahiro
1999.
Splitting ρκλ into maximally many stationary sets.
Israel Journal of Mathematics,
Vol. 114,
Issue. 1,
p.
347.
Feng, Qi
2000.
Strongly baire trees and a Cofinal Branch Principle.
Israel Journal of Mathematics,
Vol. 117,
Issue. 1,
p.
71.
MATSUBARA, YO
and
SHELAH, SAHARON
2002.
NOWHERE PRECIPITOUSNESS OF THE NON-STATIONARY IDEAL OVER ${\mathcal P}_\kappa \lambda$.
Journal of Mathematical Logic,
Vol. 02,
Issue. 01,
p.
81.
Krueger, John
2005.
Destroying stationary sets.
Israel Journal of Mathematics,
Vol. 147,
Issue. 1,
p.
285.
Krueger, John
2006.
Adding clubs with square.
Annals of Pure and Applied Logic,
Vol. 141,
Issue. 1-2,
p.
1.
Harizanov, Valentina
2006.
2005–06 Winter Meeting of the Association for Symbolic Logic.
Bulletin of Symbolic Logic,
Vol. 12,
Issue. 4,
p.
613.
Usuba, Toshimichi
2007.
Local saturation of the non-stationary ideal over Pκλ.
Annals of Pure and Applied Logic,
Vol. 149,
Issue. 1-3,
p.
100.
Džamonja, Mirna
2007.
2007 Annual Meeting of the Association for Symbolic Logic.
Bulletin of Symbolic Logic,
Vol. 13,
Issue. 3,
p.
386.
Krueger, John
2009.
Some applications of mixed support iterations.
Annals of Pure and Applied Logic,
Vol. 158,
Issue. 1-2,
p.
40.
Jech, Thomas
2010.
Handbook of Set Theory.
p.
93.
Foreman, Matthew
2010.
Handbook of Set Theory.
p.
885.
Todorcevic, Stevo
2011.
Combinatorial Dichotomies in Set Theory.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 1,
p.
1.
Viale, Matteo
and
Weiß, Christoph
2011.
On the consistency strength of the proper forcing axiom.
Advances in Mathematics,
Vol. 228,
Issue. 5,
p.
2672.
Cox, Sean
and
Viale, Matteo
2013.
Martin’s Maximum and tower forcing.
Israel Journal of Mathematics,
Vol. 197,
Issue. 1,
p.
347.


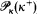
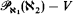 stationary
stationary