Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-22T15:54:52.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results concerning strongly compact cardinals

Published online by Cambridge University Press:  12 March 2014

Yoshihiro Abe
Yoshihiro Abe*
Affiliation:
Fukushima Technical College, Iwaki-City, Fukushima 970, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

This paper consists of two parts. In §1 we mention the first strongly compact cardinal. Magidor proved in [6] that it can be the first measurable and it can be also the first supercompact. In [2], Apter proved that Con(ZFC + there is a supercompact limit of supercompact cardinals) implies Con(ZFC + the first strongly compact cardinal κ is ϕ(κ)-supercompact + no α < κ is ϕ(α)-supercompact) for a formula ϕ which satisfies certain conditions.

We shall get almost the same conclusion as Apter's theorem assuming only one supercompact cardinal. Our notion of forcing is the same as in [2] and a trick makes it possible.

In §2 we study a kind of fine ultrafilter on Pκλ investigated by Menas in [7], where κ is a measurable limit of strongly compact cardinals. He showed that such an ultrafilter is not normal in some case (Theorems 2.21 and 2.22 in [7]). We shall show that it is not normal in any case (even if κ is supercompact). We also prove that it is weakly normal in some case.

We work in ZFC and much of our notation is standard. But we mention the following: the letters α,β,γ… denote ordinals, whereas κ,λ,μ,… are reserved for cardinals. R(α) is the collection of sets rank <α. φM denotes the realization of a formula φ to a class M. Except when it is necessary, we drop “M”. For example, M ⊩ “κ is φ(κ)-supercompact” means “κ is φM(κ)-supercompact in M”. If x is a set, |x| is its cardinality, Px is its power set, and 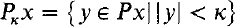. If also x ⊆ OR, 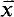denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “p < q” means “p is stronger than q”.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 4 , December 1985 , pp. 874 - 880
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abe, Y., Strongly compact cardinals, elementary embeddings and fixed points, this Journal, vol. 49 (1984), pp. 808–812.Google Scholar
[2]Apter, A. W., On the least strongly compact cardinal, Israel Journal of Mathematics, vol. 35 (1980), pp. 225–233.CrossRefGoogle Scholar
[3]Barbanel, J. B., Supercompact cardinals, elementary embeddings and fixed points, this Journal, vol. 47 (1982), pp. 84–88.Google Scholar
[4]Baumgartner, J. E., Iterated forcing, Proceedings of the Summer School in Set Theory, Cambridge, 1978 (Mathias, A. R. D., editor), London Mathematical Society Lecture Notes Series No. 87, Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
[5]Lévy, A. and Solovay, R. M., Measurable cardinals and the continuum hypothesis, Israel Journal of Mathematics, vol. 5 (1967), pp. 234–248.Google Scholar
[6]Magidor, M., How large is the first strongly compact cardinal?, Annals of Mathematical Logic, vol. 10 (1976) pp. 33–57.CrossRefGoogle Scholar
[7]Menas, T. K., On strong compactness and supercompactness, Annals of Mathematical Logic, vol. 7 (1974), pp. 327–359.CrossRefGoogle Scholar
[8]Menas, T. K., Consistency results concerning supercompactness, Transactions of the American Mathematical Society, vol. 223 (1976), pp. 61–91.Google Scholar
[9]Shoenfield, J. R., Unramified forcing, Axiomatic Set Theory, Proceedings of Symposia in Pure Mathematics, vol. 13, Part I (Scott, D., editor), American Mathematical Society, Providence, Rhode Island, 1971, pp. 357–381.CrossRefGoogle Scholar
[10]Solovay, R. M., Strongly compact cardinals and the G.C.H., Proceedings of the Tarski Symposium, Proceedings of Symposia in Pure Mathematics, vol. 25 (Henkin, L., editor), American Mathematical Society, Providence, Rhode Island, 1974, pp. 365–372.CrossRefGoogle Scholar
[11]Solovay, R. M., Reinhardt, W. N. and Kanamori, A., Strong axioms of infinity and elementary embeddings, Annals of Mathematical Logic, vol. 13 (1978), pp. 73–116.CrossRefGoogle Scholar