Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-31T13:34:10.296Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of generators of cylindric algebras

Published online by Cambridge University Press:  12 March 2014

H. Andréka  and
I. Németi
H. Andréka
Affiliation:
Mathematical Institute, Hungarian Academy of Sciences, Budapest, Hungary
I. Németi
Affiliation:
Mathematical Institute, Hungarian Academy of Sciences, Budapest, Hungary
Get access Rights & Permissions [Opens in a new window]

Extract

The theory of cylindric algebras (CA's) is the algebraic theory of first order logics. Several ideas about logic are easier to formulate in the frame of CA-theory. Such are e.g. some concepts of abstract model theory (cf. [1] and [10]–[12]) as well as ideas about relationships between several axiomatic theories of different similarity types (cf. [4] and [10]). In contrast with the relationship between Boolean algebras and classical propositional logic, CA's correspond not only to classical first order logic but also to several other ones. Hence CA-theoretic results contain more information than their counterparts in first order logic. For more about this see [1], [3], [5], [9], [10] and [12].

Here we shall use the notation and concepts of the monographs Henkin-Monk-Tarski [7] and [8]. ω denotes the set of natural numbers. CAα denotes the class of all cylindric algebras of dimension α; by “a CAα” we shall understand an element of the class CAα. The class Dcα ⊆ CAα was defined in [7]. Note that Dcα = 0 for α ∈ ω. The classes Wsα, 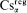and Csα were defined in 1.1.1 of [8], p. 4. They are called the classes of all weak cylindric set algebras, regular cylindric set algebras and cylindric set algebras respectively. It is proved in [8] (I.7.13, I.1.9) that 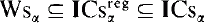⊆ CAα. (These inclusions are proper by 7.3.7, 1.4.3 and 1.5.3 of [8].)

It was proved in 2.3.22 and 2.3.23 of [7] that every simple, finitely generated Dcα is generated by a single element. This is the algebraic counterpart of a property of first order logics (cf. 2.3.23 of [7]). The question arose: for which simple CAα's does “finitely generated” imply “generated by a single element” (see p. 291 and Problem 2.3 in [7]). In terms of abstract model theory this amounts to asking the question: For which logics does the property described in 2.3.23 of [7] hold? This property is roughly the following. In any maximal theory any finite set of concepts is definable in terms of a single concept. The connection with CA-theory is that maximal theories correspond to simple CA's (the elements of which are the concepts of the original logic) and definability corresponds to generation.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 4 , December 1985 , pp. 865 - 873
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andréka, H., Gergely, T. and Németi, I., On universal algebraic constructions of logics, Studia Logica, vol. 36 (1977), pp. 9–47.CrossRefGoogle Scholar
[2]Andréka, H. and Németi, I., Which finite cylindric algebras are generated by a single element?Finite algebra and multiple-valued logic (Proceedings of the Colloquium, Szeged, 1979), Colloquia Mathematica Societatis Janos Bolyai, vol. 28, North-Holland, Amsterdam, 1981, pp. 23–39.Google Scholar
[3]Andréka, H. and Sain, I., Connections between algebraic logic and initial algebra semantics of CF languages, Mathematical logic in computer science (Papers from the Colloquium, Salgótarjan, 1978), Colloquia Mathematica Societatis János Bolyai, vol. 26, North-Holland, Amsterdam, 1981, pp. 25–83.Google Scholar
[4]Burstall, R. M. and Goguen, J. A., Putting theories together to make specifications, Proceedings of the Fifth International Joint Conference on Artificial Intelligence (Cambridge, Massachusetts, 1977), Vol. 2, Department of Computer Science, Carnegie-Mellon University, Pittsburgh, Pennsylvania, 1977, pp. 1045–1058.Google Scholar
[5]Comer, S. D., Review of [1], Mathematical Reviews, vol. 58 (1979), #21599.Google Scholar
[6]Henkin, L. and Monk, J. D., Cylindric algebras and related structures, Proceedings of the Tarski Symposium, Proceedings of Symposia in Pure Mathematics, vol. 25, American Mathematical Society, Providence, Rhode Island, 1974, pp. 105–121.CrossRefGoogle Scholar
[7]Henkin, L., Monk, J. D. and Tarski, A., Cylindric algebras. Parts I, II, North-Holland, Amsterdam, 1971, 1985.Google Scholar
[8]Henkin, L., Monk, J. D., Tarski, A., Andréka, H. and Németi, I., Cylindric set algebras, Lecture Notes in Mathematics, vol. 883, Springer-Verlag, Berlin, 1981.CrossRefGoogle Scholar
[9]Németi, I., Some constructions of cylindric algebra theory applied to dynamic algebras of programs, CL&CL—Computational Linguistics and Computer Languages, vol. 14 (1980), pp. 43–65.Google Scholar
[10]Németi, I., Connections between cylindric algebras and initial algebra semantics of CF languages, Mathematical logic in computer science (Papers from the Colloquium, Salgótarján, 1978), Colloquia Mathematica Societatis János Bolyai, vol. 26, North-Holland, Amsterdam, 1981, pp. 561–605.Google Scholar
[11]Sain, I., There are general rules for specifying semantics: Observations on abstract model theory, CL&CL—Computational Linguistics and Computer Languages, vol. 13 (1979), pp. 195–250.Google Scholar
[12]Sain, I., Improving a theorem of Andréka, Monk and Németi in cylindric algebric model theory, Notre Dame Journal of Formal Logic (to appear).Google Scholar