No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Before stating the results we would like to thank the referee for reorganizing the whole paper and changing its original logical terminology to an algebraical terminology.
Let Z* be a proper elementary extension of the integral domain Z. For any b ∈ Z*∖Z we define Z〈b〉 as the following subring of Z*:
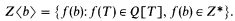
It is easy to prove that the natural divisibility relation on Z〈b〉 is the restriction to Z〈b〉 of the divisibility on Z* (see Lemma 1.1 below). The much stronger statement that Z〈b〉 is algebraically closed in Z* does not hold for all b. Similarly, there are many b's such that Z〈b〉 is not a recursive ring, e.g. if the set of standard primes dividing b is not recursive then Z〈b〉 cannot be a recursive ring under any bijection with N.
Our main result is the following.
Theorem. There exists an element b ∈ Z*∖Z such that
(1) Z〈b〉 is algebraically closed in Z*,
(2) Z〈b〉 is a recursive ring, and
(3) each infinite element of Z〈b〉 is divisible by a standard integer > 1 (so the only “primes” of Z〈b〉 are the standard ones).
An easy consequence of (1) is that certain induction axioms are satisfied by Z〈b〉. This explains the title of the paper. In the last section of the paper, §3, we shall say more about this.