Published online by Cambridge University Press: 12 March 2014
Let M be a term of the type free λ-calculus and let 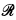 be a set of occurrences of redexes in M. A reduction sequence from M which first contracts a member of
be a set of occurrences of redexes in M. A reduction sequence from M which first contracts a member of 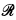 and afterwards only residuals of
and afterwards only residuals of 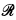 is called a development (of M with respect to
is called a development (of M with respect to 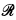 ). The finite developments theorem says that developments are always finite.
). The finite developments theorem says that developments are always finite.
There are several proofs of this theorem in the literature. A plausible strategy is to define some kind of measure for pairs (M, 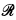 ), which—if M′ results from M by contracting a redex occurrence in
), which—if M′ results from M by contracting a redex occurrence in 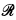 and
and 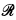 ′ is the set of residuals of
′ is the set of residuals of 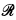 in M′— decreases in passing from (M,
in M′— decreases in passing from (M, 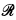 ) to (M′,
) to (M′, 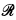 ′). This procedure is followed as a matter of fact in the proofs in Hyland [4] and in Barendregt [1] (both are covered in Klop [5]). If, as in the latter proof, the natural numbers are used as measures, then the measure of (M,
′). This procedure is followed as a matter of fact in the proofs in Hyland [4] and in Barendregt [1] (both are covered in Klop [5]). If, as in the latter proof, the natural numbers are used as measures, then the measure of (M, 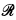 ) will actually denote an upper bound of the number of reduction steps in a development of M with respect to
) will actually denote an upper bound of the number of reduction steps in a development of M with respect to 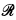 .
.
In the present proof we straightforwardly define for each pair (M, 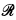 ) a natural number, which can easily be seen to indicate the exact number of reduction steps in a development of maximal length of M with respect to
) a natural number, which can easily be seen to indicate the exact number of reduction steps in a development of maximal length of M with respect to 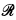 .
.