We prove that every infinite-dimensional Banach space $X$ having a (not necessarily equivalent) real-analytic norm is real-analytic diffeomorphic to $X\,\backslash \,\left\{ 0 \right\}$. More generally, if $X$ is an infinite dimensional Banach space and $F$ is a closed subspace of $X$ such that there is a real-analytic seminorm on $X$ whose set of zeros is $F$, and $X/F$ is infinite-dimensional, then $X$ and $X\backslash F$ are real-analytic diffeomorphic. As an application we show the existence of real-analytic free actions of the circle and the $n$-torus on certain Banach spaces.

The Cuntz-Krieger algebra ${{\mathcal{O}}_{B}}$ is defined for an arbitrary, possibly infinite and infinite valued, matrix $B$. A graph ${{C}^{*}}$-algebra ${{G}^{*}}\left( E \right)$ is introduced for an arbitrary directed graph $E$, and is shown to coincide with a previously defined graph algebra ${{C}^{*}}\left( E \right)$ if each source of $E$ emits only finitely many edges. Each graph algebra ${{G}^{*}}\left( E \right)$ is isomorphic to the Cuntz-Krieger algebra ${{\mathcal{O}}_{B}}$ where $B$ is the vertex matrix of $E$.

Si $M$ est une variété de dimension $n$, compacte non simplement connexe, on caractérise les métriques riemanniennes sur $M$ dont la fonction croissance a exactement deux singularités.

In this paper we study simple associative algebras with finite $\mathbb{Z}$-gradings. This is done using a simple algebra ${{F}_{g}}$ that has been constructed in Morita theory from a bilinear form $g:\,U\,\times \,V\,\to \,A$ over a simple algebra $A$. We show that finite $\mathbb{Z}$-gradings on ${{F}_{g}}$ are in one to one correspondence with certain decompositions of the pair $\left( U,\,V \right)$. We also show that any simple algebra $R$ with finite $\mathbb{Z}$-grading is graded isomorphic to ${{F}_{g}}$ for some bilinear from $g:\,U\,\times \,V\,\to \,A$, where the grading on ${{F}_{g}}$ is determined by a decomposition of $\left( U,\,V \right)$ and the coordinate algebra $A$ is chosen as a simple ideal of the zero component ${{R}_{0}}$ of $R$. In order to prove these results we first prove similar results for simple algebras with Peirce gradings.

Langlands has conjectured the existence of a universal group, an extension of the absolute Galois group, which would play a fundamental role in the classification of automorphic representations. We shall describe a possible candidate for this group. We shall also describe a possible candidate for the complexification of Grothendieck's motivic Galois group.

For a modular elliptic curve $E/\mathbb{Q}$, we show a number of links between the primes $\ell $ for which the mod $\ell $ representation of $E/\mathbb{Q}$ has projective dihedral image and congruence primes for the newform associated to $E/\mathbb{Q}$.

In this paper we extend a well-known theorem of M. Scheunert on skew-symmetric bicharacters of groups to the case of skew-symmetric bicharacters on arbitrary cocommutative Hopf algebras over a field of characteristic not 2. We also classify polycharacters on (restricted) enveloping algebras and bicharacters on divided power algebras.

We explicitly describe, in terms of indecomposable ${{\mathbb{Z}}_{2}}\left[ G \right]$-modules, the Galois module structure of ideals in totally ramified biquadratic extensions of local number fields with only one break in their ramification filtration. This paper completeswork begun in [Elder: Canad. J.Math. (5) 50(1998), 1007–1047].

If an operator $T$ satisfies a modular inequality on a rearrangement invariant space ${{L}^{\rho}}\left( \Omega ,\mu \right)$, and if $p$ is strictly between the indices of the space, then the Lebesgue inequality $\int{|Tf{{|}^{P}}\le C\int{|f{{|}^{P}}}}$ holds. This extrapolation result is a partial converse to the usual interpolation results. A modular inequality for Orlicz spaces takes the form $\int{\Phi \left( |Tf| \right)\le }\int{\Phi \left( C|f| \right)}$, and here, one can extrapolate to the (finite) indices $i\left( \Phi \right)$ and $I\left( \Phi \right)$ as well.

It is known that the $K$-groups that appear in the calculation of the $K$-theory of a large class of groups can be computed from the $K$-theory of their virtually infinite cyclic subgroups. On the other hand, Nil-groups appear to be the obstacle in calculations involving the $K$-theory of the latter. The main difficulty in the calculation of Nil-groups is that they are infinitely generated when they do not vanish. We develop methods for computing the exponent of $\text{N}{{\text{K}}_{0}}$-groups that appear in the calculation of the ${{K}_{0}}$-groups of virtually infinite cyclic groups.

Let 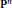${{\mathbf{P}}^{n}}$ be the $n$-dimensional projective space over some algebraically closed field $k$ of characteristic 0. For an integer 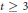$t\,\ge \,3$ consider the invertible sheaf 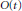$O\left( t \right)$ on 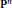${{\mathbf{P}}^{n}}$ (Serre twist of the structure sheaf). Let 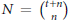$N\,=\,\left( \underset{n}{\mathop{t+n}}\, \right)$, the dimension of the space of global sections of 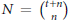$O\left( t \right)$, and let $k$ be an integer satisfying 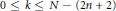$0\,\le \,k\,\le \,N\,-\,\left( 2n\,+\,2 \right)$. Let 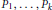${{P}_{1}},\ldots ,{{P}_{k}}$ be general points on 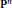${{\mathbf{P}}^{n}}$ and let 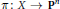$\pi :\,X\,\to \,{{\mathbf{P}}^{n}}$ be the blowing-up of 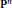${{\mathbf{P}}^{n}}$ at those points. Let 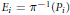${{E}_{i}}\,=\,{{\pi }^{-1}}\left( {{P}_{i}} \right)$ with 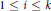$1\,\le \,i\,\le \,k$ be the exceptional divisor. Then 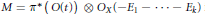$M={{\pi }^{*}}\left( O(t) \right)\,\otimes \,{{O}_{X}}\left( -{{E}_{1}}-\cdots -{{E}_{k}} \right)$ is a very ample invertible sheaf on 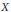$X$.

A Dirac comb of point measures in Euclidean space with bounded complex weights that is supported on a lattice $\Gamma$ inherits certain general properties from the lattice structure. In particular, its autocorrelation admits a factorization into a continuous function and the uniformlattice Dirac comb, and its diffraction measure is periodic, with the dual lattice ${{\Gamma }^{*}}$ as lattice of periods. This statement remains true in the setting of a locally compact Abelian group whose topology has a countable base.

Let $G$ be a discrete subgroup of $\text{SL}\left( 2,\,\mathbb{R} \right)$ which contains $\Gamma \left( N \right)$ for some $N$. If the genus of $X\left( G \right)$ is zero, then there is a unique normalised generator of the field of $G$-automorphic functions which is known as a normalised Hauptmodul. This paper gives a characterisation of normalised Hauptmoduls as formal $q$ series using modular polynomials.

We prove that the Mahler measure of an algebraic number cannot be too close to an integer, unless we have equality. The examples of certain Pisot numbers show that the respective inequality is sharp up to a constant. All cases when the measure is equal to the integer are described in terms of the minimal polynomials.

On explicite une classe de champ de vecteurs polynomiaux non analytiquement linéarisables à l'aide de la correction introduite par Écalle-Vallet. Notamment, on étend des résultats de Schuman sur la trivialité des hamiltoniens homogàenes isochrones.

Let $\Phi $ be an algebraically closed field of characteristic zero, $G$ a finite, not necessarily abelian, group. Given a $G$-grading on the full matrix algebra $A\,=\,{{M}_{n}}\left( \Phi \right)$, we decompose $A$ as the tensor product of graded subalgebras $A\,=\,B\,\otimes \,C,\,B\,\cong \,{{M}_{p}}\left( \Phi \right)$ being a graded division algebra, while the grading of $C\,\cong \,{{M}_{q}}\left( \Phi \right)$ is determined by that of the vector space ${{\Phi }^{n}}$. Now the grading of $A$ is recovered from those of $A$ and $B$ using a canonical “induction” procedure.

In this note we show that for an arbitrary reductive Lie group and any admissible irreducible Banach representation the Mellin transforms of Whittaker functions extend to meromorphic functions. We locate the possible poles and show that they always lie along translates of walls of Weyl chambers.

We compute the rational Chow groups of supersingular abelian varieties and some other related varieties, such as supersingular Fermat varieties and supersingular $K3$ surfaces. These computations are concordant with the conjectural relationship, for a smooth projective variety, between the structure of Chow groups and the coniveau filtration on the cohomology.

We determine the Lie superalgebras that are graded by the root systems of the basic classical simple Lie superalgebras of type $C\left( n \right),D\left( m,n \right),D\left( 2,1;\alpha \right)\left( \alpha \in \mathbb{F}\backslash \left\{ 0,-1 \right\} \right),F(4)$, and $G(3)$.

A local version of $\text{VMO}$ is defined, and the local Hardy space ${{h}_{1}}$ is shown to be its dual. An application to weak-$*$ convergence in ${{h}_{1}}$ is proved.