Order-of-magnitude results are extended to the case of general second-order term, with coefficient not necessarily of fixed sign, with general positive weight-function. The bounds are used to establish the expression for the Titchmarsh–Weyl function m(λ) as a Nevanlinna function in terms of the spectral function.

The inequality (0·1) below is naturally associated with the equation −(pu′)′ + qu = λu. By assuming that one end-point of the interval (a, b) is regular and the other limit-point for this equation, Everitt characterized the best constant K in tems of spectral properties of the equation. This paper sketches a theory for more general inequalities (0·2), (0·3) similarly related to the equation Su = λTu. Here S and T are ordinary, symmetric differential expressions. A characterization of the best constants in (0·2), (0·3) is given which generalises that of Everitt.

For the case when S is of order 1 and T is multiplication by a positive function, all possible inequalities are given together with the best constants and cases of equality. Furthermore, an example is given of a valid inequality (0·1) on an interval with both end-points regular for the corresponding differential equation. This contradicts a conjecture by Everitt and Evans. Finally, the general theory for the left-definite inequality (0·3) is specialised to the case when S is a Sturm-Liouville expression. A family of examples is given for which the best constants can be explicitly calculated.

We discuss steady-state solutions of systems of semilinear reaction-diffusion equations which model situations in which two interacting species u and v inhabit the same bounded region. It is easy to find solutions to the systems such that either u or v is identically zero; such solutions correspond to the case where one of the species is extinct. By using decoupling and global bifurcation theory techniques, we prove the existence of solutions which are positive in both u and v corresponding to the case where the populations can co-exist.

A group 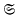consisting of real continuous functions of one real variable on the interval j = (−∞, ∞) is called planar if through each point of the plane j × j there passes just one element s ∈ .

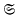Every differential oscillatory equation (Q): y″ = Q(t)y (t ∈ j = (−∞, ∞), Q ∈ C(0)) admits functions, called the dispersions of (Q), that transform (Q) into itself. These dispersions are integrals of Kummer's equation (QQ): −{X, t} + Q(X)X′2(t) = Q(t) and form a three-parameter group 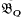, known as the dispersion group of (Q). The increasing dispersions of (Q) form a three-parameter group 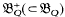invariant in 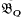. The centre of the group 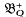is an infinite cyclic group 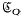, whose elements, the central dispersions of (Q), describe the position of conjugate points of (Q).

The present paper contains new results concerning the algebraic structure of the group 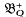. It provides information on the following: (1) the existence and properties of planar subgroups of a given group 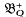and (2) the existence and properties of the groups 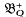containing a given planar group 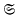. The results obtained are: the planar subgroups of a given group 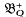form a system depending on two constants, SQ, such that 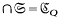for all 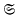∈SQ. The equations (Q) whose groups 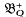contain the given planar group 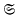form a system dependent on one constant, QS, such that for all (Q)∈QS.

Asymptotic approximations to solutions of perturbations of Meijer's differential equation are derived. These are used to determine deficiency indices for certain subspaces associated with related pairs of symmetric differential expressions.

For the differential equation Lf = λMf on an open interval of ℝ, a theory in terms of relations in a Hilbert space associated with M was developed in a paper by Coddington and de Snoo, and eigenfunction expansions were derived in a paper by Dijksma and de Snoo. In the case of a regular problem on a compact interval, pointwise convergence of the expansions was shown in another paper by Coddington and de Snoo. Here, we show pointwise convergence in the general singular case.

Let A be a product of symmetric matrices, A = RQ, with R non-singular, and let v be an eigenvector of A. For certain R and Q, a convenient formula for the expression (R−1v)tv is obtained. This expression occurs in the diagonalization of A and, in the particular case where A is associated with the quasi-derivative formulation of higher-order differential equations, the expression occurs in the asymptotic theory of solutions of the differential equation.

Let L0, M0 be closed densely defined linear operators in a Hilbert space H which form an adjoint pair, i.e. . In this paper, we study closed operators S which satisfy and are regularly solvable in the sense of Višik. The abstract results obtained are applied to operators generated by second-order linear differential expressions in a weighted space L2(a, b; w).

The components of a two (complex) dimensional Dirac system are studied as trajectories in the complex plane. The system, defined on an interval [a, b) of regular points, is assumed to be of limit circle type at t = b, and to be non-oscillatory there. By introducing moduli ρ1(t) = |y1(t)|, ρ2(t) = |y2(t)| and continuous complex arguments θ1(t) = arg y1(t), θ2(t) = arg y2(t) for the components, the principal result proved is that θ1(t) and θ2(t) are bounded as t → b. Examples show that monotonicity of the argument function θ1(t), which is a feature of the corresponding problem for Sturm–Liouville equations, fails for Dirac systems.

We consider ihe differential expression M[y]: = −y″ + qy on [0, ∞) where q_∈ Lp [0, ∞) for some p ≧ 1. It is known that M, together with the boundary conditions y(0) = 0 or y′(0) = 0, defines linear operators on L2 [0, ∞). We obtain lower bounds for the spectra of these operators. Our bounds depend on the Lp norm of q_ and extend results of Everitt and Veling.

This paper considers the asymptotic form, as λ tends to infinity in sectors omitting the real axis, of the matrix Titchmarsh-Weyl coefficient M(λ) for the fourth order equation y(4) + q(x)y = λy, where q(x) is real and locally absolutely integrable. By letting M0(λ) denote the m-coefficient for the Fourier case y(4) = λy, the asymptotic formula M(λ) = M0(λ) + 0(1) is established.

For β > β0: = 1 −[(n − 2)/2]2 and n ≧ 2, it was recently shown by Simon that the self-adjoint operator associated with −Δ + βr−2 in L2(ℝn) has domain H2(ℝn) ∩D(r−2) the constant β0 being the best possible. An alternative proof of this result is given.

Let , with each pi a finite sum of real multiples of real powers of x, and with D = d/dx. Suppose that pi≧0, pN > 0, and p0≧ε > 0 on the interval [1, ∞). Suppose that there exists a j such that degree pi − 2j > degree pi−2i for all i ≠ j. We compute the deficiency index d(Ln) in L2[l, ∞) of any power of L. It is known that d(L) = N. We give an exact formula for d(Ln) which, if degree pi − 2j > 0, shows that d(Ln) = nN for all n if and only if j = 0, and that the limit as n approaches infinity of d(Ln)/n is N + j. We show in addition that if degree pi − 2i ≦ 0 for all i, d(Ln) = nN for all n.

The inequality of Ganelius states that, for suitable functions f and g on an interval [a, b], [inf f + var f]sup ∫ jdg, where the supremum is taken over all sub-intervals J of [a, b]. A more general version of this inequality is derived as well as certain related generalized mean-value theorems.

Let the values of F be convex compact subsets of Rn and let F be upper semicontinuous with respect to x. There are two ways known of replacing F by a more regular map so that the set of solutions of (2) remains unchanged. We prove that both ways lead to the same more regular map and extend the results to the case where Rn is replaced by a separable Banach space.

Landau's inequality ∥y′∥2≦4∥y∥∥y″∥ is extended to ∥y′∥2≦K(a)∥y∥1−a ∥y″ ∣y∣a∥, K(a) = 4/(l−a), 0≦ a<1. The proof is elementary and new even in the case a = 0 considered by Landau.

For a symmetric linear relation S with a directing mapping, the notion of a spectral function is defined by means of a Bessel–Parseval inequality, and a description of all such spectral functions is given. As an application, we describe the set of all spectral functions of a canonical regular first order differential system.

Denote by (αj, βj), j = 1, 2, … an infinite set of disjoint open intervals on the half-line (0, ∞). Suppose that the following conditions are fulfilled:

With the aid of the first two trace formula presented earlier by the author, we prove in this paper that there exists a function q, defined on the whole real line, such that for the Schrödinger equation −y″ + q(x)y = λy (−∞<x<∞), the intervals (αj, βj) are spectrum lacunae. As an example, we consider the case when the intervals (αj, βj) are adjacent intervals of the Cantor trinary perfect set.

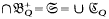An inequality whose origins date to the work of G. H. Hardy is presented. This Hardy-type inequality applies to derivatives of arbitrary order of functions whose domain is a subset of ℝn. The Friedrichs inequality is a corollary. The result is then used to establish lower bounds on the essential spectra of even-order elliptic partial differential operators on unbounded domains.