Published online by Cambridge University Press: 14 November 2011
Let 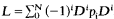 , with each pi a finite sum of real multiples of real powers of x, and with D = d/dx. Suppose that pi≧0, pN > 0, and p0≧ε > 0 on the interval [1, ∞). Suppose that there exists a j such that degree pi − 2j > degree pi−2i for all i ≠ j. We compute the deficiency index d(Ln) in L2[l, ∞) of any power of L. It is known that d(L) = N. We give an exact formula for d(Ln) which, if degree pi − 2j > 0, shows that d(Ln) = nN for all n if and only if j = 0, and that the limit as n approaches infinity of d(Ln)/n is N + j. We show in addition that if degree pi − 2i ≦ 0 for all i, d(Ln) = nN for all n.
, with each pi a finite sum of real multiples of real powers of x, and with D = d/dx. Suppose that pi≧0, pN > 0, and p0≧ε > 0 on the interval [1, ∞). Suppose that there exists a j such that degree pi − 2j > degree pi−2i for all i ≠ j. We compute the deficiency index d(Ln) in L2[l, ∞) of any power of L. It is known that d(L) = N. We give an exact formula for d(Ln) which, if degree pi − 2j > 0, shows that d(Ln) = nN for all n if and only if j = 0, and that the limit as n approaches infinity of d(Ln)/n is N + j. We show in addition that if degree pi − 2i ≦ 0 for all i, d(Ln) = nN for all n.