A group 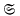consisting of real continuous functions of one real variable on the interval j = (−∞, ∞) is called planar if through each point of the plane j × j there passes just one element s ∈ .

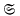Every differential oscillatory equation (Q): y″ = Q(t)y (t ∈ j = (−∞, ∞), Q ∈ C(0)) admits functions, called the dispersions of (Q), that transform (Q) into itself. These dispersions are integrals of Kummer's equation (QQ): −{X, t} + Q(X)X′2(t) = Q(t) and form a three-parameter group 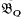, known as the dispersion group of (Q). The increasing dispersions of (Q) form a three-parameter group 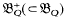invariant in 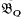. The centre of the group 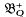is an infinite cyclic group 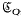, whose elements, the central dispersions of (Q), describe the position of conjugate points of (Q).

The present paper contains new results concerning the algebraic structure of the group 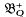. It provides information on the following: (1) the existence and properties of planar subgroups of a given group 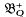and (2) the existence and properties of the groups 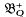containing a given planar group 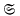. The results obtained are: the planar subgroups of a given group 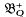form a system depending on two constants, SQ, such that 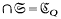for all 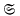∈SQ. The equations (Q) whose groups 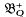contain the given planar group 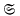form a system dependent on one constant, QS, such that 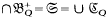for all (Q)∈QS.