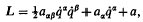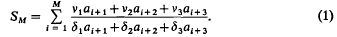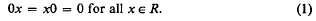Research Article
On Pták's double-limit theorems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 193-200
-
- Article
-
- You have access
- Export citation
Stability theorems for wedges
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 201-214
-
- Article
-
- You have access
- Export citation
Ideals in pseudo-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 215-222
-
- Article
-
- You have access
- Export citation
Products of idempotents in certain semigroups of transformations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 223-236
-
- Article
-
- You have access
- Export citation
The power inequality on normed spaces
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 237-240
-
- Article
-
- You have access
- Export citation
Integrals of dynamical systems linear in the velocities
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 241-244
-
- Article
-
- You have access
- Export citation
A remark on continuous bilinear mappings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 245-248
-
- Article
-
- You have access
- Export citation
Operator norms determined by their numerical ranges
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 249-255
-
- Article
-
- You have access
- Export citation
Inequalities for certain cyclic sums
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 257-262
-
- Article
-
- You have access
- Export citation
On uniqueness of flows of a dipolar fluid
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 263-269
-
- Article
-
- You have access
- Export citation
Varieties and d.g. near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 271-274
-
- Article
-
- You have access
- Export citation
On a conjecture of Guinand for the plane partition function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 275-276
-
- Article
-
- You have access
- Export citation
Articles
The osculating of a certain curve in [4]
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 277-280
-
- Article
-
- You have access
- Export citation
Research Article
The asymptotic expansion of the number of tree-like polyhexes†
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 281-282
-
- Article
-
- You have access
- Export citation
Book Reviews
P. Rosenstiehl, and J. Mothes, Mathematics in Management, translated from the French by MrsA. Silvey (North Holland Publishing, Co., Amsterdam, 1968), xvi+392 pp.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 283-284
-
- Article
-
- You have access
- Export citation
C. G. Lekkerkerker, Geometry of Numbers (North-Holland Publishing Company, 1969), 510 pp, 210s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 284
-
- Article
-
- You have access
- Export citation
B. L. van der Waerden, Mathematical Statistics (George Allen & Unwin Ltd., 1969), xi+367 pp., £7, 7s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 284-285
-
- Article
-
- You have access
- Export citation
A. Ogg, Modular Forms and Dirichlet Series (W. A. Benjamin, Inc., New York, 1969), xviii+173 pp., cloth $15, paper $6.95.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 285-286
-
- Article
-
- You have access
- Export citation
Martin Eisen, Elementary Combinatorial Analysis (Gordon and Breach, 1969), x+233 pp., 145s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 286
-
- Article
-
- You have access
- Export citation
John Milnor, Singular Points of Complex Hypersurfaces (Annals of Mathematics Studies, no. 61, Princeton University Press. London: Oxford University Press, 1969) 30s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 286
-
- Article
-
- You have access
- Export citation

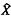 × Ŷ, where
× Ŷ, where 
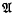 = (
= (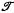 , one of the results being that if
, one of the results being that if