Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-19T05:06:26.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals of dynamical systems linear in the velocities

Published online by Cambridge University Press:  20 January 2009

C. D. Collinson
C. D. Collinson
Affiliation:
Department of Applied Mathematics, The University, Hull
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kilmister (1) has discussed the existence of linear integrals of a dynamical system specified by generalized coordinates qα(α = 1, 2, …, n) and a Lagrangian

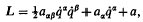
repeated indices being summed from 1 to n. He derived covariant conditions for the existence of such an integral, conditions which do not imply the existence of an ignorable coordinate. Boyer (2) discussed the conditions and found the most general Lagrangian satisfying the conditions for the case of two degrees of freedom (n = 2).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 17 , Issue 3 , June 1971 , pp. 241 - 244
Copyright
Copyright © Edinburgh Mathematical Society 1971

References

REFERENCES

(1)Kilmister, C. W., The existence of integrals of dynamical systems linear in the velocities, Edinburgh Math. Notes 44 (1961), 13–16, in Proc. Edinburgh Math. Soc. (2) 12 (1960–1961).CrossRefGoogle Scholar
(2)Boyer, R. H., On Kilmister's conditions for the existence of linear integrals of dynamical systems, Proc. Edinburgh Math. Soc. 14 (1964), 243–244.CrossRefGoogle Scholar
(3)Birkhoff, G. D., Dynamical Systems (New York, 1927), p. 44.Google Scholar
(4)Eisenhart, L. P., Riemannian Geometry (Princeton University Press, 1925), p. 230.Google Scholar